肋片形式对Hampson型换热器流动换热特性影响
王悠悠,文 键,张 星,王斯民,厉彦忠
(1.西安交通大学 能源与动力工程学院,西安 710049;2.西安交通大学 化学工程与技术学院,西安 710049)
0 引言
微型Hampson节流制冷机利用实际气体的焦耳-汤姆逊节流效应进行降温制冷,由于其结构简单紧凑且无运动部件、降温区间大、启动时间短等特点被广泛地应用于电子器件冷却。其主要结构包括高压储气瓶、Hampson型逆流换热器、节流装置、芯轴及外壳。制冷过程中,高压气体流经换热器肋片管管程,经过节流装置降温冷却后再通过肋片管与壳体的间隙返回冷却管[1]。Hampson型换热器承担着返流气体冷能回收、节流前气体预冷的重要任务,其性能优劣直接影响制冷机的整体性能。
Ng等[2]对使用氩作为工质的Hampson型节流制冷器的稳态特性进行了实验研究和一维数值计算,计算过程中实时更新节点物性数据,数值计算结果与实验数据吻合程度高;Chua等[3]采用一维数值计算结果的方式研究了Hampson型肋片管换热器,创新性地考虑了毛细管阻塞的影响;Ardhapurkar等[4]用Matlab软件建立了Hampson型节流制冷机的数值模型,将数值计算结果与Ng等的实验数据进行了对比;刘鑫等[5]基于有限差分法,考虑了流道形状、物性变化、轴向漏热及辐射漏热损失,模拟误差较小,他们还对换热器进行了多参数优化;肖日仕[6]对Hampson型节流制冷器的稳态特性进行了实验和数值研究,相较于Ng的实验增加了壳程压降对比,实验数据和数值研究结果比较吻合。
目前尚未有对Hampson型换热器稳态特性进行三维数值计算的研究成果,为了更好地了解Hampson换热器内部流动换热特性,本文对其进行三维稳态流动换热数值模拟,并验证该方法的准确性,进而研究肋片形式带来的影响。
1 物理模型及数值模拟方法
1.1 计算模型
1.1.1 物理模型的建立
图1为Hampson型节流制冷机的主要结构,其换热器部分包括壳体(芯轴及外壳)、螺旋肋片管、垫条三部分。在壳程的流动换热过程中,肋片管起到了最主要的强化作用,因此将壳体简化成为绝热壁面,省略垫条结构。由此建立的计算物理模型如图2所示。
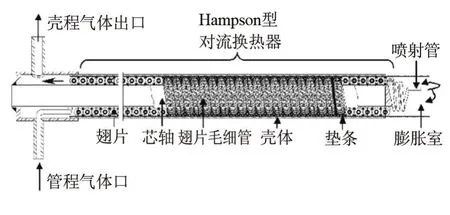
图1 Hampson型节流制冷机主要结构示意图Fig.1 Main structure of Hampson throttling refrigerator

图2 Hampson型换热器简化模型图Fig.2 Simplified model of Hampson heat exchanger
为了研究肋片形式对流动换热的影响,引入了管壳式肋片管换热器中出现频率较高、便于移植的四种肋片形式,其物理模型如图3所示。其中,螺旋形肋片为最常用的肋片形式。

图3 肋片的物理模型图Fig.3 Physical model of fins
1.1.2 网格划分
采用多面体网格划分技术,在保证计算准确性的前提下,缩减单元数目至相同网格参数四面体网格数目的1/3,可大幅提高计算效率。网格示意图如图4所示。

图4 整体网格示意图Fig.4 Overall grid diagram
1.2 基本方程和数值方法
为了解决Standard k-ε在较大逆压力梯度下准确性下降的问题,Shih等[7]于1995年提出Realizable k-ε湍流模型。该模型计算旋转流动、二次流有着更好的效果[8],适用于本文中的计算。相关控制方程及湍流方程如下:

式中:u为流体速度,m·s-1;ρ为流体密度,kg·m-3;μ为动力黏度,m2·s-1;p为压力,Pa;Cp为定压比热容,kJ·kg-1·K-1;t为温度,K;k为湍流脉动动能,m2·s-2;ε为湍流脉动动能耗散率,m-2·s-3;Gk为湍动能的速度梯度项;Gb为湍动能浮力项;YM为总耗散率的湍流脉动膨胀项;Sk为源项。,。
Realizable k-ε模型的经验常数建议使用:σk=1.0,σε=1.9,C2=1.44,C1ε=1.2。
此外,在计算中还采用了尺度化壁面函数、无滑移绝热边界和压力基耦合算法,并考虑了可压缩性影响和黏性热。
1.3 边界条件
本文以文献[2]中的实验数据为基准,给出了5种工况下相应的管、壳程边界条件。其中,管程进口为定压力边界,出口为定质量流边界,参数与文献[2]中一致。壳程采用质量流进口边界,数值与管程相同;压力出口边界由各工况实验验证结果确定。壳体内外壁面、毛细管端面均按无滑移绝热壁面处理,毛细管内、外壁为无滑移耦合壁面。
1.4 模型验证
1.4.1 实验验证
为了确保数学模型的正确性,将计算结果与文献[2]中的实验数据进行了对比验证,结果如表1所列。表中,下标h、c、in及out分别表示管程、壳程、进口及出口。
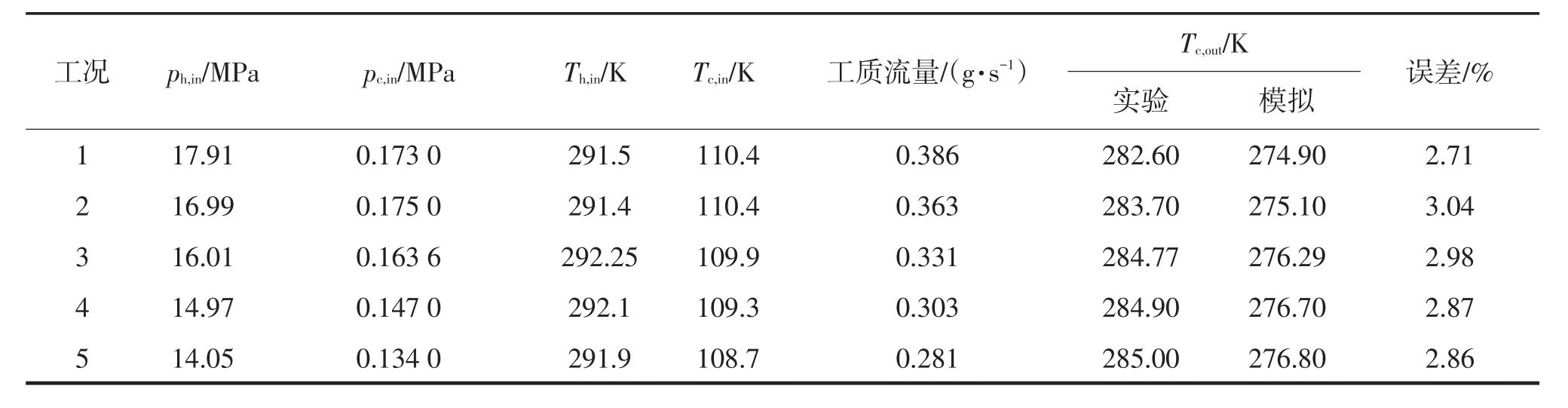
表1 5种工况下相应的壳程边界条件的实验验证结果Tab.1 Experimental verification results of corresponding shell boundary conditions under five working conditions
误差在可接受范围内,模拟结果略低于实验结果,分析是由以下原因造成:
(1)由于实验中物理模型较为复杂,肋片管螺旋共计50圈,为了降低网格划分难度,减少计算量,将连续螺旋肋片简化为了环形肋片,并将肋片高度降低了0.05 mm,减弱了肋片的强化换热效果,但减弱程度十分有限,影响较小;
(2)实验中还在螺旋肋片毛细管间缠绕了两条尼龙细绳作为垫条,以进一步减少流通面积,增大湍动强度,增强换热,为了降低网格量,在数值模拟中对此进行了简化。
从表1可知,当管程进气压力(ph,in)从14 MPa上升到18 MPa时,相应的工质流量从0.281 g·s-1增加到0.386 g·s-1,流量与压力的关系大致成线性变化。
1.4.2 网格无关性验证
当网格量增加至780万时,对数换热温差的变化率小于1%,压降的变化率小于1.2%,因此选择采用此套网格对应的设置来划分后续计算的网格。
2 数值计算
2.1 几何参数
为了研究肋片形式对Hampson型肋片管换热器流动换热性能的影响,建立了多个物理模型,模型之间通用的几何参数如表2所示。
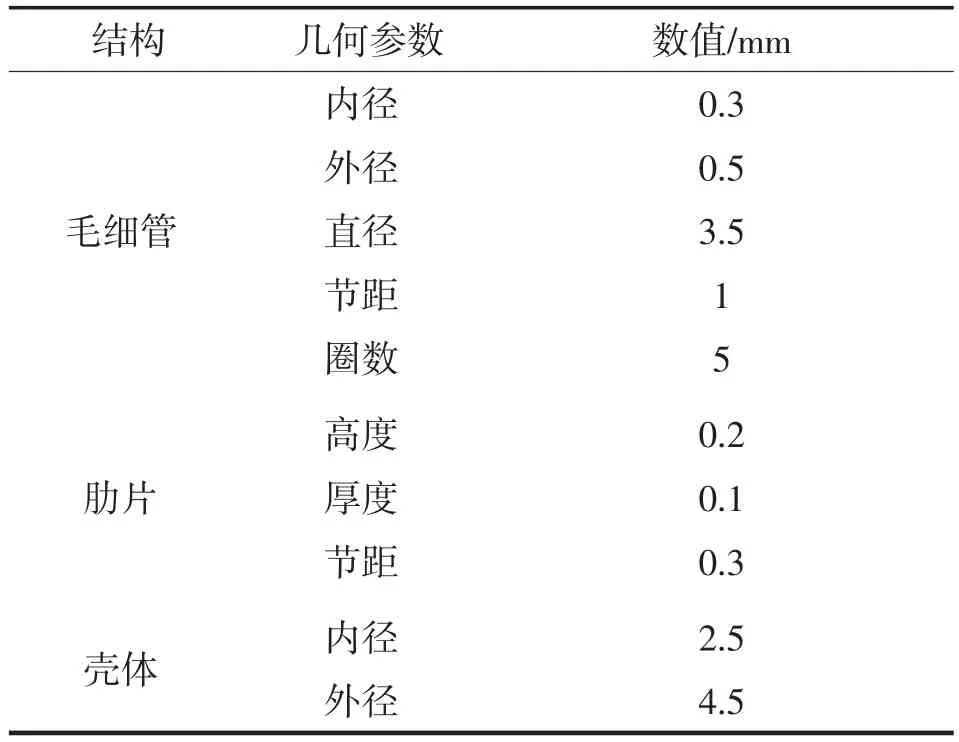
表2 计算模型几何参数Tab.2 Geometric parameters of computation model
在肋片的基本参数不变的基础上,环形肋片与基管表面垂直;锯齿形肋片对螺旋肋片做了剖切,间隔角度为12°,肋片角度为24°;扭曲锯齿肋片将锯齿肋片整体沿螺旋方向倾斜了15°。
2.2 数据处理方法
本文中使用的数据处理方法如下:
有效换热螺旋段光管外表面积:

式中:N为螺旋管的螺旋圈数;DTo为毛细管外径;DTs为毛细管内径。
水力直径:

对数换热温差:
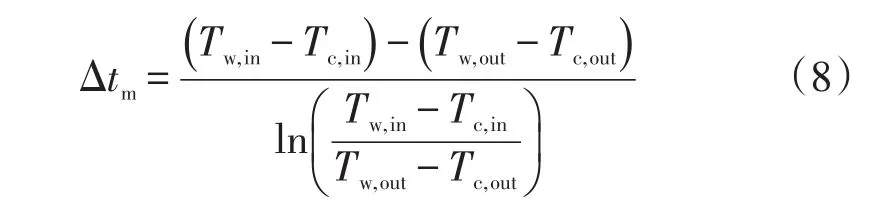
壳程对流换热系数:
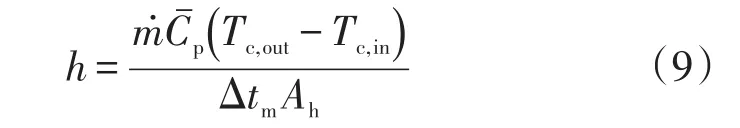
壳程Nu:

壳程Eu:
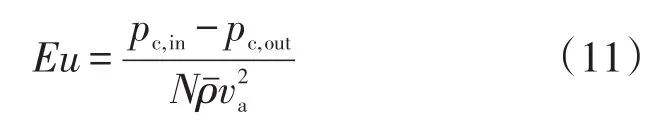
壳程Re:

式中:Δtm为平均对数换热温差;ṁ为工质的质量流量;va为流体平均速度。
3 结果分析与讨论
3.1 壳程流动特性
四种肋片形式壳程轴向流场对比如图5所示。可以看到,环形与螺旋肋片对流动的影响比较类似,肋片上下侧都存在较大的流动死区,整体流动速度较低。锯齿形肋片增大了对壳程流体的扰动,很大程度上提升了近内、外壁面流速,但对于流动死区没有明显的削弱作用。与锯齿形肋片相比,扭曲锯齿肋片由于与基管表面成15°角,增加了对基管上下侧流体的扰动,对近壁面流速的提升和流动死区的减小都有着非常明显的改善效果。

图5 四种形式肋片壳程轴向局部流场对比图Fig.5 Comparison of axial local flow field in shell side of four fin types
通过图6对比不同进气压力下四种肋片形式的壳程Eu可以看到,环形肋片的流动阻力和螺旋形肋片相近,在进口压力相同的情况下,环形肋片的Eu降低了3.53%~3.97%。锯齿肋片和扭曲锯齿肋片Eu则有非常显著的增加,锯齿肋片Eu提升94.82%~95.74%,扭曲锯齿肋片提升119.16%~121.14%。随着进气压力的升高,Eu增加幅度略有降低,这与文献中的研究结果类似。此外,随着进气压力的升高,四种肋片形式的Eu逐渐降低,总体降幅在7.76%~9.02%之间,各形式肋片之间差距不大。这是由于当进气压力上升时,流体流量增大,流速增大,相应的压降也增大。由于Eu与压降成正比关系,而与流速的平方成反比关系,因此随着进气压力的上升,Eu会逐渐减小。
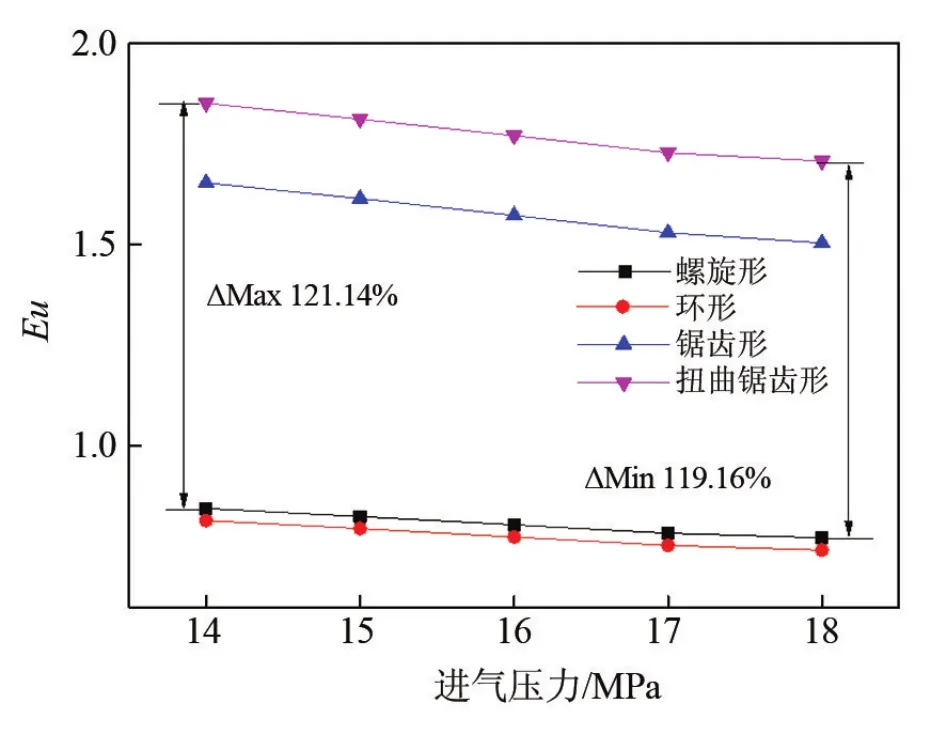
图6 不同进气压力下四种形式肋片壳程Eu对比图Fig.6 Comparison of shell side Eu of four fin forms under different inlet pressure
3.1 壳程换热特性
图7对比了进气压力为18 MPa时,四种形式肋片管外壁面的局部对流换热系数。
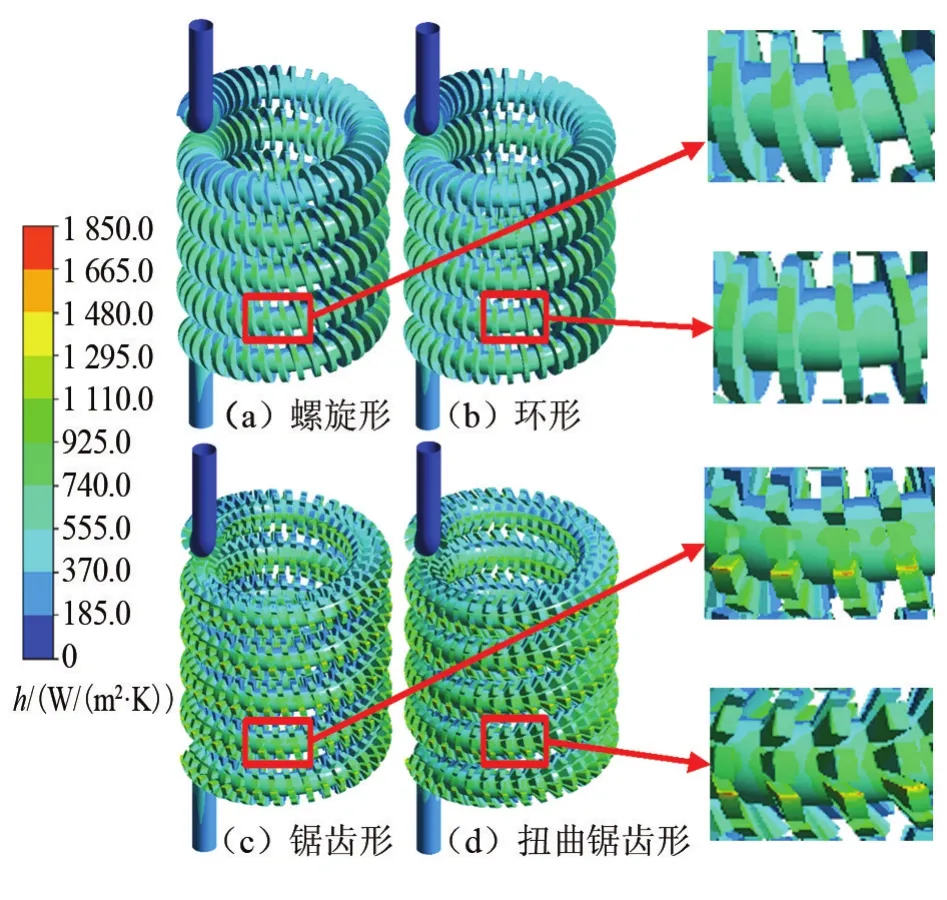
图7 四种形式肋片管外壁面局部对流换热系数分布图(进气压力18 MPa)Fig.7 The distribution of local convective heat transfer coefficient on the outer tube wall of four fin forms(with inlet pressure at 18 MPa)
由图7可以看出,螺旋肋片和环形肋片整体的局部对流换热系数在数值上整体小于锯齿肋片和扭曲锯齿肋片,与流场分析中的结果对应,后两者的壳程流体流速高,流动边界层薄,对流换热更加强烈。此外,螺旋和环形肋片的局部对流换热系数最大位置出现在外侧斜上方肋顶面,而锯齿以及扭曲锯齿肋片则出现在垂直来流的肋片断面外边缘。这是由于螺旋和环形肋片正上部流体流速缓慢,流动边界层厚;肋片侧面流速快,但流动方向与肋片切向平行,流体对肋片的冲击弱,湍动程度低;而在斜上部流体流速较大,对肋片的冲刷能力较强,湍动强烈等因素造成的。锯齿及扭曲锯齿肋片在肋片断面处流体流速高,流动方向垂直肋片断面,流体冲刷断面,湍动强烈,促进了换热。
图8为不同进气压力下四种形式的肋片壳程Nu对比。同压力下,环形肋片对壳程Nu影响不大,仅提高了0.27%~0.80%;锯齿形肋片则可提升29.62%~30.97%;扭曲锯齿形肋片提升38.98%~40.35%,换热效果最佳。此外,随着进气压力的增加,螺旋形肋片Nu增幅为23.96%;环形与扭曲锯齿形肋片分别为23.30%和25.09%;锯齿形肋片增幅最高,为25.25%。这是由于进气压力上升,流体流量增大,流速增大,流体湍动增强,强化了换热,因此Nu随进气压力的上升而增大。
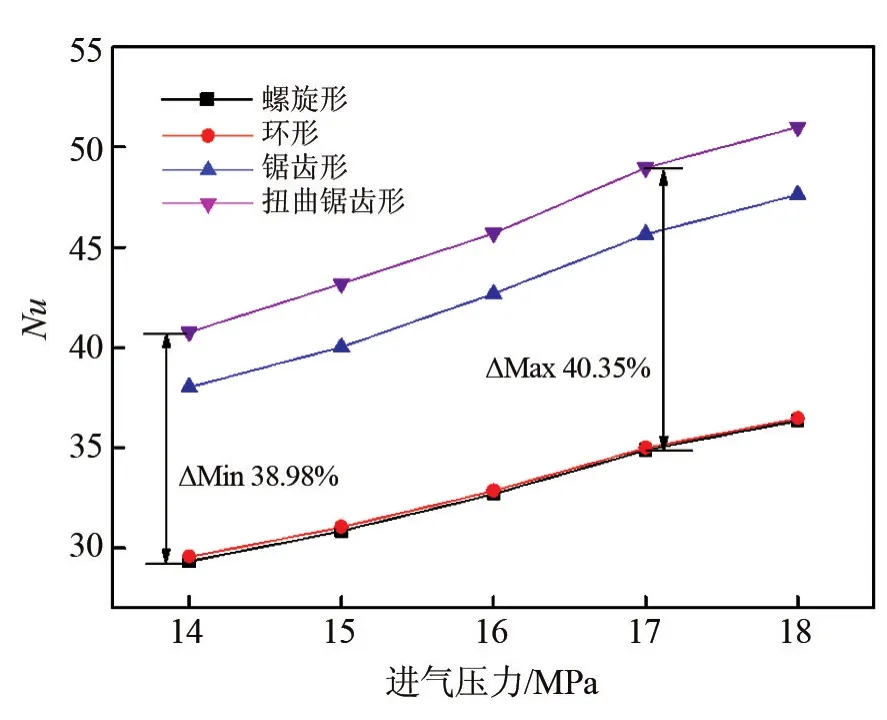
图8 不同进气压力下四种形式肋片壳程Nu对比图Fig.8 Comparison of shell side Nu of four fin forms under different inlet pressure
3.2 综合对比
为了综合衡量三种肋片的综合流动传热效果,以螺旋形肋片作为参照,使用PEC准则数进行对比。计算方法如式(13)所示。
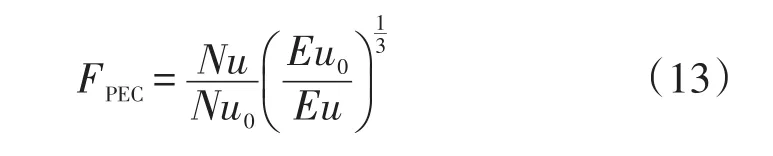
图9为三种形式肋片的PEC准则数。可以发现,相较于螺旋形肋片,三种形式肋片的综合强化换热性能均有提升。环形肋片在降低流阻的同时强化了换热,综合强化换热性能略大于1;锯齿肋片虽然给流动增加了阻力,但可以在很大程度上增强壳程换热性能,因此综合强化性能高于环形肋片;扭曲肋片对换热提升显著,虽然流阻也有明显增加,但综合效果比锯齿肋片有进一步提升。因此,从综合强化换热来看,扭曲锯齿形肋片效果最佳。
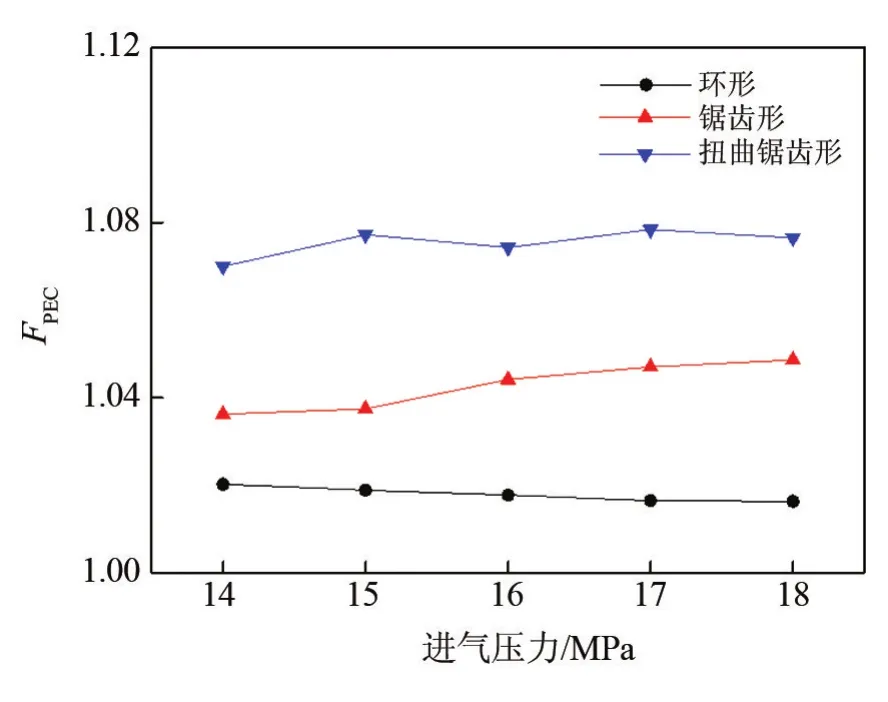
图9 不同进气压力下三种肋片的PEC准则数对比图Fig.9 Comparison of PEC criterion numbers of three fin forms under different inlet pressures
4 结论
通过对多种形式肋片的Hampson型换热器的流动换热数值模拟,对比分析得到了以下结论:
(1)相较于螺旋形肋片,锯齿形肋片能极大地提升近内、外壁面流速,但对于流动死区没有明显的削弱作用。而扭曲锯齿形肋片不仅能显著提高近壁面流速,并且对流动死区也有非常明显的削减作用。
(2)环形肋片会使Eu减小3.53%~3.97%、同时使Nu上升0.27%~0.80%;而锯齿形肋片会使Nu上升29.62%~30.97%,同时使Eu增大94.82%~95.74%。二者PEC准则数均大于1,综合性能较螺旋形肋片有所提升。
(3)扭曲锯齿肋片流动与换热综合优化效果最佳。扭曲锯齿肋片使Eu数上升119.16%~121.14%,同时使Nu上升38.98%~40.35%,PEC准则数为1.070~1.078,综合强化换热效果有较大提高。

