基于AMESim粉碎机液压马达的特性分析
孙伟光 张健 王占军
摘要:针对木材粉碎机启动电流大、工作速度高、停止时候转动惯量大容易损坏电机的问题,提出液压马达解决方案。利用AMESIM软件建立粉碎机液压马达的数学模型,对液压马达的启动、工作、停止过程转动惯量、负载扭矩进行了研究,分析液压马达仿真的结果,提出使用液压马达的注意事项。
关键词:液压马达;AMESim仿真;转动惯量;木材粉碎机;数学模型 文献标识码:A
中图分类号:TH137 文章编号:1009-2374(2015)08- DOI:10.13535/j.cnki.11-4406/n.2015.
随着现在城市规模的越来越大,绿化树木的植物垃圾急剧增多,如集中堆积就会占据宝贵土地资源;如拉到郊区就会增加大量的人力、运输成本。木材粉碎机是专门对植物垃圾进行粉碎处理。但是木材粉碎机电机为工业用电,普通木材粉碎机受电源限制。也有柴油机驱动,扩大了粉碎机的应用场所,但是发动机产生的噪音、污染也不容忽视。
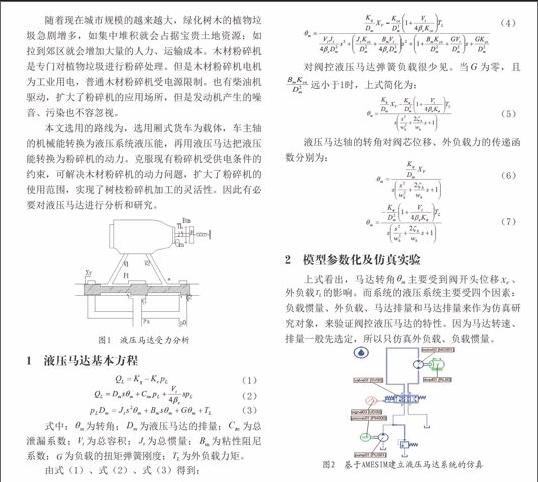
本文选用的路线为,选用厢式货车为载体,车主轴的机械能转换为液压系统液压能,再用液压马达把液压能转换为粉碎机的动力。克服现有粉碎机受供电条件的约束,可解决木材粉碎机的动力问题,扩大了粉碎机的使用范围,实现了树枝粉碎机加工的灵活性。因此有必要对液压马达进行分析和研究。
(3)
式中:为转角;为液压马达的排量;为总泄漏系数;为总容积;为总惯量;为粘性阻尼系数;为负载的扭矩弹簧刚度;为外负载力矩。
由式(1)、式(2)、式(3)得到:
(4)
对阀控液压马达弹簧负载很少见。当为零,且远小于1时,上式简化为:
液压马达轴的转角对阀芯位移、外负载力的传递函数分别为:
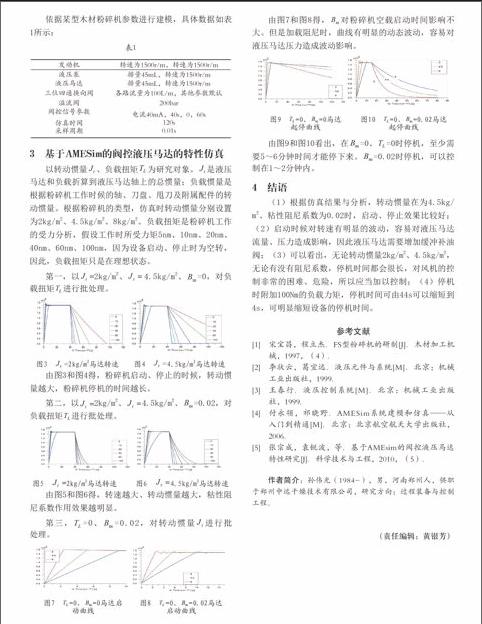
2 模型参数化及仿真实验
上式看出,马达转角主要受到阀开头位移、外负载的影响。而系统的液压系统主要受四个因素:负载惯量、外负载、马达排量和马达排量来作为仿真研究对象,来验证阀控液压马达的特性。因为马达转速、排量一般先选定,所以只仿真外负载、负载惯量。
依据某型木材粉碎机参数进行建模,具体数据如表1所示:
3 基于AMEsim的阀控液压马达的特性仿真
以转动惯量、负载扭矩为研究对象。是液压马达和负载折算到液压马达轴上的总惯量;负载惯量是根据粉碎机工作时候的轴、刀盘、甩刀及附属配件的转动惯量。根据粉碎机的类型,仿真时转动惯量分别设置为2kg/m2、4.5kg/m2、8kg/m2。负载扭矩是粉碎机工作的受力分析,假设工作时所受力矩5nm、10nm、20nm、40nm、60nm、100nm,因为设备启动、停止时为空转,因此,负载扭矩只是在理想状态。
第一,以2kg/m2、4.5kg/m2、=0,对负载扭矩进行批处理。
由图3和图4得,粉碎机启动、停止的时候,转动惯量越大,粉碎机停机的时间越长。
第二,以2kg/m2、4.5kg/m2、=0.02,对负载扭矩进行批处理。
由图5和图6得,转速越大、转动惯量越大,粘性阻尼系数作用效果越明显。
第三,=0、=0、0.02,对转动惯量进行批处理。
由图7和图8得,对粉碎机空载启动时间影响不大。但是加载阻尼时,曲线有明显的动态波动,容易对液压马达压力造成波动影响。
由图9和图10看出,在=0、=0时停机,至少需要5~6分钟时间才能停下来。=0.02时停机,可以控制在1~2分钟内。
4 结语
(1)根据仿真结果与分析,转动惯量在为4.5kg/m2、粘性阻尼系数为0.02时,启动、停止效果比较好;(2)启动时候对转速有明显的波动,容易对液压马达流量、压力造成影响,因此液压马达需要增加缓冲补油阀;(3)可以看出,无论转动惯量2kg/m2、4.5kg/m2,无论有没有阻尼系数,停机时间都会很长,对风机的控制非常的困难、危险,所以应当加以控制;(4)停机时附加100Nm的负载力矩,停机时间可由44s可以缩短到4s,可明显缩短设备的停机时间。
参考文献
[1] 宋宝昌,程立杰.FS型粉碎机的研制[J].木材加工机械,1997,(4).
[2] 李状云,葛宜远.液压元件与系统[M].北京:机械工业出版社,1999.
[3] 王春行.液压控制系统[M].北京:机械工业出版社,1999.
[4] 付永领,祁晓野.AMESim系统建模和仿真——从入门到精通[M].北京:北京航空航天大学出版社,2006.
[5] 张宗成,袁锐波,等.基于AMEsim的阀控液压马达特性研究[J].科学技术与工程,2010,(5).
作者简介:孙伟光(1984-),男,河南郑州人,供职于郑州中远干燥技术有限公司,研究方向:过程装备与控制
工程。
(责任编辑:黄银芳)

