构建非结构网格高精度有限体积方法的新途径

任玉新，王乾，潘建华，章雨思，黄乾旻

清华大学 航天航空学院，北京 100084

湍流与转捩(尤其是高超湍流与转捩)、湍流分离流、激波/边界层干扰、气动声学、湍流燃烧等问题是飞行器设计中的关键科学问题。这类问题具有多尺度、非线性、非定常、存在流场间断等特点，对高可信度数值模拟提出了很高的要求。以湍流模拟为例，以目前计算机的能力已可以很好地满足RANS(Reynolds-Averaged Navier-Stokes)模拟的需求，也可以开展部分RANS/LES(Large Eddy Simulation)混合模拟的工作；但还远远不能满足LES和DNS(Direct Numerical Simulation) 的需求。未来先进飞行器将具有复杂构型、高机动、先进动力系统、多变飞行环境等特征，对数值模拟的要求更高，RANS模拟在很多情况下不能满足需求，预计LES将成为研究复杂湍流的主要手段。此时，提高计算效率、降低计算成本将成为计算流体力学(Computational Fluid Dynamics，CFD)发展的驱动力之一[1]。

计算成本包括时间成本和费用成本(二者相关，但其关系依赖于计算机架构及模拟策略)。其中时间成本可通过发展高速超算设备控制，而费用成本则与总计算量有关。即使未来计算机的发展使高雷诺数LES和DNS成为可能，但按现在超算收费标准，其费用仍然难以承受。发展高精度格式的学术意义在于有可能实现在一定计算误差的前提下使计算量更小、计算时间更短；或在同样的计算机机时消耗下得到的数值解精度更高。因此，发展高精度格式是提高计算效率、降低计算费用成本的有效途径之一。为进一步阐明这一判断，定义数值方法的计算效率为

(1)

式中：ε为在某个特定网格下数值解与真值的误差；τ为开展相应计算所用时间；h为相应网格的特征尺度。显然，计算效率是依赖具体问题和计算网格的。对于k阶精度格式，当网格尺度变为原来的1/2，则误差变为原来的1/2k。同时，网格尺度变为原来的1/2后，三维问题网格数增加到原来的8倍。考虑显式格式时间步长也要减半，其总计算量至少增加到原来的16即24倍。对于隐式格式，网格增多后，其迭代收敛速度通常会变慢，计算量至少增加到原来的16倍也是比较合理的估计。因此有ε(h/2)=ε(h)/2k，τ(h/2)=24τ(h)，即η(h/2)=2k-4η(h)。

显然，对小于四阶精度的格式，其计算效率随网格加密而下降。例如，二阶格式当网格间距变为原来的1/2时，计算效率变为原来的1/4。当进行RANS或无黏流计算时，对网格数的要求相对较低，二阶格式简单、易行，可能是较好的选择；当开展LES或者DNS计算时，二阶格式的计算效率会显著下降，发展高精度格式的必要性得到凸显。

由于非结构网格生成具有灵活、高效、自动化程度高的优点，基于非结构网格的数值方法在CFD软件中占据主流[2]。可以预见，非结构网格高精度数值方法也将是新一代CFD软件的主导算法[2]。因此，非结构网格高精度数值方法最近得到了高度重视，已经发展出很多有效算法。其中，高精度有限体积方法是最早得到发展的方法，为二阶精度有限体积方法的直接发展。为实现高阶精度，必须在每个控制体(单元)内部获得物理量的高阶分布,这个分布通常用多项式表示。由于有限体积方法直接求解的是守恒变量在单元上的平均值,为确定多项式的待定系数，只依靠本单元的信息是不够的，必须使用本单元及其足够数量相邻单元的平均值反推多项式的待定系数,这个过程称为重构(Reconstruction)[3]。参与重构的所有单元构成的集合称为重构的模板(Stencil)。即使获得了高阶的重构多项式，通常也不能直接用于计算包含激波间断的可压缩流动，因为会在间断附近产生非物理的数值振荡。为抑制在间断附近的振荡，必须采用合理的限制措施。限制过程是某种非线性滤波运算，其中的非线性平均算子称为限制器(Limiter)[4]。重构和限制过程是高精度有限体积方法的关键难点问题。

在20世纪90年代，Barth和Frederickson[5]提出了基于最小二乘法数据重构的k-exact高精度有限体积方法。此方法的优点是可以较简单、系统地确定重构模板，每个单元只需进行一次重构；其缺点是没有很好地解决激波捕捉的梯度限制问题，对激波的计算能力较差。通常采用的Barth[6]及Venkatakrishnan[7]限制器耗散很大，对激波和光滑流动结构的分辨能力都较差。

WENO(Weighted Essentially Non-Oscillatory)方法[8-9]是构造非结构网格高精度有限体积格式的有效途径。WENO方法通过几个候选重构多项式的非线性加权平均得到最终的重构多项式。此方法把重构和限制过程有机地结合起来，因此具有很好的激波捕捉能力，但其代价是需要确定多个重构模板、进行多次重构，因而算法复杂、计算量很大。

在高阶重构过程中需要很大的重构模板，是高精度有限体积方法始终无法回避的问题。造成重构模板巨大的本质原因是对于某一个单元的多项式重构，其重构模板中的每一个单元只有一个可以利用的自由度，即物理量的单元平均值。如在k-exact重构中，一个模板单元只能提供一个线性方程。为使得k-exact重构稳定，一般模板中单元数目取值应显著大于待定系数数目[10]，并使用最小二乘方法求解重构方程组。因此随着重构多项式阶次的提高，待定系数数目迅速增大，重构模板也相应地变得巨大。重构模板巨大会导致一系列影响计算效率和鲁棒性的问题，如要利用较远的模板单元而使计算缓存利用率低、分区交界面上要传递的数据多而使并行计算效率降低、物理边界处模板偏心化而加大重构奇异性等。另外，对于程序设计，重构模板巨大的一个弊端是其不确定性。在搜索模板时，常常是逐层向外扩展，但经常出现某一层模板单元太多的情况，全部采用则计算量和存储量增加过多，只用部分单元的话又需要设计取舍的准则，这给程序设计带来了很大不便。

为克服高阶有限体积格式的这些缺点，最近一些新型的、适用于非结构网格的高精度算法得到了高度重视。它们和有限体积方法的最著区别是在确定近似解的分片光滑多项式过程中，主要不是从外部(相邻单元)获取信息，而是试图从单元内部得到更多的额外信息，从而保证格式模板的紧凑。为阐述方便，统称这些方法为非结构网格上的亚网格自由度高阶格式。其代表性的工作有间断迦辽金有限元方法(Discontinuous Galerkin method，DG)[11-13]、谱体积方法(Spectral Volume method，SV)[14]、谱差分方法(Spectral Difference method，SD)[15]。最近，Huynh[16]和王志坚[17]等提出了FR(Flux Reconstruction)/CPR(Correction Procedure via Reconstruction)方法，可以把SD、DG等方法归纳到一个统一框架中。此外，亚网格自由度高阶算法和有限体积(Finite Volume，FV)方法重构过程的结合也得到了重视，发展了PNPM方法[18-19]、rDG(reconstructed DG)方法[20-21]、DG/FV混合算法[22]、PNPM-CPR 方法[23]、multi-moment方法[24]等。

亚网格自由度高阶算法的共同优点是计算模板紧凑。这个特点使得这些方法在大规模计算中具有内存寻址消耗小、对计算机缓存的利用率高、并行计算的效率较高、与一些新HPC(High Performance Computing)体系结构(如基于GPU(Graphics Processing Unit)的并行计算)的相容性较好等优点，显著优于传统高阶有限体积格式。此外，这些方法对光滑流场的计算精度和分辨率很高。然而，这些方法还存在一些尚未完全解决的问题，主要有计算包含激波间断的流场时缺乏高效、保持精度的限制器或非线性人工黏性方案；计算含强激波、强膨胀波和几何突变的流场时鲁棒性较差；隐式格式规模很大，需要尽量精确地计算雅可比矩阵并加以存储，对存储量有很高要求，目前迫切需要发展高效、低存储的隐式时间积分技术；高阶格式需要基于高阶网格，目前的网格生成软件还不能完全满足需求。由于这些原因，基于这些方法的商业化CFD软件发展还相当滞后。

相反，有限体积方法发展相对成熟，在保精度限制器、高效隐式积分等方面已有较好的解决方案，对计算量和存储量的需求也相对较低。如果能够解决重构模板巨大这一瓶颈问题，应该具有很好的发展前景。发展基于紧致模板的重构方法是近期工作的出发点。

所谓紧致模板，即只包含当前单元及其有公共面(三维)或公共边(二维)的单元的模板。通过仔细研究有限体积方法的重构过程发现，由于在重构模板中的每一个单元上只能提供一个平均值信息，要获得高阶重构多项式，必然要使用很大的模板或者提供额外的信息。为解决这一难题，提出操作紧致性这一重要概念。所谓操作紧致性，即不要求实际上采用的模板是紧致的，只要求在数值求解过程中所有的数据结构和计算操作都只用到紧致模板中的信息。操作紧致性的概念为实现基于紧致模板的重构提供了广阔的空间。基于这一概念，提出了几种紧致重构方法。这些方法可以分为两类，即隐式重构和显式重构。

在隐式重构方面提出了紧致最小二乘重构[25-26]和变分重构[27]方法。目前广泛使用的高精度重构方法对于每一个模板单元都只利用了一个信息，即物理量的单元平均值。这样一来要确定单元上的重构多项式系数，就需要个数不少于重构多项式系数的模板单元，这就是现有重构方案模板巨大的根本原因。为发展紧致高精度重构，必须突破每个模板单元只贡献一个信息的思路，采取“挖掘更多信息，使用更小模板”的策略。为在只包括面相邻单元的模板上实施高阶重构，不仅要利用面相邻单元的物理量平均值，还要利用面相邻单元物理量的导数。由于面相邻单元物理量的导数也是待定的，所以和结构网格上的紧致差分方法类似，这类重构过程是隐式的。隐式重构面临的主要困难是需要求解大型稀疏矩阵对应的线性方程组，因而计算量很大。通过两个手段可以显著提高计算效率：其一是通过迭代法求解重构过程；其二是与隐式时间推进相结合，将重构的迭代和隐式格式迭代求解的过程同步进行。这些方法可使基于隐式重构的有限体积格式计算效率与隐式k-exact格式相当。

在显式重构方面提出了多步重构方法[28]。多步重构通过不断扩展原始重构关系，每一步一般可提高一阶精度，从而逐步达到高阶精度。这本质上是一个逐步扩大模板的过程，但在操作层面只需处理紧致模板的信息。显式重构的优点是与显式和隐式时间推进方法相结合都可以达到较高计算效率；而隐式重构只有采用隐式时间积分时才可能有较高计算效率。因此，显式重构比隐式重构在时间推进方面有更大的灵活性。

除重构过程外，高精度有限体积方法还必须解决边界条件、激波捕捉、时间推进、高阶网格计算等一系列问题。本文对此也将做简要介绍。

本文首先概要介绍有限体积方法的基本理论，重点对常见的k-exact重构进行介绍，分析大模板问题的来源；然后详细介绍3种紧致重构方法，即紧致最小二乘重构、变分重构和多步重构；接着进一步介绍紧致重构有限体积方法的实施、效率提升、边界处理、激波捕捉、高阶网格、时间推进、方法性能等问题，并简述近期的发展；最后给出结论。

1 有限体积方法基本原理

原则上，有限体积方法可求解双曲型、抛物型、椭圆型及其他偏微分方程对应的积分型方程。其中最为重要的应用是求解流体力学中的守恒律方程。常见的Euler方程和Navier-Stokes方程都可以写成守恒律。以二维三角形网格上求解守恒律的有限体积格式为例做进一步介绍。一般的二维守恒型方程组可以写为

(2)

式中：U为守恒变量，对于二维Euler方程和Navier-Stokes方程而言，为有4个分量的列向量；F和G为通量函数；t、x和y分别为时间变量及空间的两个笛卡尔坐标。一般而言，一阶守恒律中F和G为U的函数(如Euler方程)；二阶守恒律中F和G为U及其梯度的函数(如Navier-Stokes方程)。在图1所示控制体Ωi上对式(2)积分，并利用Gauss公式得到

(3)

图1 有限体积方法的控制体Fig.1 Control volume of finite volume method

外法向量；S为控制体界面面积。

式(3)即为有限体积方法求解的积分型方程。事实上，式(3)不一定依赖于式(2)，常常可以从基本守恒定律直接导出。

直接对式(3)进行空间离散的有限体积方法称为半离散型有限体积方法。另一种方案即所谓全离散有限体积方法，其基本方程可以通过对式(3) 在一个时间步内积分得到，即

(4)

式中：n为数值计算的时间步；Δt为时间步长；tn为n时间步对应的时刻。

无论是全离散还是半离散有限体积方法，其因变量均为物理量在控制体上的平均值。而式(3)、式(4)的空间项涉及物理量在界面上的分布及其演化。因此，为用数值方法求解式(3)、式(4)，必须引入各种近似。这些近似构成了有限体积方法的基本要素。为更好地解释这些要素，将有限体积方法抽象地写为如式(5)和式(6)的形式：

全离散有限体积格式为

(5)

半离散有限体积格式为

(6)

式中：MS为控制体边数，对于图1所示三角形控制体，MS=3；RΩ、EΔt(或为E0)分别为重构和演化积分算子；Im为沿控制体第m个边的数值通量积分算子；Si为重构模板，其具体含义将在1.1节中介绍。Im的构造比较直接，其意义为

(7)

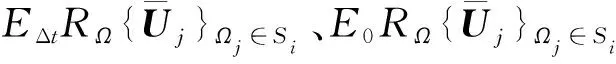
1.1 重 构

有限体积方法能够得到的是物理量在各个控制体上的平均值，而有限体积方法的核心要素——数值通量的计算涉及物理量在界面上的分布及其演化。为计算数值通量，需要利用物理量在各个控制体上的平均值构造出物理量的分布。这一过程称为重构，式(5)、式(6)中的RΩ称为重构算子。重构函数是分别定义在各个控制体上的分片光滑函数，一般为多项式。

在有限体积方法的实施中，对守恒变量U的分量u逐一进行重构。控制体Ωi上，守恒变量的重构函数记为Ui(x,t)，对于二维情形，x=xi+yj。只考虑Ui(x,t)的一个分量ui(x,t)的重构问题。由于整个重构过程是在同一个时刻进行的，因此省略时间变量t，将重构多项式记为ui(x)。一般而言，基于k次多项式重构的有限体积方法，其空间精度为k+1阶。其中零阶重构最为简单，假定每个控制体内ui(x)为常数(零次多项式)，即为单元平均值。Barth和Frederickson[5]提出的k-exact重构方法可以进行任意次数的多项式重构，从而可以构造任意阶空间精度的有限体积方法；他们还提出了对重构过程的3个基本要求：

2)k-exact性质，即k次多项式重构可以准确复现次数不高于k的多项式精确解。

3) 紧凑性。有限体积方法只能提供每个控制体物理量的平均值，而当k>0时，每个单元重构多项式的待定系数个数大于1。因此，在Ωi单元进行重构时，必须利用其相邻的多个控制体上平均值的信息。参与Ωi单元重构的单元集合称为Ωi单元的重构模板。所谓紧凑性，即要求重构模板中的单元应优先选取邻近Ωi的控制体。

k-exact重构的主要困难在于随重构多项式次数的提高，重构模板中所需控制体的个数显著增加，这就是所谓大模板问题。大模板问题增加了编程复杂度，降低了并行计算的效率，且难以以高精度实施边界条件。

为更清楚地说明大模板问题的来源，简要回顾k-exact重构。设当前时刻计算域上所有单元的平均值已知，重构算法需要给出u在计算域上的一个分片连续的k次多项式分布，即在任意一个单元Ωi上，用k次多项式式(8)逼近u在单元i中的分布：

(8)

(9)

式中：p和q均为基函数的次数；dΩ为体积微元；xi和yi为控制体的形心坐标；Δxi和Δyi为用来对基函数进行无量纲化的特征尺度，可以有多种选择，这里采用Luo等[29]的方案：

(10)

式中：xmax、ymax和xmin、ymin分别单元i的x、y坐标最大值和最小值。基函数的无量纲化能够克服重构矩阵条件数随网格加密而增大的问题[9]。用k=2的重构多项式举例说明指标l与p、q之间的关系：

(11)

(12)

给定阶次k时，重构多项式可用式(8)～式(10) 表示。重构基于事先选定的重构模板，例图2是在二维三角形单元上进行k=3的三次多项式重构时，Ωi单元的一种可能的重构模板，记为Si。一般来讲，模板中单元的个数ni应满足ni≥Nc(k)。

图2 二维三角形单元的三次k-exact重构模板示意图Fig.2 Schematic diagram of third order k-exact reconstruction on triangular cells in 2D

k-exact重构的基本原理是利用k-exact性质导出重构关系。对于充分光滑的函数u(x)(精确解)，在Ωi的不小于重构模板Si的邻域内，总是可以找到一个k次多项式p(x)，使其逼近精确解u(x) 到k+1阶精度，即

p(x)=u(x)+O(hk+1)

(13)

式中：O(hk+1)为无穷小量。

(14)

与式(14)相类比，k-exact重构的重构关系可以取

(15)

将式(8)代入式(15)，得

(16)

(17)

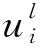
在实际计算中，由于重构多项式采用式(9)的零均值基，当前单元的重构关系即守恒条件式(12) 是自动满足的，因此不能再作为一个重构关系。所以重构关系式(16)可以进一步明确为

(18)

根据对k-exact重构的介绍和分析，可以进一步总结如下：

1) 重构操作是针对充分光滑函数进行的，这是式(13)成立的前提，在这一前提下才能估计重构精度。所述紧致重构也是针对充分光滑函数的。由于可压缩流动可能存在流场间断，在有限体积方法中采用除零阶重构以外的较高精度重构时，数值解会在间断附近产生非物理振荡。由于间断总是局限在某些线或面上，流场大部分区域还是可以采用对光滑函数的重构算法。在间断附近，需要引入某种限制器对重构多项式进行局部修正。Van Leer的MUSCL(Monotonic Upwind centered Scheme for Conservation Laws)格式[4]是较早期的限制器构造方案。限制器的构造还可以基于TVD(Total Variation Diminishing)条件[30]、极大值原理(如Barth限制器)[6]或者TVB(Total Variation Bounded)条件(如著名的ENO(Essentially Non-Oscillatory)和WENO格式[31]等。

2) 在求解方程组式(18)时，要求线性方程组系数矩阵非奇异，或在最小二乘意义下非奇异；而且矩阵条件数对重构精度有直接影响。为满足这些要求，在非结构网格上一般采用最小二乘法求解式(18)。经验表明，比较合适的模板中单元数量为待定系数数目的1.5～2.0倍。这就是k-exact重构方法大模板问题的由来。按照这个要求，模板中单元个数随重构多项式次数提高迅速增长。对于三维的三次(k=3)多项式重构，有19个待定系数，需要约30个模板单元，而四次(k=4)多项式重构则需要约50个模板单元。模板巨大会造成一系列的问题:模板单元和中心单元的编号差距大，造成CPU缓存利用率低；并行计算时虚拟网格量大，进程之间需要传递的数据量大，通信时间长，降低并行效率；在边界处，由于需要较多的邻单元，只能向计算域内部扩展模板，造成模板的偏心化，加大重构的奇异性。因此，模板巨大会降低格式的效率和鲁棒性，已成为高精度有限体积方法发展的瓶颈问题。在1.2节将会给出解决这一问题的几种有效方案。

1.2 演 化

双曲型守恒律(如Euler方程)的数值通量或Navier-Stokes方程的无黏部分数值通量计算中，演化过程的研究是计算流体力学发展过程中非常重要的研究内容。著名的Godunov格式[32]是早期的代表性工作。在采用零阶重构的情况下，Godunov格式的演化过程通过求解黎曼问题实现。黎曼问题为双曲型守恒律在分段常数初始条件下的初值问题，对于一维Euler方程存在解析解。由于精确求解黎曼问题计算量较大，还发展了多种黎曼问题的近似解法，代表性的有Roe[33]、Osher[34]和Toro[35]等的近似黎曼求解器,这些黎曼求解器可以通过维数分裂技术推广到多维情况。

对于全离散的有限体积格式，由于要计算数值通量在一个时间步内的演化，其演化过程依赖于重构运算。例如，Godunov格式由于其中的黎曼求解器只能处理分段常数的初值，即只能作用于零阶重构，因而格式只有一阶精度。如果要达到二阶精度，则需求解分段线性函数初值的黎曼问题，称为广义黎曼问题。广义黎曼问题比常规黎曼问题更为复杂，一般没有解析解。Matania和Joseph[36]研究了广义黎曼问题的求解，使得全离散有限体积格式达到了二阶精度。近年来，Toro和Titarev[37]研究了对应更高阶重构的线性化广义黎曼问题或导数黎曼问题，发展了更高阶精度的全离散有限体积格式——ADER格式。徐昆[38]提出的气体动理学格式采用全离散有限体积方法；其演化过程基于简化的玻尔兹曼方程，且可以和任意重构算法相结合。李杰权和杜知方[39]发展的二步四阶格式也可以用于全离散有限体积方法。

半离散有限体积格式由于只需计算数值通量的无穷小时间演化，其演化算子和重构算子是解耦的，因此Godunov[32]、Roe[33]的黎曼求解器均可以和任意重构算法结合，构造出任意空间精度的有限体积格式，而无需求解广义黎曼问题。Van Leer[4]首先认识到半离散有限体积格式的这一特性，从而把Godunov格式推广到高阶精度。

可以证明，基于黎曼求解器的Godunov类格式是一类迎风型格式。对于半离散的有限体积格式，除Godunov类格式外还发展了其他多种迎风型演化算法，如矢通量分裂(Flux Vector Splitting，FVS)格式[40]、AUSM(Advection Upstream Splitting Method)格式[41]等。此外，中心型演化算法也得到了发展。最简单的中心型演化算法是直接对数值求积点两侧物理量取算术平均，但这种方法一般不稳定；Jameson[42]通过添加混合二阶和四阶人工黏性项得到了稳定的有限体积格式；Kurganov和Tadmor[43]通过在控制体界面附近构造辅助控制体、在辅助控制体上求解原方程的方法构造演化算子，也得到了稳定的有限体积格式。

1.3 投影及时间推进

通过重构及演化过程得到了控制体界面处逐点的数值通量。显然，数值通量的计算基于重构函数空间，而有限体积方法的因变量是物理量的单元平均值。从重构函数空间转换到单元平均值的过程称为投影，其操作为如式(7)所示的通量积分过程。对于全离散有限体积方法，通过投影过程可直接得到下一时间步物理量的单元平均值。而对于半离散有限体积方法，投影过程的结果是关于单元平均值时间导数的常微分方程组。为计算下一时间步物理量的单元平均值，还需确定具体的时间推进格式。一般来说，所有求解常微分方程组的数值方法都可作为时间推进格式，如各种Runge-Kutta方法、多步方法及隐式方法等。应该指出，有限体积方法的因变量是物理量的单元平均值，但其最终数值解应视为经重构过程得到的物理量在控制体内部的分布函数；这一点对于正确理解高精度有限体积方法尤为重要。

2 紧致重构

以半离散有限体积方法为例，介绍最近发展的非结构网格高精度有限体积方法的紧致重构算法。重构问题的基本解法在第1节已做介绍。为在紧致模板(即图1所示模板)上实现任意高阶重构，必须有效利用重构过程的信息。对于高阶重构，重构多项式中待定系数的数量很大，但已知信息仅为单元均值，从而造成了所谓大模板问题。操作紧致性是为解决这个问题提出的新思路。从数值计算角度看，操作紧致性对于数据结构设定、程序设计、并行计算而言是和实际模板是紧致的情况完全一样的。事实上，绝对紧致的格式是不存在的。例如DG等方法即使在一个时间步内只用到紧致模板的信息，但还会隐含地用到更早的时间步内、更大范围内网格上的信息。紧致重构方法在一个时间步内就会隐含地用到紧致模板以外的信息，但所有操作都是局部的，只用到紧致模板内的信息。操作紧致性这一概念创新极大扩展了构造重构算法的多样性，使发展高阶紧致重构成为可能。同时，也使高精度紧致有限体积方法可以采用二阶格式的数据结构、计算操作和存储策略，实现高精度计算，从而有效解决了高阶有限体积方法模板过大这一瓶颈问题。下文将逐一介绍提出的紧致重构方法，简单起见，只讨论一维或二维紧致重构。重构均基于紧致模板，即图1中的单元Ωi及其面相邻单元Ωj1、Ωj2、Ωj3。当Ωj单元与Ωi相邻时，则必为Ωj1、Ωj2、Ωj3之一。

2.1 紧致最小二乘重构

在k-exact重构中采用的重构关系如式(18)所示，即

(19)

此时，每个模板中的单元只能提供一个关系，从而造成了所谓大模板问题。注意到由重构的守恒性，式(19)也可以写为

∀Ωj∈Si,j≠i

(20)

即要求ui(x)在Ωj上的平均值与uj(x)在Ωj上的平均值相同。按照“挖掘更多信息，使用更小模板”的思路，对式(20)进行扩展，即不仅要求重构多项式本身满足式(20)，同时要求其各阶导数也满足类似关系，称为导数守恒关系，从而有[25-26]

∀Ωj∈Si,j≠i, 0≤m+n≤M≤k

(21)

式中：M为导数守恒关系中最高阶导数的阶数。取不同的m和n时，式(21)各方程的量纲不同，为此对这些方程进行无量纲化，引入权函数wi,m+n=(whi)m+n，其中w为自由参数，用于控制各个阶次的导数的守恒方程的权重；hi为单元特征长度尺度，一般取为控制体外接圆半径。合理地调节w可以改善格式精度和计算效率，具体可见文献[44]。考虑权函数后的导数守恒关系为

(22)

导数守恒关系中导数阶数为0时，式(21)退化为式(20)。因此，导数守恒关系包含了比常规k-exact重构更多的条件，从而可以缩小重构模板。

将重构多项式式(8)代入式(22)，得到线性方程组：

(23)

(24)

式中：矩阵和向量的定义为

(25)

当将j取遍重构模板中的面相邻单元{j1,j2,j3}并对其对应的线性方程组式(24)进行组装，得到单元i的重构线性方程组：

(26)

式中：

(27)

在二维情况下，一般取导数守恒方程的最高阶次M=k-1。这样一来，重构线性方程组式(26) 的方程个数为3[Nc(k-1)+1]，未知量个数为Nc(k)，可以推导出3[Nc(k-1)+1]-Nc(k)=k2-k+1>0，即方程个数总是大于未知数的个数，二者的数量对比见表1。所以重构线性方程组式(26)是超定的。

表1 2～4阶紧致重构线性方程组的方程和未知量个数

用最小二乘法求解超定线性方程组式(26)，因此这种重构方法称为紧致最小二乘(Compact Least Squares，CLS)重构方法。在一维情况下，全场单元的法方程组成一个块三对角方程组，可以用直接法快速求解；但在多维情况下，非结构网格单元编号是不连续的，中心单元和面相邻单元的编号可能相差很大，因此全场单元的法方程组成一个大型稀疏线性方程组。全场的法方程联立组成一个大型稀疏线性方程组，所以每个单元实际依赖的模板都是全场单元的集合。如用直接法求解，那么求解过程无论如何都不能做到紧致。因此，感兴趣的是能够保持重构方程组求解过程紧致性的迭代方法。如第2节第1段所述，紧致是指求解过程的操作紧致性，即在求解过程的任何一个步骤只需使用面相邻模板单元的信息。程序实施时只需定义基于紧致模板的数据结构，操作上紧致这一性质已足以克服重构模板巨大造成的缓存命中率低及并行计算时进程间的数据交换量大等问题。

采用奇异值分解(Singular Value Decomposition，SVD)方法计算式(26)的最小二乘解，并采用Block Gauss-Seidel方法逐个单元进行迭代求解以保持求解过程的操作紧致性。式(26)的Block Gauss-Seidel迭代公式为

(28)

2.2 变分重构

变分重构[26]是一类模板紧致的高精度重构方法的总称。这类重构方法的原理是定义一个泛函，需要确定的重构关系恰好使泛函取极小值。要求泛函重构基于紧致模板，且具有k-exact性质。为满足这个要求，可以在任意两个控制体的交界面上定义界面跳跃积分(Interfacial Jump Integration，IJI)。即对于一个单元交界面f，令其左、右两侧的单元编号分别是L、R，那么界面f上的IJI定义是

(29)

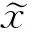
(30)

式中：Nf为计算域上的单元交界面的总数。事实上，当所有控制体的平均值均由同一个次数不高于k的多项式计算，且每个单元的重构多项式均取为这个多项式时，I取其极小值0。因此，这个泛函具有k-exact性质，可以保证重构的精度。

一般情况下，变分重构用来求解重构多项式待定系数的基本关系式是令泛函I取极小值导出的：

(31)

式中:N为控制体总数。

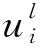
l=1,2,…,Nc(k);i=1,2,…,N

(32)

式中：dij为界面两侧单元形心之间的距离。

式(32)的矩阵形式为

(33)

式中：

(34)

可用精度足够高的高斯数值积分精确地计算重构矩阵表达式中的面积分。

组装所有单元的重构线性方程组式(33)，得到以全场单元的重构多项式待定系数为未知数的大型稀疏线性方程组：

Au=b

(35)

式中：

(36)

可以证明矩阵A具有如下性质：①A是对称的；②A是正定的；③ 2D-A是对称正定的。根据性质 ① 和性质 ②，矩阵A是对称正定的，那么矩阵A一定是可逆的，变分重构的线性方程组式(35) 有唯一解。重构矩阵非奇异是变分重构相对于CLS和k-exact重构的一个巨大的优势，因为后两者都无法保证重构矩阵的非奇异性。

线性方程组式(35)是全场单元的重构线性方程组联立组成的一个大型稀疏线性方程组，每个单元的实际依赖模板都是全场单元的集合。如果用直接法求解，那么无论如何都不能做到紧致。事实上，引入式(35)的唯一目的是证明重构矩阵的正定性。在实际求解过程中，无需组装式(35)所示的大型稀疏矩阵线性方程组。根据操作紧致性的要求，仍然采用迭代方法逐个单元求解式(33)。由于矩阵A和2D-A均是对称正定的，因此根据数值分析理论[45]，变分重构线性方程组式(33)的Block Jacobi、Block Gauss-Seidel和Block SOR(Successive Over-Relaxation)迭代都是收敛的。变分重构矩阵的优良特性不仅保证了重构矩阵的非奇异性，还保证了迭代方法的收敛性。在实际计算中，一般采用Block SOR方法求解，其迭代公式为

i=1,2,…,N

(37)

式中：ω为松弛因子。进一步研究发现，松弛因子ω取值在1.3左右的Block SOR方法谱半径最小，收敛速度最快。因此求解变分重构的迭代方法是Block SOR方法，松弛因子ω=1.3。

变分重构是一类模板紧致高精度重构方法的总称，式(29)只给出了一个具体的例子。一般来讲，构造变分重构的泛函要遵循以下原则：

1) 泛函对应的变分重构必须具有k-exact特性，这样便能够保证变分重构的精度。

2) 泛函对应的变分重构必须是紧致的，即中心单元在泛函中只与面相邻单元相关。

3) 泛函对应的变分重构矩阵必须是对称正定的。

满足条件1)～3)的重构泛函可以有无穷多种。给出一种更为通用的泛函形式，即在式(30)中，If的定义为

(38)

式中：ωv、ωs、ωv,p和ωs,p为可人为选定的权函数；ΩL和ΩR分别为左、右两侧控制体。

式(38)不仅包含IJI，还包括界面两侧控制体上的重构多项式及其各阶导数相互之间的差在控制体上的积分。通过合理确定权函数可以进一步提高变分重构的精度和效率，这是目前正在开展的研究。

2.3 多步重构

CLS重构和变分重构都是隐式重构，即使采用迭代方法求解计算量仍然很大。在第3节将介绍与隐式时间积分结合时，进一步提高隐式重构计算效率的措施。当与显式时间积分结合时，隐式重构不适于计算非定常流动。为改善紧致重构在显式时间积分情况下的计算效率，提出了一种多步重构方法。这种方法大量使用矩阵操作，不容易直观理解。简单起见只介绍一维重构，高维重构算法详见文献[28]。

以三次多项式重构为例说明多步重构的思路和实施过程。一维情况下的紧致模板为

(39)

式中：φl,i为零均值基，φ1,i=(x-xi)/h，φ2,i=(x-xi)2/h2-1/12，φ3,i=(x-xi)3/h3，其中h=Δx,Δx为网格间距。

均匀网格上单元Ωi的三次重构多项式表达式为

(40)

显然，重构多项式中有3个待定参数，而把式(18)的重构关系应用于一维情形，只能得到两个独立的重构关系：

(41)

因此，重构问题是欠定的。在紧致模板下实现高阶显式重构可通过多步方法实现。一般三次多项式重构需要分3步实现，逐一展开介绍。

1) 第1步重构

(42)

(43)

(44)

(45)

2) 第2步重构

经过第1步重构得到了每个单元对应的规范化重构关系，即式(46)。由于重构模板的紧致性要求，在第2步重构中只列出单元Ωi的紧致模板上的规范化重构关系，即

(46)

(47)

进一步，假定各单元的重构函数之间是光滑过渡的，因此根据式(47)有

(48)

以及

(49)

通过式(48)和式(49)将紧致模板中Ωi-1、Ωi+1单元上重构多项式的待定系数表示为Ωi上重构多项式待定系数的线性组合。这个过程称为延拓算法。利用这个算法，式(46)可以改写为

(50)

经过延拓运算得到的式(50)称为第2步重构的原始重构关系，式(50)的3个方程均与Ωi上的重构多项式ui(x)相关。对于一维问题，式(50)中有3个方程，原则上可以确定三次重构多项式的3个待定系数。但是对于二维和三维非结构网格而言，第2步重构的原始重构关系可能不足以确定三次重构多项式的待定系数。一般而言，无论是几维问题，多步重构的每一步比上一步提高一阶精度是可行的。在第1步重构中介绍过，第1步的重构关系足以进行线性重构，则第2步总是可以进行二次多项式重构的。为此，将式(50)改写为

(51)

(52)

(53)

根据式(52)，式(53)可以进一步记为

(54)

式(54)是第2步重构得到的规范化重构关系，有两个独立方程。

3) 第3步重构

首先列出Ωi的紧致模板上第2步重构得到的规范化重构关系，共有6个独立方程。然后采用延拓算法将紧致模板中Ωi-1、Ωi+1单元上重构多项式的待定系数表示为Ωi上重构多项式待定系数的线性组合。这样就得到了计算三次重构多项式ui(x)的6个新的原始重构关系。这6个关系足以用最小二乘法确定ui(x)中的3个待定系数，从而可以得到三次重构多项式。其具体操作与第2步类似，不再赘述。

综上所述，多步重构主要算法为部分求逆算法和延拓算法。部分求逆算法在保留高阶待定系数的情况下对低阶系数做最小二乘，可以得到新的重构关系即规范化重构关系。一般第1步重构对重构多项式一次项做部分求逆，第2步对一次和二次项做部分求逆，并以此类推到更多重构步。延拓算法延拓紧致模板上的规范化重构关系，把紧致模板中Ωi-1、Ωi+1单元上重构多项式的待定系数表示为Ωi上重构多项式待定系数的线性组合，从而将紧致模板上的规范化重构关系转化为可以计算ui(x)待定系数的新原始重构关系。多步重构实际上是在每步隐含地扩充模板的过程。例如，在第2步重构使用的规范化重构关系(即式(45))涉及Si-1、Si和Si+13个紧致模板，包含的单元为{Ωi-2,Ωi-1,Ωi,Ωi+1,Ωi+2}。然而，在每一重构步的操作遍历所有单元时，仅对每个单元紧致模板的信息进行操作，从而保证了算法的操作紧致性。

显然，3个重构步中部分求逆和延拓的操作可以在任意网格上对任意维数的问题进行。因此，多步重构的思路可以直接用于多维任意非结构网格。对于多维问题，其计算量比k-exact重构略大。如多维非结构网格的三次多项式重构需要分3步进行，其中第3步的计算量和k-exact重构类似。但是由于多步重构前两步的计算量较小，所以总的计算量比k-exact重构增加并不明显。与k-exact重构相比，多步重构的优点是基于紧致模板；与CLS重构和变分重构相比，多步重构的优势是可以灵活地采用显式和隐式时间积分。

3 紧致高精度有限体积方法其他问题的讨论

3.1 重构的实施

第2节所述隐式和显式重构过程的具体实施在于确定每个单元上的重构关系。如在开展CLS重构或变分重构且用迭代法求解时，需计算式(28)或式(37)中涉及的所有矩阵；采用显式多步重构时，也要进行类似的矩阵运算，但每步可以直接计算，无需迭代求解。无论采用哪种紧致重构，都无需组装全场的大矩阵，只需针对每个单元的重构关系进行操作。每个单元的重构关系涉及矩阵规模都比较小，对守恒变量的每个分量都是相同的，因此总体计算量不大。此外，由式(25)和式(34)可以看出，涉及的矩阵均只与网格的几何参数相关，在不进行网格自适应时，可以只在计算启动后计算一次并存储下来，从而显著提高计算效率。在计算矩阵中的元素时，一般需要进行数值积分运算，如式(25)中的

(55)

或式(34)中的

(56)

在程序设计方面，必须记录非结构网格的基本数据结构，如控制体顶点编号及坐标、每个控制体的编号及由哪些顶点组成等。此外，由于紧致重构的操作紧致性，在程序设计中只需记录和当前控制体有公共面的控制体；为方便通量计算，还需记录所有界面编号及其两侧的控制体编号。可见，在数据结构方面，紧致有限体积方法和常规的二阶精度有限体积方法完全相同。这就使可在现有二阶格心型有限体积程序基础上，于不改变数据结构的情况下引入高阶紧致重构。这给程序的发展带来了很大方便。

3.2 隐式重构提高计算效率的措施

即使采用迭代法求解，如果每次迭代到收敛，CLS重构和变分重构的计算量仍然是非常大的。因此，如何进一步提高计算效率是基于隐式重构的有限体积方法能够成功应用的关键。对于定常问题的计算，由于不关心时间推进方法收敛过程中的时间精度，可在每个时间步只执行迭代过程式(28)或式(37)一次，并让迭代和时间推进同时收敛到定常解。由于执行迭代过程式(28)或式(37) 一次的计算量和进行一次k-exact重构基本相同，因此在定常计算中，隐式重构的紧致有限体积方法计算量和基于传统k-exact重构的有限体积方法基本相同。图3为定常问题基于CLS重构和k-exact重构的有限体积方法收敛速度比较，CLSFV代表基于CLS重构的FV方法，可见二者基本相同[44]。

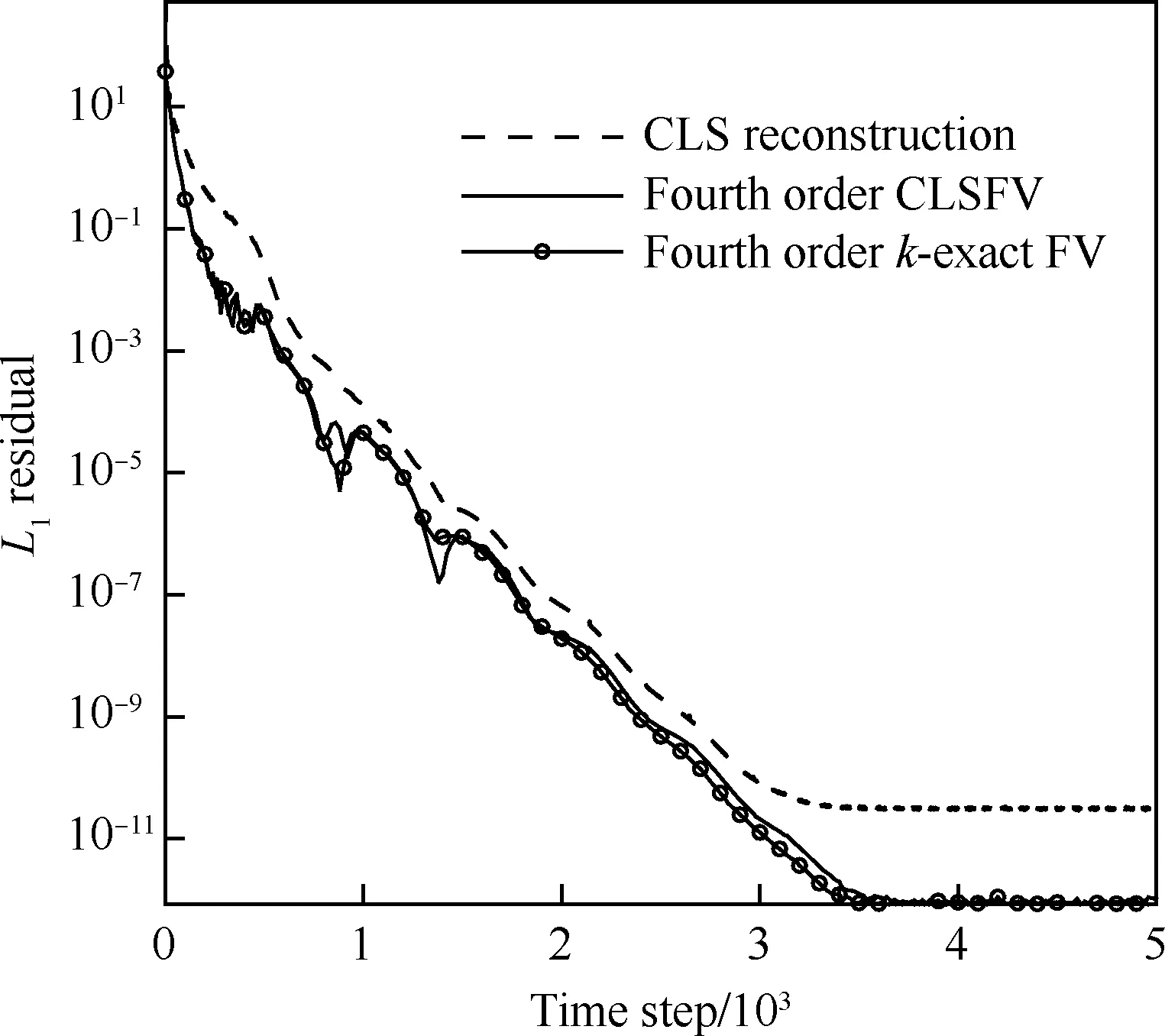
图3 定常问题基于CLS重构和k-exact重构的FV方法收敛速度比较[44]Fig.3 Comparison of convergence speeds of CLS reconstruction and k-exact reconstruction FV schemes in steady flow[44]

在求解非定常问题时，为提高计算效率，隐式重构一般和双时间步(Dual Time-stepping)隐式格式联合使用。由于流体力学基本方程常常是高度非线性的，在非定常时间推进过程中必须引入迭代求解过程，即使使用常规重构方法时也是如此。双时间步隐式方法就是常见的一种迭代过程,此方法把一个物理时间步的推进过程分为虚拟时间步的多次内迭代，使迭代解逐步趋近非定常真解。利用这个性质提出了一种重构和双时间步耦合迭代解法[25]，在每次内迭代过程中，迭代过程式(28) 或式(37)也只执行一次。随着内迭代的进行，重构迭代和时间推进迭代同步收敛。显然，这种方法的计算量也和基于传统k-exact重构的双时间隐式有限体积方法相当。通过上述分析可以确信，隐式重构有限体积方法在一定条件下仍然可以达到很高的计算效率。事实上，紧致重构求解的是一个线性方程组，而虚拟时间步内迭代求解的是一个非线性方程组。数值实验表明，紧致重构的收敛速度会比虚拟时间步内迭代的收敛速度快得多。图4为静态CLS重构收敛速度和时间推进残差收敛速度的比较，可以清楚地看到这一现象[44]。

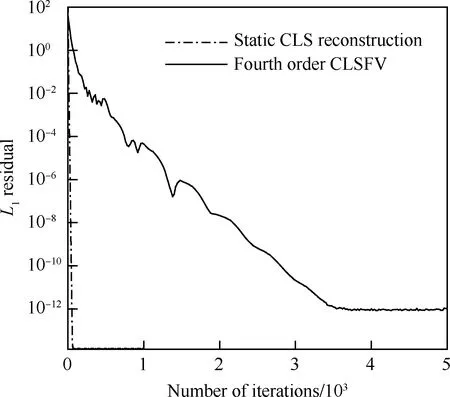
图4 静态CLS重构和双时间步迭代残差收敛速度比较[44]Fig.4 Comparison of residual convergence speeds of static CLS reconstruction and dual-time stepping iteration[44]

3.3 边界处理

边界处理是影响数值计算精度的重要因素，主要讨论重构过程中的边界处理。物理边界条件的实施精度依赖于边界附近重构的精度，一般直接作用于数值通量，和常规有限体积方法相同。3种重构方法的边界处理有一些不同的特点。在边界附近的典型紧致重构模板如图5所示。

对于CLS重构而言，物理边界(非周期边界)单元要进行特殊处理。这是因为物理边界单元的面相邻单元个数至少比内点单元少一个，造成重构线性方程个数的减少。如对于图5所示的边界单元，有2个面相邻单元，如果仿照内点单元取M=k-1，对于CLS重构，式(27)中与Ωj3有关的项不再存在。因此，二维三次多项式重构时，有9个 待定系数，重构关系中有12个方程。虽然方程个数仍然大于未知量个数，但数值测试表明这种边界重构格式不稳定。即使将守恒导数的阶次调到最大，即M=k，获得了20个方程，也很难获得稳定的边界重构格式。但数值测试结果表明，将边界单元的重构格式精度降低一阶便可以得到稳定的边界重构格式。根据Gustafsson[46]的分析，边界单元重构格式精度降低一阶不会造成整体格式精度阶数的降低。测试结果表明，边界单元重构精度降低一阶时，用L1误差范数衡量，整体格式勉强达到理论精度阶数；用L∞误差范数衡量，整体格式精度会降低一阶。

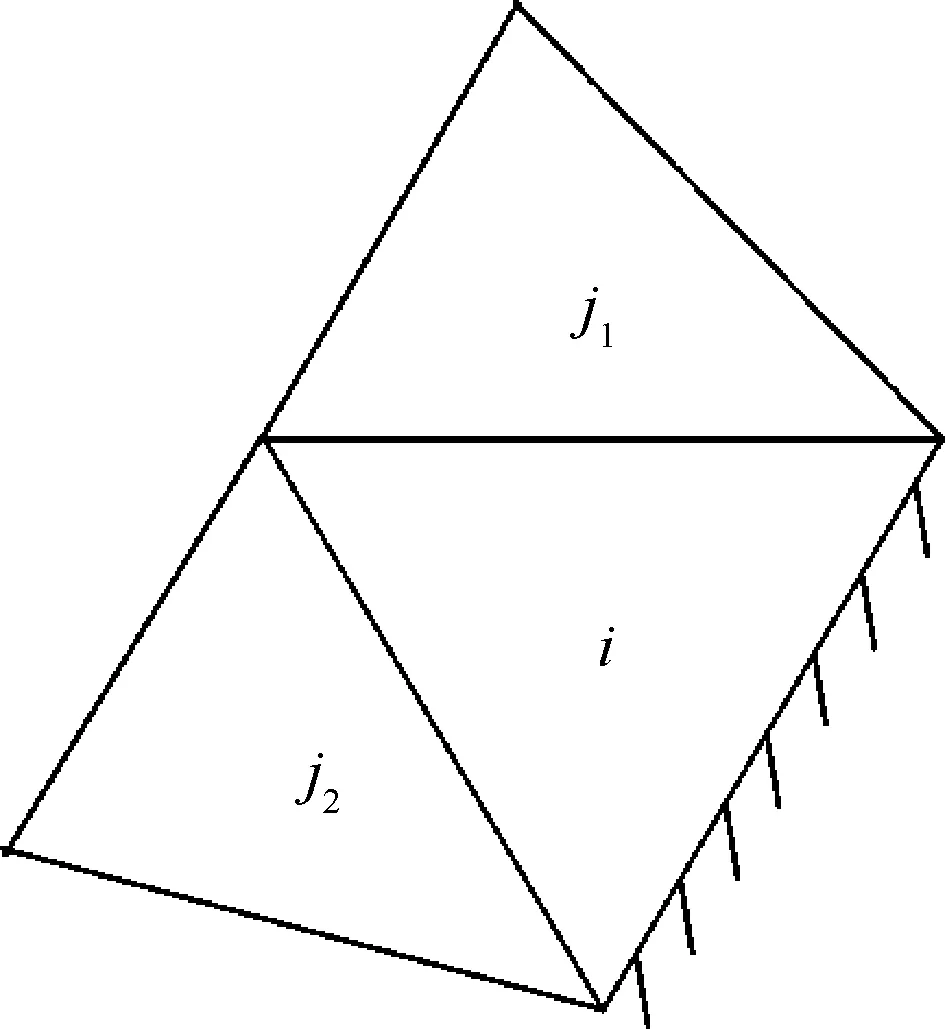
图5 边界单元的紧致重构模板Fig.5 Compact reconstruction stencil of boundary cells

多步重构和CLS重构面临的问题基本相同。特别是当边界单元只有一个面相邻内部单元的情况，有可能出现多步重构的第1或第2步原始重构关系数量不够的情况。为解决这个问题，提出一种边界单元的异步重构方案，即第m步重构先对内部单元进行，在得到内部单元的规范化重构关系后，再把其规范重构关系延拓到面相邻边界单元；最后利用这些规范化重构关系进行边界单元的第m步重构。对于多步重构，边界单元重构阶数也要比内点低一阶。

在处理黏性流动的无滑移边界条件时，CLS重构和多步重构可把无滑移条件作为一个重构关系，与其他重构关系同时进行最小二乘计算；也可把无滑移条件当作约束条件，采用约束最小二乘方法求解。

在边界处理方面，变分重构有明显优势。其最突出的优势是可以达到与内点一致的精度，无需降阶。另一个优势是可以通过引入边界泛函考虑物理边界条件的影响。以式(30)的泛函为例，当考虑边界条件时，式(30)改写为

(57)

式中：Ibf为表征边界条件的IJI；Nbf为物理边界面的总数。以无滑移等温固壁边界条件和对称边界条件为例介绍边界面的IJI构造方法。对于无滑移等温固壁，守恒变量U的边界IJI为

(58)

式中：dbf为边界面bf所属的单元中心到边界面bf的中心的距离；下标L和bf分别代表边界界面内侧和外侧的物理量，外侧的物理量由边界条件确定。对于壁面温度为Twall的静止固壁，守恒变量在边界面上的值计算公式为

(59)

式中：ρ、E、cp、u、γ和v分别为密度、总能、定压比热、比热比和两个方向上的速度分量。

3.4 激波捕捉

良好的激波捕捉性能是对可压缩流动求解器的基本要求，对于高阶格式一般需要引入限制器或非线性人工黏性抑制激波附近的振荡。对有限体积和DG等方法的限制器开展了比较系统的研究[47-50]。对于紧致高精度有限体积方法，推荐的限制器是WBAP(Weighted Biased Averaging Procedure)限制器[48]。WBAP限制器具有如下7个优点：① 光滑区保精度；② 基于紧致模板；③ 直 接作用于重构多项式系数，无需数值积分，计算效率较高；④ 通过采用二次重构技术，无需在多个模板上开展重构，计算效率显著优于WENO格式；⑤ 适用于结构和非结构网格；⑥ 通过采用逐次限制的方法可对任意阶精度重构进行限制；⑦ 在一定条件下可退化为TVD限制器或满足极大值原理，具有良好的抑制振荡的能力。其具体原理和实施过程见文献[48]，不再赘述。WBAP限制器和这3种紧致重构算法都可以较好地结合，得到的有限体积格式具有很好的激波捕捉能力。图6为三次CLS重构有限体积格式(四阶精度)计算复杂激波绕射的结果。

图6 正激波绕过复杂几何形状障碍物(t=1.5时刻障碍物附近的密度分布)Fig.6 Normal shock wave flows past obstacle with complex geometry (density distribution near obstacle at t=1.5)

3.5 高阶网格

复杂几何外形(如飞机机身)通常包含曲面边界，如用直边网格表示曲面边界，会过滤掉高阶曲面信息，从而降低高阶数值方法的精度。对于DG等方法，可能计算出非物理解。有限体积方法虽然一般不会出现非物理解，但整体精度会下降。处理曲面边界的实用方法是采用高阶曲面或曲线网格，目前已有一些高阶网格的生成方法[51]。当采用高阶网格时，必须采用参数变换的方法计算式(55)、式(56)的数值积分。发展了直角参数坐标系下建立插值基函数的一般方法，并给出高阶三角形、四边形、四面体、三棱柱和六面体单元的参数变换公式。借助于参数变换公式可求出数值积分点的物理坐标和Jacobi值进行数值积分。计算金字塔单元的体积分时，最佳方案是将金字塔单元剖成两个四面体，金字塔单元的体积分就等于这两个四面体单元的体积分之和。表2给出了参数变换对应的网格类型及总控制点数。图7为二维三角形二次网格及其6个控制点(黑圆点)，图8为三维四面体二次网格及其10个控制点。对于坐标x，参数变换公式可以一般地写为

图7 二次三角形单元TRI_6Fig.7 Quadratic triangular cell TRI_6

图8 二次四面体单元TETRA_10Fig.8 Quadratic tetrahedron cell TETRA_10

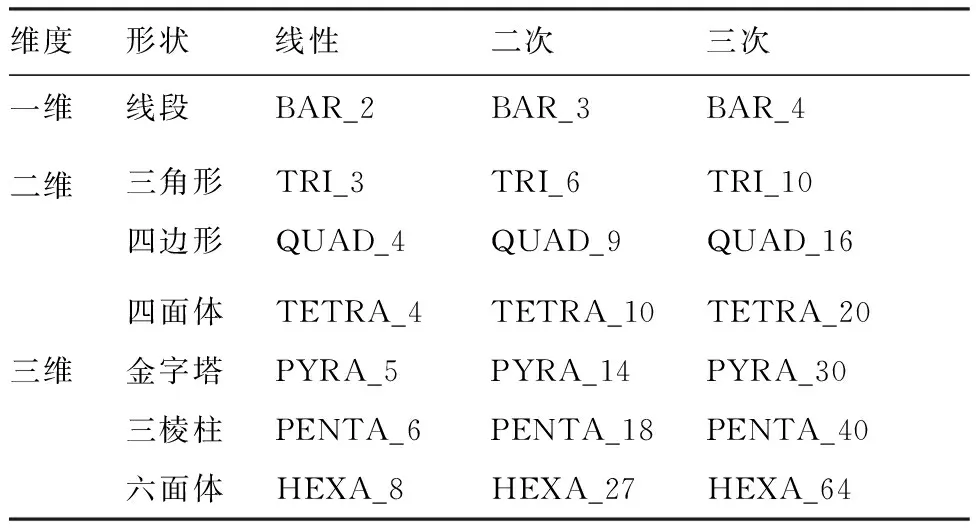
表2 网格单元类型及其控制点数Table 2 Types of grid units and number of reference points

(60)

式中：ξ、η和ζ为参数坐标，取值范围均为[0,1]；xi为控制点笛卡尔坐标；vi(ξ,η,ζ)为第i个控制点的Lagrange插值基函数；nc为控制点的总数。

举例说明基函数vi(ξ,η,ζ)的表达式。对于二维三角形二次网格，有v1=(ξ+η-1)(2ξ+2η-1)，v2=ξ(2ξ-1)，v3=η(2η-1)，v4=-4ξ(ξ+η-1)，v5=4ξη，v6=-4η(ξ+η-1)。

对于三维四面体二次网格，有v1=(-1+ζ+η+ξ)(-1+2ζ+2η+2ξ)，v2=ξ(-1+2ξ)，v3=η(-1+2η)，v4=ζ(-1+2ζ)，v5=-4ξ(-1+ζ+η+ξ)，v6=4ηξ，v7=-4η(-1+ζ+η+ξ)，v8=-4ζ(-1+ζ+η+ξ)，v9=4ζξ，v10=4ζη。

其他情形见文献[44]。

3.6 时间推进

在求解定常问题时，紧致重构可以和任意时间推进格式相结合。当求解非定常问题时，显式多步重构可以和任意显式和隐式时间推进格式相结合。隐式重构即CLS重构和变分重构，只有和隐式双时间步格式相结合使用才能实现高求解效率。此外，在求解非定常问题时，高精度有限体积方法在时间方向也要达到高阶精度。例如，当采用三次多项式紧致重构时，空间为四阶精度，则时间离散格式也应达到四阶精度。三次CLS和变分重构下，采用的时间离散格式为多步隐式Runge-Kutta方法，具体为三步四阶精度的SDIRK4方法[52]。其具体实施步骤如下。

(61)

三步四阶精度SDIRK4方法的离散公式为

(62)

式中：

(63)

其中：bα为向量；aαβ为矩阵。矩阵aαβ和向量bα各元素的值见表3，ζ=0.128 886 400 515。

表3 三步四阶SDIRK4方法的Butcher表Table 3 Butcher table of 3-stage p4 SDIRK4 method

求解式(63)时，在其左端加一个虚拟时间项，采用双时间步方法迭代求解。迭代方法为LU-SGS(Lower-Upper Symmetric Gauss-Seidel)或GMRES(Generalized Minimum RESidual)+LU-SGS方法。

3.7 计算精度和效率

按照式(1)的计算效率定义，比较合理的计算精度和效率的衡量标准是在数值误差一定时，计算时间越短越好；或计算时间一定时，数值误差越小越好。按照这一标准，无论哪一种重构方法，高阶格式的性能都显著优于二阶格式。对于同样精度格式之间的比较，采用二维等熵涡问题进行分析。等熵涡问题的计算网格见图9。将网格逐次加密进行求解。图10(a)[25]表明，同阶的CLS有限体积格式明显优于k-exact格式；图10(b)[26]表明，在计算网格较密时，变分有限体积(Variational Finite Volume，VFV)格式计算效率优于CLS有限体积格式，网格较少时则相反；图10(c)[27]表明，多步重构(MSR)有限体积格式和k-exact格式基本相当，其主要优势在于模板的紧致性。

图9 二维等熵涡问题的计算网格Fig.9 Computing grid of isentropic vortex problem in 2D

图10 等熵涡问题计算效率比较Fig.10 Comparison of computational efficiency of isentropic vortex problem

对于有激波的三维问题计算，高阶紧致有限体积也取得了很好的结果。图11[44]为四阶变分有限体积格式计算出ONERA-M6跨声速绕流问题的马赫数等值线，计算网格由约100万四面体网格组成。将变分有限体积方法应用于求解RANS方程，图12[43]为四阶变分有限体积格式采用SA模式计算平板湍流边界层的速度剖面，与其进行比较的是网格数为高阶格式网格16倍时用CFL3D软件得到的结果,可见二者精度基本相当。

图11 四阶VFV格式计算出的ONERA-M6跨声速绕流问题马赫数等值线[44]Fig.11 Contours of Mach number in transonic flow past ONERA-M6 airfoil computed by fourth order VFV scheme[44]

图12 四阶VFV格式得到的湍流平板边界层问题速度剖面[43]Fig.12 Velocity profile in turbulence boundary layer problem computed by fourth order VFV scheme[43]

3.8 发展及推广

由于变分重构非奇异的优良特性，目前主要发展的是基于变分重构的非结构网格高精度紧致有限体积方法。

潘建华等[53]将自适应网格技术引入变分重构有限体积方法，显著提高了计算效率。最近，进一步研究了非定常流动网格自适应准则问题，提出了基于亚网格能量耗散的自适应算法。图13(a)和图13(b)是采用这种准则计算三维圆柱湍流的网格及涡量等值线(只显示了一个横截面)，初步结果表明，这种方法比基于涡量的网格自适应准则效果更好。

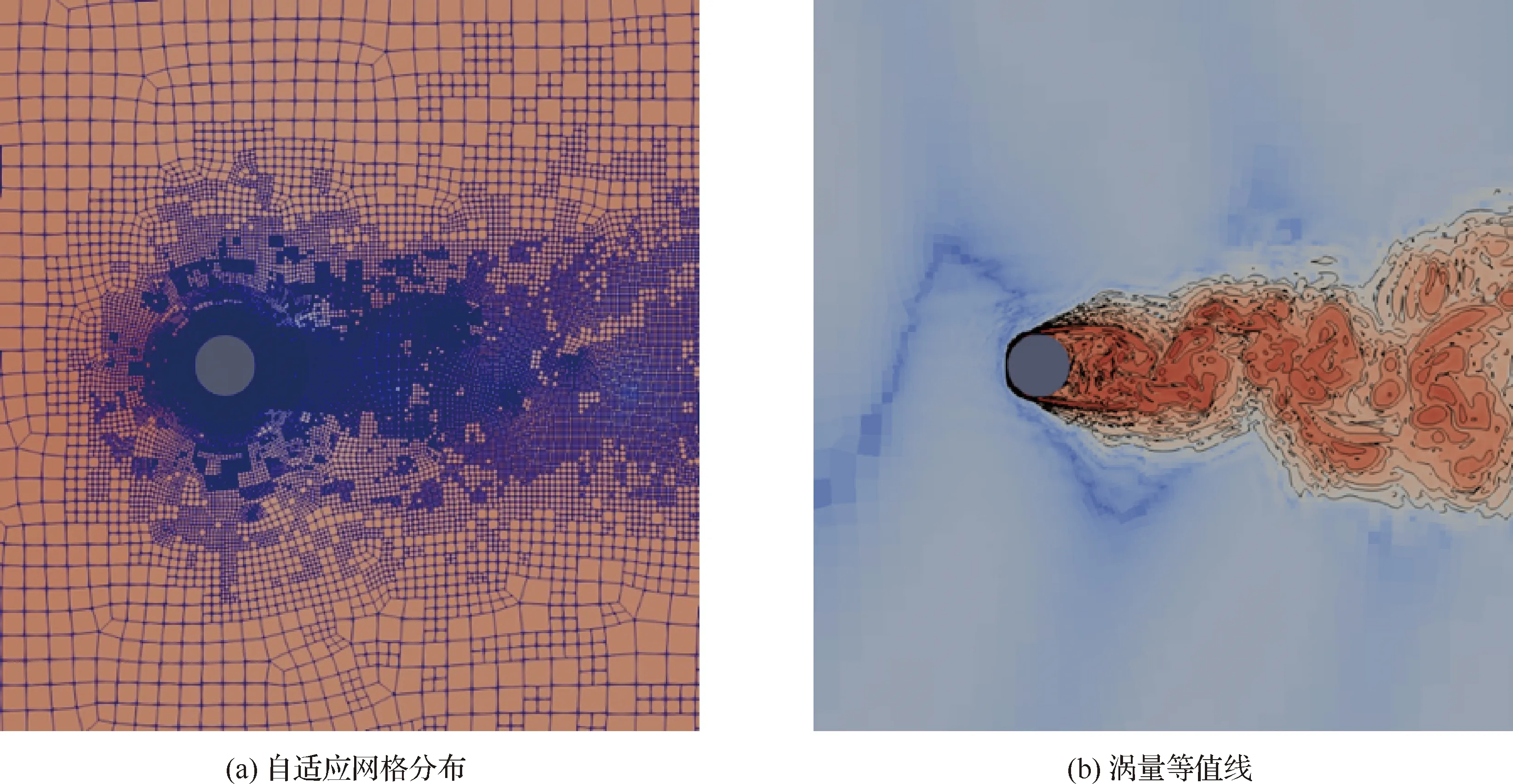
图13 四阶VFV格式得到的圆柱绕流问题自适应网格分布和涡量等值线Fig.13 Distribution of adaptive grids and contours of vorticity in flow past cylinder computed by fourth order VFV scheme

黄乾旻等[54]将变分重构有限体积方法推广到求解非守恒方程，通过引入对流重构方法克服了常规方法的数值稳定性问题；他还研究了大长宽比网格上变分重构的构造以及RANS模式的保正问题，显著提高了高精度有限体积方法RANS模拟的精度和鲁棒性。图14为采用SA湍流模式计算30P30N高升力构型的湍流流动的计算结果。结果表明，通过改进变分重构泛函和湍流模型的保正处理，变分重构高精度有限体积法可实现RANS方程鲁棒稳定的高精度求解，不会出现负的湍流黏性系数，且壁面摩阻系数比二阶格式更为准确。

图14 四阶VFV格式得到的16°攻角下30P30N高升力构型参数Fig.14 Parameter of 30P30N high lift configuration at angle of attack of 16° computed by fourth order VFV scheme

变分重构算法也促进了其他非结构网格高精度格式的发展。如把变分重构作为重构DG方法的重构算法取得了很好的结果，有效解决了多维重构的稳定性问题，代表性工作见文献[55-56]。又如Tamaki和Imamura[57]在CLS重构的启发下，提出了迭代最小二乘重构方法。Nishikawa[58]在变分重构的启发下提出了隐式Green-Gauss梯度重构方法。变分重构方法还将作为非结构网格高精度有限体积方法的方案之一，在国家数值风洞工程中继续得到发展及应用。

4 结 论

紧致重构技术是为解决非结构网格高精度有限体积方法重构模板巨大这一瓶颈问题而提出的。在概念层面，提出了操作紧致性这一重要概念，即不要求实际上采用的模板是紧致的，只要求在数值求解过程中所有的数据结构和计算操作都只用到紧致模板中的信息。这一概念创新极大扩展了构造重构算法的多样性，使发展高阶紧致重构成为可能。

在方法层面，提出了CLS、变分、多步等紧致重构方法。从实际性能角度看，变分重构非奇异、计算效率高、边界不降阶，总体上是3种方法中最优的。CLS重构可以看作k-exact重构的推广，比较简单，性能上不如变分重构，但优于多步重构。变分和CLS重构是隐式重构，在计算非定常流动时必须和隐式双时间步方法结合才能达到较高计算效率；而多步重构无须迭代求解，可以和任意显式和隐式时间推进格式结合，有效计算非定常流动。因此，几种紧致重构方法各有特点，共同构成了非结构网格高精度有限体积方法的基础算法。

在实施层面，综述了在具体实施方案、边界处理、激波捕捉、高阶网格、时间推进等方面一些需要注意的问题。

在应用层面，所发展的方法已经成功地应用于一系列二维、三维，有黏、无黏，层流和湍流流动的模拟，在计算精度和计算效率等方面相对于二阶精度有限体积方法显示出了明显的优势。

紧致重构有限体积方法彻底解决了常规有限体积方法的大模板问题，为非结构网格高精度有限体积方法的发展提供了广阔空间。近期的一些新进展表明，紧致高精度有限体积方法是一种有发展前途的新方法。