基于ARMA模型的股票价格的分析及预测

王 莹

（上海工程技术大学 管理学院，上海 201620）

一、引言

一直以来，股票市场在金融领域中有着举足轻重的地位。股票价格的波动能够在一定程度上反映一个国家经济周期的变化。尤其作为权重股的银行股，其价格波动对于整个股市的变化趋势有着重要的影响[1]。而股票价格往往对时间因素非常敏感，所以建立时间序列模型能够有效地对股票价格进行分析及预测[2]。常用的时间序列预测方法有自回归（AR）模型、移动平均（MA）模型和自回归移动平均（ARMA）模型[3]。本文将运用ARMA模型对中国银行股票开盘价历史数据进行拟合分析，并对未来三天的开盘价进行预测。

二、模型的介绍及建模步骤

（一）ARMA模型的介绍

ARMA模型是由AR自回归过程和MA移动平均过程组成的自回归移动平均模型，是时间序列分析模型的一种，其基本思想是通过揭示历史时间序列的运行规律，从而对未来的事物发展进行预测。在ARMA（p，q）模型中，p为自回归阶数，q为移动平均阶数。

一般的ARMA（p，q）模型的形式可以表示为：

式（1）中，{εt}是白噪声序列，AR和MA模型都是特殊的ARMA（p，q）模型，当p=0 时，ARMA（0，q）就是MA（q）；当q=0 时，ARMA（p，0）就是AR（p）。当时间序列不平稳时，不能直接运用ARMA模型，而是需经过差分或取对数等处理后，形成一个新的平稳的时间序列[4]。

对于非平稳时间序列，可以拟合模型ARIMA（p，d，q），其方程式如下：

其中：d为差分阶数；

B为滞后算子；

特别地，当d=0 时，ARIMA模型就是ARIMA模型。

（二）ARMA模型的定阶方法

ARMA模型的定阶方法主要是通过观察自相关图和偏自相关图，根据其系数的相关特性来判断阶数。若AC是拖尾的，PAC是p阶截尾的，则选择AR（p）模型；若PAC是拖尾的，AC是q阶截尾的，则选择MA（q）模型；若AC和PAC都表现为拖尾性，则选择ARMA（p，q）模型，然后通过模型的参数检验，进一步判断p、q的阶数。

但由于样本具有随机性，相关系数并不会表现出完美截尾的情况，通常会呈现出小值振荡的情况，这就给模型的定阶带来了一定的困难。根据以往的经验，如果样本自相关系数或偏自相关系数在初始的d阶明显大于两倍标准差范围，其后几乎95%的自相关系数都在两倍标准差范围内，并且由非零自相关系数衰减为小值波动的过程非常突然。这时可以视为自相关系数或偏自相关系数d阶截尾[5]。

（三）ARMA模型的平稳性检验——单位根检验

单位根检验是通过检验特征根距离单位圆的位置来判断序列的平稳性的。通常采用的是ADF检验，ADF检验主要有三种类型：无趋势无截距、有截距无趋势、有截距有趋势。形式如下：ADF 检验主要步骤如下：首先进行第三种情形的检验，若拒绝原假设，则检验时间趋势项系数的显著性，若显著性拒绝原假设，则该序列为趋势平稳。反之进行第二种情形的检验，若拒绝原假设，则检验截距项系数的显著性，若显著性拒绝原假设，则为含截距项平稳；若不拒绝原假设，则进行第一种情形的检验，若拒绝原假设，则该序列为不含截距项和时间趋势项平稳。若三种情形均不能拒绝原假设，则应综合第一种和第二种的AIC、SC、HQ 判断选择哪种情形下的单位根检验。

三、股票价格预测的实证分析

本文通过东方财富网选取了中国银行（601988）2019 年8 月20 日至2020 年8 月21 日的股票日开盘价数据，一共245 个样本。运用Eviews 10 软件进行建模分析对未来三天的股价进行预测。

（一）原始数据的平稳性检验

1.时序图检验。首先对数据的平稳性进行判断：将原始数据输入Eviews 软件，生成时间序列图（见图1）。平稳时间序列的图像始终围绕着某一个值上下波动且波动范围有界，没有明显的趋势和周期性。由图1 所示，序列趋势不太明显，存在上下波动的状态，可以初步判断中国银行股票开盘价大致平稳的。

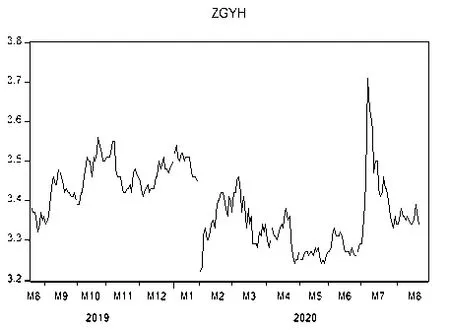
图1 中国银行股票开盘价时序图

2.单位根（ADF）检验。为了准确判断原始序列是否平稳，进一步对原始数据进行三种情况下ADF检验（结果如图2、图3、图4 所示），其ADF test statistic值分别为-3.410 698、-2.954 879 和-0.152 588，P值分别为0.052 3、0.040 7、0.630 1，经分析发现三种情况中，在有截距情况下的单位根检验的P值小于0.05，拒绝原假设，可以认为原始数据为平稳时间序列。

图2 有截距有趋势项的单位根检验

图3 有截距的单位根检验

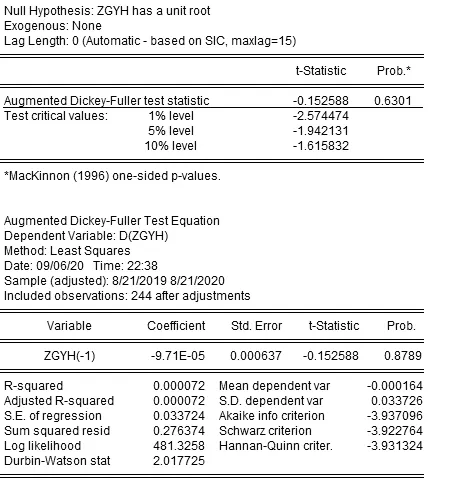
图4 无截距无趋势项的单位根检验

（二）模型的识别

在对时间序列数据进行平稳性检验之后，我们需要根据样本相关系数的拖尾性和截尾性来识别模型的类型，并确定滞后阶数p和q的值。

观察样本自相关图和偏自相关图（见图5），其中p值均为0，说明原始序列为平稳非白噪声序列，可以进行模型拟合。由图5 可知，序列自相关系数缓慢衰减且过程相当连续，呈现拖尾性质。而偏自相关系数除了滞后一阶的数值较大，其他数值均在两倍标准差范围内作小值随机波动，并且相关系数衰减的过程非常突然，所以可以判断偏自相关系数为一阶截尾。综上所述，可以考虑拟合模型为AR（1）。

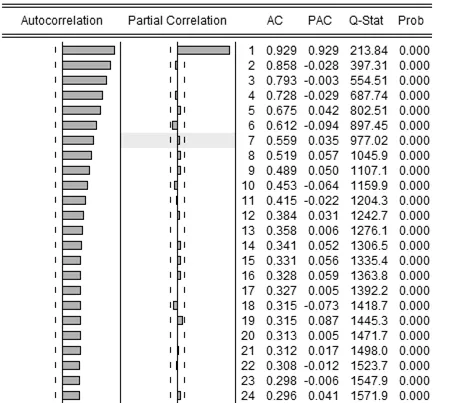
图5 序列自相关图和偏自相关图

（三）模型的建立与参数估计

根据上文，选择AR（1）模型作为最佳预测模型进行拟合，如图6 所示，根据图中结果，模型AR（1）对应的p值为0，小于0.05，模型参数显著有效。进行参数估计，可以写出表达式为：xt=0.999950xt-1+εt，其中εt为残差序列。

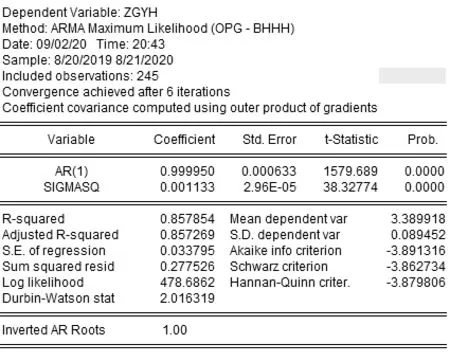
图6 AR（1）模型拟合

（四）模型的显著性检验

参数估计完成后，还需要对模型进行显著性检验。目的是检验模型是否充分的提取了时间序列中的信息，即残差序列是否为白噪声序列。若残差序列为非白噪声序列，那就说明残差序列中还有残留的相关信息未被提取，还需对模型进一步完善。

对拟合AR（1）模型进行残差检验，结果如图7 所示，延迟6 阶和12 阶的Q统计量值分别为4.150 5和8.322 3，P值分别为0.528 和0.684。由于P 值大于显著性水平α，所以该序列不能拒绝原假设，即残差序列为白噪声序列，模型显著有效。事实上，DW检验同样可以判断残差序列的自相关性。图6 中DW 检验值为2.016 319，十分接近2，因此可以认为残差序列不具有自相关性。

图7 残差序列自相关图

从图8 的模型拟合效果图来看，拟合值和真实值还是十分贴合的，残差也为围绕着某个值随机波动，残差信息提取的较为充分。

图8 模型拟合效果图

（五）模型的预测分析

最后用拟合的ARMA模型对中国银行股票未来三天的开盘价进行预测，并将预测结果与真实数据进行对比，结果如表1 所示。

表1 中国银行未来三天股价的预测结果

根据表1，用模型预测出的股票价格与真实价格较为接近，误差较小，说明ARMA模型预测股票价格的效果比较理想。但由于影响股票长期价格的因素较多，在利用ARMA模型进行时间跨度大的预测时，误差也随之增大，因此本模型更适合于股票价格的短期预测[6]。

四、结语

股票价格预测一直是一个值得关注的问题。本文采用ARMA模型对中国银行股票开盘价进行预测的实证，表明了时间序列模型对于股票价格的短期预测是可行的。模型对价格信息提取比较充分，拟合效果较好，预测值与真实值的误差相对较小。但由于下一期的预测是根据上一期的预测值计算的，因此产生的累计误差将越来越大。对于股票价格的长期预测来说，ARMA模型的预测效果会大大降低。而且股票价格的长期趋势受到行业政策等环境因素的影响较大，而短期预测受到的干扰因素的影响较小。因此投资者应该选择模型的短期预测值作为投资决策的参考。