ESTAR模型的单位根检验统计量及其功效比较

赵春艳，南士敬

（西安交通大学 经济与金融学院，西安 710061）

0 引言

指数平滑转换自回归模型（ESTAR）是STAR系列模型中的一种，它的一阶形式如式（1）所示：

其中，γ称为斜率参数，代表两种机制的转换速度；st是转换变量，它是导致yt由一种机制转换为另一种机制的变量，单变量分析中，st可以选择 yt-d（d为滞后期），也可以选择时间项t；c称为位置参数，是导致yt机制转换的具体位置。进一步研究发现，ESTAR模型的最大特点体现在其转换函数 G(·)上，参数 γ、c 决定了 G(·)的变化情况。γ越大，yt变化的速度越快。当 st→+∞和st→-∞ 时，均有G(·)=1，ESTAR模型变成普通线性AR模型，在转折点 c处，G(·)=0，因此，ESTAR模型中存在一个外制度和一个内制度,st→±∞，对应的是外制度，st→c时，对应内制度。

ESTAR模型常用来描述汇率偏离其购买力平价的行为，也称为均值回复。由于交易成本的存在，汇率会在不同机制间转换。当汇率从均衡汇率有一个小的偏离时，商品套利的利润不能弥补交易中必要的成本，这意味着在均衡汇率水平附近有较小的偏离时，汇率没有回到其均值水平的倾向[1]。过了这个偏离区间，商品套利能获利，这使得汇率水平能回到其均值水平。这里的均值水平就是位置参数c，因此，在c附近以及远离c的区间，汇率波动的行为是有差异的。

同STAR模型的其它形式一样，ESTAR模型建模前要识别序列的平稳性，本文旨在提出对ESTAR模型进行单位根检验的统计量，并对其功效进行检验和比较。

1 文献综述

ESTAR模型作为一种非线性模型，数据的平稳性问题是与其线性检验相联系的，数据的平稳性决定了线性检验统计量的分布，其平稳性的检验尚在争论中。一类平稳性检验是利用传统的ADF检验，在线性AR模型中进行[2]。这些文献都是先对序列建立AR模型，并在其中进行单位根检验，若单位根存在，则再用所提到的非标准统计量进行线性检验[3]。这类研究利用ADF统计量检验ESTAR模型数据的平稳性，由此可以推测，它们对于ESTAR模型数据平稳性的含义同线性模型数据平稳性的含义是相同的。

与上述研究不同，另一种平稳性检验是在非线性模型中进行的，而且提出了不同于线性模型平稳性的概念。Kapetanios等（2003）以一阶ESTAR模型为例，提出关于ESTAR模型的平稳性概念，即整体平稳、中间单位根的概念[4]。设{yt}是均值为零的随机过程，适合ESTAR模型，如式（3）所示。

检验的统计量如式（8）所示，在单位根条件下，tNL统计量的分布是非标准的。接受H0，序列是线性单位根过程；接受H1，序列是有单位根的ESTAR模型。

Kapetanios等（2003）在研究时，假设ESTAR模型自然地在序列的中间区域存在单位根，这样其应用会受到限制，并且所谓的单位根检验其实是单位根条件下的线性检验而并非非线性单位根检验。

Kilic（2011）同样研究了ESTAR模型的单位根检验问题，检验的模型形式同式（6）。只是与Kapetanios等（2003）不同的是，由于γ未知，参数δ无法估计，为解决这个问题，Kilic（2011）建议在参数γ的空间中取可能的t值的最小值，提出检验统计量为：

其中，Sst是st的样本标准差，γ在st的样本标准差构成的区间中搜索，γ的每个值对应有相应的δ^及t值，最小的t值即为ESTAR单位根检验的统计量值。[5]

现在我们分析前文的两条研究线索。第一条研究线索中的单位根检验是在线性AR模型中用ADF统计量进行检验的，这意味着他们认为，STAR模型的平稳性同线性模型的平稳性是一样的。我们认为非线性模型的平稳性同线性模型是不一样的，此时存在的问题是，序列本身适合的是非线性模型，而建立线性模型对其进行单位根检验，这有可能降低检验的功效[6]。

第二条研究线索是Kapetanios等（2003）、Kilic（2011）等的研究，他们的单位根检验在非线性ESTAR模型中进行，而且提出了不同于线性模型的平稳性概念，只是在检验中，直接假定单位根存在，并没有进行检验。

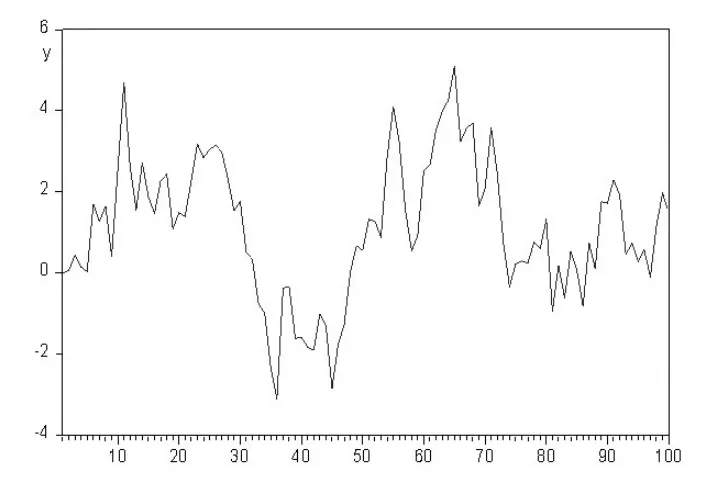
图1 φ1=1，θ1=-1.5，γ=0.01

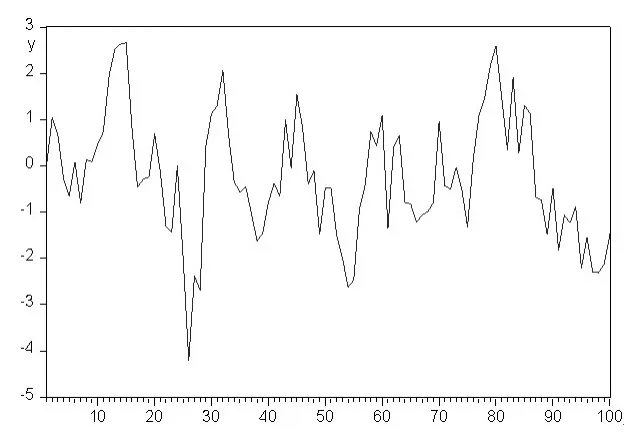
图2 φ1=0.8，θ1=-0.3，γ=0.05

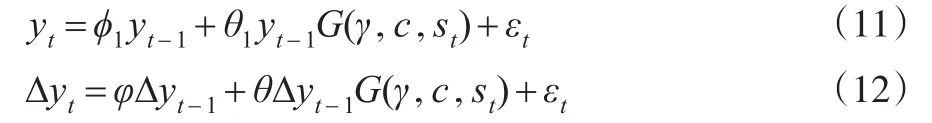
因此，我们认为ESTAR模型中，式（1）中φ1是否等于1需要检验。

鉴于此，本文以一阶ESTAR模型为例，说明在其中进行单位根检验的问题，寻找适合非线性模型单位根检验的统计量及其分布。

2 ESTAR模型的单位根检验统计量

由于ESTAR模型中有非线性函数，不易进行参数估计，人们提出用泰勒展式替代原模型。在数学上，二阶泰勒展式能近似逼近ESTAR模型，这要比Kapetanios等（2003）的一阶泰勒展式更接近ESTAR模型。Dijk（2000）也提到用ESTAR模型的二阶泰勒展式进行线性检验[9]。因此，本文用ESTAR模型的二阶泰勒展式进行单位根检验，假定转换变量st为 yt-1，以一阶ESTAR模型为例进行。ESTAR模型的二阶泰勒展式为式（13）：

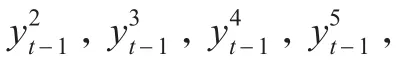
接下来，运用蒙特卡洛试验（20000次）得到t统计量的临界值如表1所示，由于小样本时，参数估计往往会存在奇异矩阵，为了保证结果的稳定性，本文只给出了大样本的临界值。从表1可以发现，样本容量对于t统计量临界值的影响并不大。在给定的显著性水平下，当t统计量值小于tα时，拒绝H0，说明序列是平稳的；当t统计量值大于tα时，接受H0，即序列存在单位根。与传统单位根检验的DF统计量的临界值相比，我们发现，非线性检验中的t统计量在相同概率下的临界值比DF统计量大，只有当样本量趋于无穷时，两个统计量的临界值才趋于相等。

表1 t统计量的临界值

3 TAR模型单位根检验统计量的功效比较

为了验证本文提到的t统计量检验ESTAR模型中单位根的功效，我们用蒙特卡洛试验进行检验，并且与DF单位根检验统计量和Kapetanios等（2003）提出的tNL统计量进行比较。本试验的目的是：数据本身是按照有单位根的模型（1）生成的，现在考察本文提出的t统计量，传统单位根检验的DF统计量以及Kapetanios等（2003）提出的tNL统计量能否真正检验出序列的平稳性及其各自的功效。

具体进行蒙特卡洛试验时，要求模型（1）中：

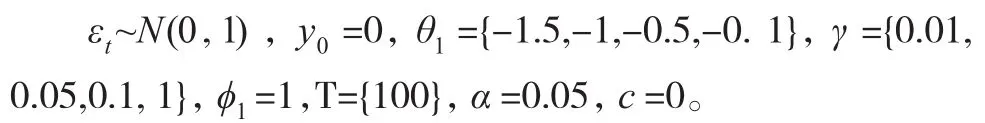
各参数所赋的值同Kapetanios等（2003）的完全相同[4]，这样可以相互比较。模拟产生数据后，分别对其拟合模型（13）、模型（6）和AR（1），并分别计算相应模型的t统计量、tNL统计量及DF统计量，试验次数为20000次。t统计量和DF统计量的检验功效用它们的零假设接受概率来表示，也就是20000个t值当中，大于临界值（存在单位根）的个数所占的比重，因为就序列的生成过程来看，序列是按模型（1）生成的有非线性特征、存在单位根的序列，如果接受单位根的原假设，则表明该统计量能检验出单位根，检验的功效高，因此，接受概率越高，则检验功效越高。Kapetanios等（2003）的tNL统计量功效用零假设的拒绝概率表示[4]，因为式（5）中的H0表示线性单位根过程，而H1表示有单位根的ESTAR模型。为便于比较，我们将Kapetanios等（2003）的试验结果放在DF统计量及tNL统计量概率值下面的括号内，只是DF统计量的概率值做了处理，没有用拒绝H0的概率而是用接受H0的概率表示功效，因为接受H0才表示其能检测出单位根。试验的结果如表2所示：

表2 非平稳的ESTAR序列的单位根检验功效比较

从表2中可以看出：

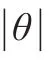
图3 φ1=1，θ1=-0.1，γ=0.01

4 结论

（1）ESTAR模型的单位根检验在其二阶泰勒展式中进行，本文提出用参数的t统计量进行检验，并给出其极限分布和临界值。

（2）通过给参数赋值产生模拟数据，用t统计量、tNL统计量及DF统计量同时对数据进行单位根检验。结果显示，DF统计量检验功效最低，t统计量与tNL统计量检验功效接近，但前者的稳定性高于后者。

[1]张卫平.购买力平价非线性检验方法的进展回顾及其对人民币实际汇率的应用[J].经济学（季刊）,2003，(4).

[2]Kilic.R Linearity Tests and Stationarity[J].Econometrics Journal,2004，(7).

[3]Sandberg R.Critical Values for Linearity Tests in Time-varying smooth Transition Autoregressive Models When Data are Highly Persistent[J].Econometrics Journal,2008，(11).

[4]Kapetanios G,Shin Y C,Snell A．Testing for a Unit root in the Nonlinear STAR Framework[J].Journal of Econometrics,2003，112.

[5]Kilic R.Testing for a unit root in a stationary ESTAR process[J].Econometric Reviews,2011，(3).

[6]赵春艳.平滑转换自回归模型中线性检验与单位根检验问题研究[J].数量经济技术经济研究,2010，(7).

[7]Harvey D I,Leybourne S J.Testing for time Series Linearity[J].Econometrics Journal,2007，(10).

[8]赵春艳.平滑转换自回归模型的平稳性问题研究[J].数量经济技术经济研究,2012，(1)..

[9]Van Dijk D,Teräsvirta T.Smooth Transition Autoregressive Model--a Survey of Recent Developments[J].Econometrics Institute Research Report,2000，(23/A).