挖掘几何意义 巧解平面向量数量积问题

孔繁晶

(江苏省徐州高等师范学校 221116)

平面向量是高中数学课程的重要组成部分，具有集数形为一身的特征.同时又有着广泛的学科内及跨学科的应用价值.向量的数量积运算具有明显的几何意义，并且是类比、迁移等数学常用思维方法的良好载体，亦是历年各地高考命题的重点内容之一.

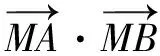
分析本题考查向量数量积问题，但用基底法和坐标法似乎都不易解答.但通过几何意义的分析，我们会有不一样的发现.

反思过程中最关键的解题步骤就是第一步，利用该结论是突破此问题的关键.该结论被称为极化恒等式.追溯其身世，出自高等数学泛函分析的内积空间.

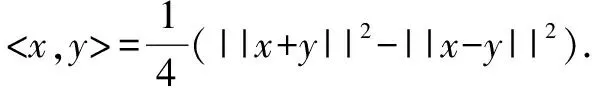
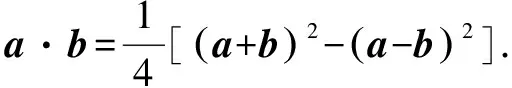
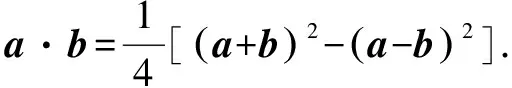
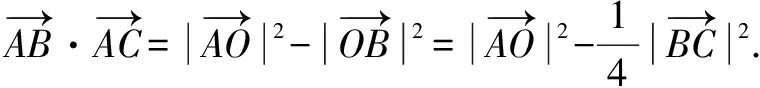
接着，我们来谈一谈利用极化恒等式巧解平面向量的数量积问题.

一、利用极化恒等式求向量的数量积

求解向量数量积是考查向量运算的常见题型，常规思路为利用定义法、坐标法、线性表示法.但有时以上条件不具备时，需要我们另辟蹊径，解决问题.

例1如图2，在ABCD中，已知则则的值为____.

练习1 如图3，在ABCD中，O为BD的中点，且OA=3，OC=5．若则的值是____．

小结解决共起点或是可以转化成共起点的两向量的数量积问题，可以借助极化恒等式转化为长度条件，再利用平面几何中平行四边形或是三角形的相关知识加以求解.

二、利用极化恒等式求向量数量积的最值或范围

向量数量积运算作为重要考点，还会结合函数、不等式考查其最值或取值范围的问题.

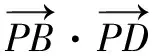
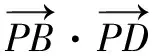
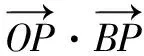
小结解决此类求数量积最值或是范围问题，常常先利用极化恒等式转化为长度条件，再利用平面几何知识找到临界位置进而确定最值或是范围.