立体几何求直线距离的三种解析方法
曹 静
(江苏省南通市第二中学高中校区 226000)
一、法向量在立体几何求直线距离中的使用
在求解立体几何题目时常构造法向量,可以将虚拟的空间距离通过坐标系进行具体化处理,实现解题过程由抽象向具体转化,实现解题过程的简单化,从而提升学生解立体几何题目的效率,保证解题结果的准确性.
例1如图1所示,a,b为异面曲线,E,F为异面曲线上的任意两点,n为a,b公垂线的方向向量,已知四边形ABCD是正方形,PD与面ABCD垂直,PD=AB=1,E,F分别是PB,PD中点,求直线AE与CF之间的距离.
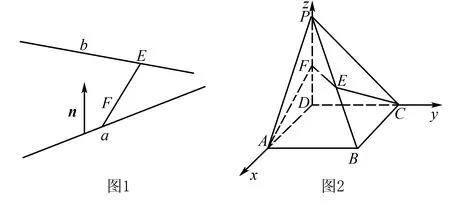
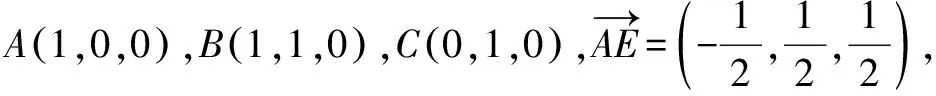

可见利用法向量求解距离问题时,可以简化解题过程,从而使得距离求解的结果更加准确,因此,教师们需要落实法向量在立体几何方面的教学.
二、等体积法在立体几何的运用
在求解某些异面直线的距离问题时,我们可以利用体积的不变性,从不同角度先将体积用不同的方式进行表达,从而建立方程进行求解.建立VA-A′C′D和VC-AA′D的体积的等量关系,再对等式进行化简,解出对应的异面直线的距离.
例2 如图3所示,若正方体ABCD-A′B′C′D′的棱长为1,求直线DA′与AC的距离.

解析因为直线AC∥平面A′C′D,且DA′⊂平面A′CD,所以直线AC与平面A′C′D之间的距离即为DA′与AC的距离.
设点A′到平面A′C′D的距离为d,连接A′C,DC,
由VA-A′C′D=VC-AA′D,
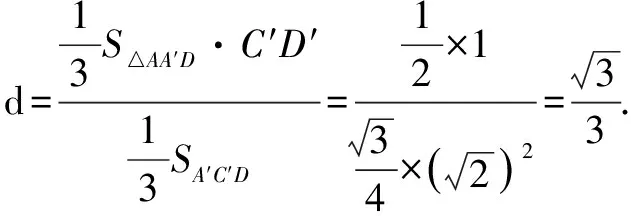

三、函数思想在立体几何中的应用
函数思想在立体几何中的应用即利用函数构建模式可以将立体几何问题进行简化处理.通过对题目的简化,能够使得同学们更容易且更好地理解题目的意思,从而帮助同学们更好地解题,把握题目考查的真实意思,从而节省思考的时间,提升同学们在该方面的解题质量.
例3如图4所示,AB为圆O直径,PA垂直于圆所在的平面,C为圆周上任意一点,设∠BAC=θ,PA=AB=2r,求PB与AC之间的距离.

分析通过读题可知,例3是求空间中的异面距离,也就是空间立体几何的问题,无法通过构建空间直角坐标系的方式进行解题,从而没有办法采用法向量进行求解.因此,与例3相似的这一类题型就需要通过函数思想的应用进行有效解题.由图可以发现PB与AC之间的距离可以看作是直线PB上的点与直线AC之间的距离,因此可以通过构建函数的形式进行求解.
解析在PB上任取一点M,使得MD⊥AC,并相交于点D,得出MH⊥AB于点H,进而垂直于面ABC.
因此,可以得出函数关系式:
MD2=x2+[(2r-x)sinθ]2.
对函数进行化简,可得出最终结果.
通过例3的求解,可见异面求距离的问题可以看作是函数中求最大值和最小值的问题,所以,对于这一类题目可以将其转化为函数进行解答,从而帮助同学们在解题的过程中简化整体的解题步骤.
综上所述,在高中数学有关立体几何问题的解答中,往往有两种较为常见的解析方式,即利用法向量与构建函数.一般来说,法向量较为常见,但是在一些题目中,法向量的应用会使得解题过程变得更为复杂,所以,函数的应用就能够解决法向量的问题.所以,教师在教学时应向同学们落实两种解题方法的应用,促使同学们能够在考试时选择最为合适的解题方法.

