MP⁃WFRFT调制信号星座裂变参数特性研究

江 彬，杨宇晓，高 萍

（南京航空航天大学 航天学院，江苏 南京 210016）

0 引 言

射频隐蔽技术是近年来被提出的一种新的隐身技术[1]，主要通过对通信、雷达等主动辐射源的特征控制，以提高其安全性能。

变换域通信[2]是射频隐蔽可用的技术手段之一，加权分数阶傅里叶变换[3]（Weighted Fractional Fourier Transform，WFRFT）具有加密性能好、抗识别能力强等优点，如今在变换域通信领域中已成为很多学者[4⁃8]研究的热点。文献[9⁃10]首先将WFRFT应用到通信系统，提出了基于WFRFT的数字通信系统框架。文献[11]对比了多径信道条件下的WFRFT信号星座图特征，从几何模型角度分析了星座分裂的原理。文献[12]深入分析了4⁃WFRFT信号的时频域分量特征，将星座图分裂归于时域信号分量的叠加值。文献[13]将混沌基函数设计方法引入多参数加权傅里叶变换通信系统，提高了通信系统的隐蔽性能。文献[14⁃15]针对MP⁃WFRFT的裂变模型，提出了应用于隐蔽通信的MP⁃WFRFT星座预编码设计方法。

综上所述，国内外学者针对多参数加权傅里叶变换开展了广泛而深入的研究，形成了丰富的研究成果，但相关研究还存在以下不足，具体体现在：针对星座裂变的基本原理研究较多，但对制约裂变特性的关键参数研究较少；针对特定信号特征的关键参数变换规律和取值范围研究仍有不足。

因此，本文针对上述问题，首先完成了MP⁃WFRFT（Multiple Parameterms Weighted⁃type Fractional Fourier Transform）星座裂变原理的理论推导，在此基础上，深入分析了模值比例因子、变换阶数α等星座裂变关键参数的变换规律及其取值特性，进而利用Matlab计算平台实现了模值比例因子、变换阶数等关键参数的仿真实验，验证了加权分数阶傅里叶域调制的星座裂变特性。最后，采用仿真的优选参数，利用软件无线电平台实际生成了MP⁃WFRFT调制信号。软件无线电平台采用FPGA芯片ZYNQ⁃ZC7045和AD9361实现。

1 MP⁃WFRFT变换域通信原理

MP⁃WFRFT变换域方法在加权分数阶傅里叶域内对信号的调制特征进行处理，使其信号特征发生改变，截获方在传统时频域内难以实现信号的逆变换处理，从而提高了信号的安全性能。4⁃WFRFT是研究较多的加权分数阶傅里叶变换域方法，本文以4⁃WFRFT为基础开展研究。

若X0为任意复数 序列，X1，X2和X3分 别是X0的0~3次离散傅里叶变换。则4⁃WFRFT定义如下：

式中：ωl为加权系数，l=0,1,2,3，ωl是α和V的函数，其定义为：

式中：α为变换阶数；V=[MV,NV]为尺度向量；mk，nk为MV=[m0,m1,m2,…,mM-1]和NV=[n0,n1,n2,…,nM-1]中的第k个元素，M为加权项数，在4⁃WFRFT系统中M=4。

为便于分析，将离散傅里叶变换表示为矩阵形式：

式中：N为序列X0的长度；λN=exp(-i2πN)。

因此，可将式（1）改写为矩阵相乘形式：

推广可得，X0的1~4次4⁃WFRFT变换S4W为：

式中，S0，S1，S2，S3分别为X0的1~4次4⁃WFRFT变换，且分别为S0的0~3次DFT，则：

由旋转相加性可得，W4W(α,V)W4W(-α,V)=I，则4⁃WFRFT的逆变换为：

2 星座裂变特性分析

星座图是衡量通信信号调制特性的重要工具，4⁃WFRFT可以使原有通信信号调制特征发生扩散、旋转和裂变等变化，从而显著改变信号的调制特征，提高通信信号的安全性能。本节通过理论推导，分析了4⁃WFRFT系统裂变的数学原理，并对加权模值间比值、α参数取值边界等裂变关键参数进行了分析和仿真。

2.1 星座裂变数学原理

鉴于F为DFT变换，由傅里叶变换的相关性质可得：

结合公式（4）可得，X2=F2X0，其中，相应分裂特性的产生是对应时域分量项的叠加，X0和X2表示时域部分也就决定了星座分裂的特性。因此，可将其组合并定义为星座裂变函数，如式（9）所示：

为便于分析，本节以QPSK信号为例，开展信号星座图裂变的机理分析。QPSK信号为四相调制体制，QPSK信号映射的X0和X2分布如表1所示。

表1 序列分布

令w0=a+bi，w2=c+di，将表1中的值分别代入到式（9）中得到表2。

表2 星座裂变分裂点

由表1和表2结果可知，在复平面上将表1中X所映射的4个点序列加权求和后，最多得到表2中分裂的16个点。因此，分裂点数可记为N2（N为原始信号的进制数）。

2.2 模值比例因子特性分析

4⁃WFRFT调制产生的星座分裂可显著改变原有信号的调制特征，在信号伪装等应用场景中，需要使调制后信号尽可能趋近于伪装信号，因此，还需要对4⁃WFRFT的分裂特性进行精确设计。X0和X2对应的基带星座点在复平面上相对固定，而不同参数[α,v]会产生不同的加权系数w0(α,v)和w2(α,v)，从而使裂变函数式产生不同的星座合成点，以改变星座图特征，提升系统的安全性能。

加权系数矢量w0(α,v)和w2(α,v)直接影响星座图裂变后的聚集点分布，其模值比例因子为星座图裂变的关键约束参数，本文令。

对于多参数4⁃WFRFT信号，将M=4代入到式（2）得：

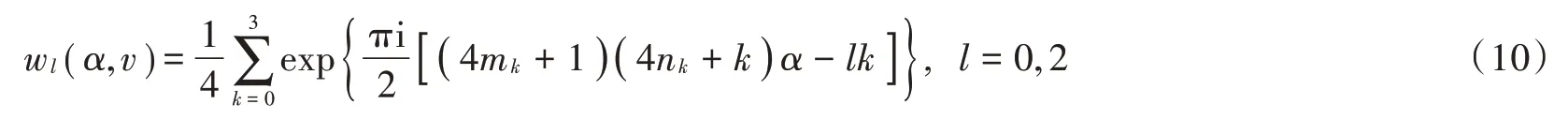
利用式（11）的欧拉公式，对式（10）进行变换，可得简化公式（12）：

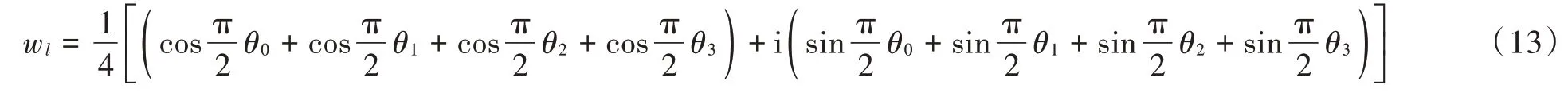
则式（13）模值为：

令：

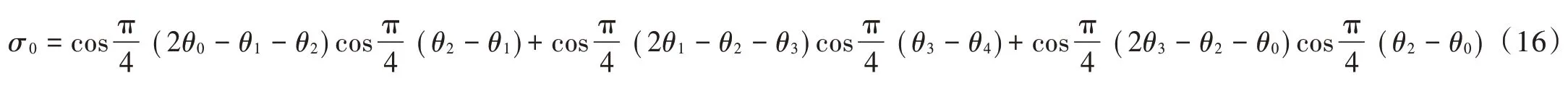
可得：

综上可知，在单一周期内：

此时η所推导的取值范围是一个避免X0和X2在被加权之后发生过度旋转和延伸不足的参考取值区间，而当模值比例因子取值为η端点值0.5或2时，调制信号的星座图聚集点为均匀分布。

2.3 变换阶数α阈值

由1.1节可知，4⁃WFRFT的变换阶数α以4为周期，α通常可取[2，-2]或[0，4]内实数，由式（4）可知，加权系数wl(α,v)是变换阶数α的函数，wl(α,v)随α变换呈现出旋转特性，从而影响星座图的裂变效果。因此，需深入分析变换阶数α的取值特性。

为便于分析，在α取值范围内分别选取10-1，10-2，10-3，10-4不同数量级取值，由式（12）可得：

令τ为α的取值极限，当τ=10-4时，。代入式（13），可得：

由上式可得：w0=1,w2=0。

此时，调制信号星座图裂变所产生的聚集点将出现重合，从而导致星座图分裂特性消失，无法实现星座图调制特征变化的效果。因此，在尺度向量常规取值条件下，α取值应大于10-4数量级。

3 仿真结果与分析

为验证本文对WFRFT关键参数研究的正确性，本节以QPSK信号为原始信号，以16QAM信号为调制目标，进行4⁃WFRFT变换域调制，并对关键参数进行仿真分析。

仿真1：模值比例因子仿真

本节针对模值比例因子关键参数，仿真计算了η取值范围内的不同取值，以比较η对调制信号星座图分裂特征的影响。若调制数据序列长度为1 024，变换阶数为α，尺度向量MV=[m0,m1,m2,m3]和NV=[n0,n1,n2,n3]取值如表3所示，则4⁃WFRFT调制后的星座图如图1所示。

表3 星座裂变参数

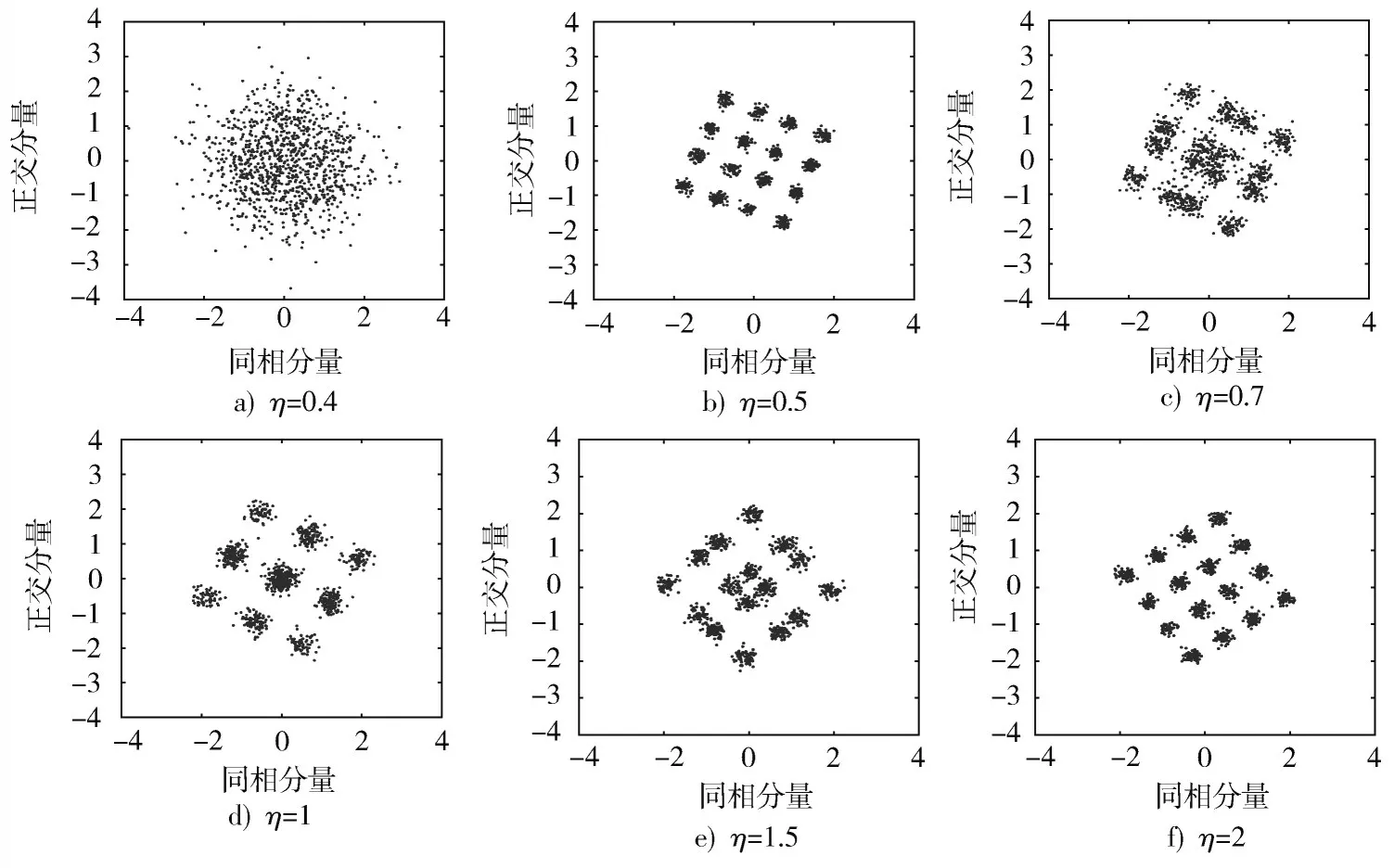
图1 η不同取值下的星座图分裂效果仿真

由仿真结果可知，通过改变η取值，可调整调制信号星座图聚合点间的分布特征。当η不在[0.5,2]内时调制信号星座图表现为类噪声特性；当η=1时，调制信号星座图中间区域的聚合点出现重合；当η取[0.5,2]以外其他值时，星座图聚合点呈现非均匀分布特征，当η取值为0.5或2时，星座图聚合点呈现均匀分布特征。

仿真2：α的阈值

为研究变换阶数α对星座图分裂特征的影响，本节将尺度向量MV=[m0,m1,m2,m3]和NV=[n0,n1,n2,n3]取值固定，仿真计算α在不同量级取值条件下的星座图裂变特征。若调制数据序列长度为1 024，MV=[1 1 1 1]，NV=[1 0 0 2]，α分布取值为0.1，0.01，0.001，0.000 1，则不同取值下的星座图裂变特征如图2所示。

图2 α不同取值下的星座图裂变效果仿真

由上述星座裂变特性仿真可知，随着α取值减小，星座图裂变后的聚合点由稀疏逐渐变化为聚集。其中当α等于10-1和10-2时，由图2a）和图2b）可见分裂的16个点；当α等于10-3时，由图2c）直观地观察到每4个点为一组并聚集成点簇；而当α等于10-4时，图2d）完全将16个点重合成了4个点。

4 软件无线电平台测试与验证

4.1 硬件平台的设计与搭建

本节采用第3节Matlab仿真获得的优选参数，利用软件无线电平台产生实际的4⁃WFRFT射频信号。软件无线电平台采用ZYNQ⁃7000系列FPGA，射频芯片选用AD9361。AD9361通过FMC接口与FPGA板连接，如图3所示。

图3 硬件实物图

4.2 参数设置

QPSK调制和4⁃WFRFT调制在FPGA中实现，调制后的基带数据分为I，Q两路传递至AD9361芯片，由AD9361实现调制数据的正交上变频。本节根据第3节仿真结果，确定参数α=0.06，MV=[3 6 0 0]，NV=[0 2 0 5]，此时，星座图的分裂特性较好。其他参数设置为：待调数据码速率为2 Mb/s，发射频点为2 422 MHz，采样率为40 MHz。频谱仪设置参数为：Span设为5 MHz，调制类型可为QPSK或16QAM。

4.3 实验验证

实验1：原始QPSK信号生成

本实验在FPGA中对待调数据进行QPSK映射调制，将调制后数据分为I，Q两路信号，经成型滤波后送入AD9361生成QPSK射频信号。图4为频谱仪接收的AD9361输出射频信号，由星座图可知，信号符合QPSK调制特征。

图4 原始QPSK信号图

实验2：4⁃WFRFT调制信号生成

本实验在实验1的基础上，在QPSK映射后增加了4⁃WFRFT调制模块，按照4.2节参数设置，图5为频谱仪接收的AD9361输出射频信号，由星座图可知，QPSK信号的调制特征发生了裂变，产生了16个聚合点。因此，通过4⁃WFRFT调制，将QPSK信号的调制特征改变为16QAM调制特征。

图5 多参4⁃WFRFT调制后频谱仪接收图

5 结 语

本文从理论上推导和分析了星座图裂变原理，将比例因子、变换阶数确定为星座图裂变的关键参数量，通过仿真计算，获得了比例因子的取值范围、变换阶数的取值下限，并利用Matlab平台仿真计算了目标调制为16QAM时的优选参数。最后，采用ZYNQ⁃ZC7045+AD9361软件无线电平台分别生成了原始QPSK信号和4⁃WFRFT信号，验证了4⁃WFRFT调制的星座图裂变特性。