对等结构下多节点INS误差修正
李寅龙,张天舒,刘 傲
(海军航空大学,山东 烟台 264001)
0 引 言
传统的多传感器跟踪系统一般采用集中式与分布式结构,集中式结构中各节点发送数据到融合中心进行信息处理,对融合中心的计算量、通信量都提出较高要求。分布式结构中每个节点都能独立处理局部观测数据,汇总到融合中心完成全局态势的信息融合[1⁃3]。但在态势瞬变的现代电子战中,多传感器与信号源传递数据造成信息爆炸,若我方遭遇电磁干扰导致融合中心瘫痪,此时依靠融合中心的集中式与分布式结构将失去作战能力,遭遇毁灭性打击。在此基础上提出对等式结构,其灵感来源于区块链和Ad⁃Hoc网络,实际上是一种分布式、去中心化的通信模式[4⁃5],不仅解决了集中式与分布式结构抗毁性差的问题,而且提高了成员之间的协同合作性。
惯性导航系统(INS)利用陀螺仪和加速度计进行自主式导航,不依赖外界信息并且能够提供全姿态信息,连续性好且噪声低,因此被广泛利用[6]。
但INS由于依靠积分算法提供姿态信息,容易产生累积误差,且误差与时间成正比。因此针对单个节点而言,INS无法长时间应用,现在广泛利用GPS等算法对INS误差进行弥补,但是当GPS无法使用时,INS难以进行精确定位[7]。利用对等式结构节点间可通信协作的优势对INS产生的累积误差进行修正,保证INS长时间运行的可靠性和有效性。
针对多节点INS误差修正的问题,文献[8]提出基于格网框架的GPS/SINS组合导航系统。文献[9]建立编队成员相对导航非线性运动模型,采用量测重构技术构造伪线性观测矩阵及协方差矩阵,提出了多平台INS误差联合修正算法。文献[10]利用GPS/INS数据更新节点位置与速度,通过四元数将方向线性化,利用EKF处理数据以达到更高的精度。文献[11]提出一种INS/数据链相结合的动态相对定位算法,利用最小二乘法对相对位置进行估计,提出秩亏网平差算法对定位误差进行校正。文献[12]提出通过杠杆臂校正传感器测量值,利用EKF、EMLog、深度传感器、陀螺仪对惯导系统进行集成。文献[13]针对GPS在遮挡情况下容易失灵和INS易偏离的问题,构建距离测量方程,提出相对测距的EKF团队协同定位算法。文献[14]建立INS/GPS运动模型,将次优衰落因子嵌入到预测协方差中,利用UKF修正系统误差,增强算法的鲁棒性。
上述文献将GPS与INS相结合建立运动模型,利用EKF或UKF提高定位精度,但存在以下缺点:若遭遇电磁静默、信号干扰等情况,GPS系统可能失灵;EKF需计算非线性函数的雅可比矩阵,计算量较高;UKF算法会出现中心采样点权值为负、协方差矩阵非正定的情况,降低定位精度与鲁棒性。
而本文在此基础上提出CKF误差修正算法,建立高精度节点非线性高斯运动模型,利用逼近系统后验均值与协方差的等权值采样点进行滤波,利用对等结构节点间可协同合作的通信优势,修正全局节点的INS误差,计算量小、收敛速度快且稳定性高,具有很强的鲁棒性。
1 模型建立
对等式结构采用时分多址(TDMA)的通信方式且标定精确统一的入网时间,每个节点有固定的报告顺序,依次循环发言完成整个周期,最终掌握全局态势。如图1所示,每个节点具有同等的通信地位,节点间相互通信联结成巨大的信息池,可以有选择地从中获取所需的信息。
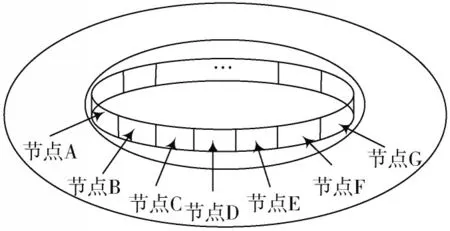
图1 信息池示意图
假设在对等式结构中存在多个节点,其中,节点A导航精度最高,建立节点A在某一时间段的非线性高斯运动模型,利用CKF滤波器优化节点A的导航信息,其余待修正节点在信息池中获取节点A的导航信息得到精确的节点间相对距离,将各自INS解算的相对距离与之相减作为量测值,建立误差修正模型,对INS误差参数进行开环输出校正。
2 算法原理
2.1 坐标系转换
为了统一全局态势,全局节点将采用地心直角坐标系进行信息交换,将直角坐标系转换为地心直角坐标系的公式为:
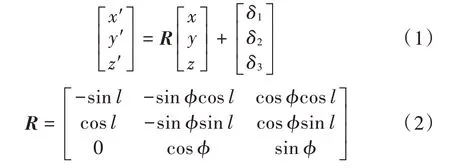
式中:(x′,y′,z′)为地心直角坐标系坐标;l为该点经度;φ为该点纬度;δ1,δ2,δ3为转换误差,本文为简化计算忽略不计。
2.2 CKF滤波
CKF利用三阶Spherical⁃Radial Cubature准则选择2n个等权值的Cubature点计算高斯权重积分,CKF的具体滤波过程如下[15]。
1)初始化
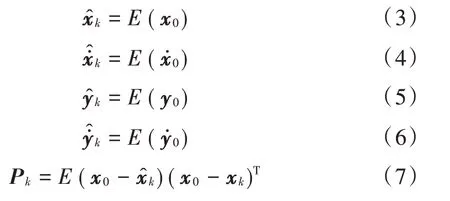
2)时间更新
利用Cholesky分解误差协方差矩阵Pk得到Sk:



3)量测值更新
计算用于量测值更新的Cubature点:


量测误差协方差矩阵为:

量测互相关协方差矩阵为:

滤波增益为:

状态矢量估计值为:
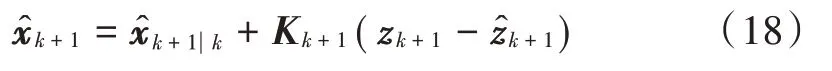
更新误差协方差矩阵为:
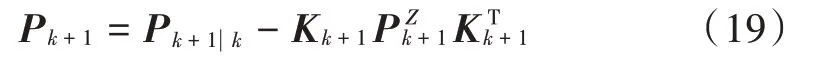
3 算法步骤
3.1 CKF滤波模型
建立节点A某时间段非线性高斯转弯运动模型观测方程如下:
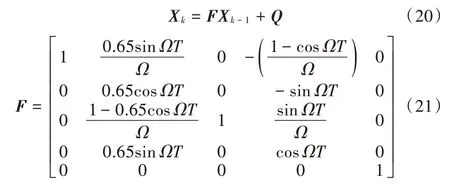

建立过程噪声矩阵为:式中:Q为服从高斯分布的非奇异协方差矩阵;q1,q2的值与过程噪声的强度有关。
建立节点A运动模型的CKF量测方程为:

3.2 INS误差修正模型
以CKF输出的xk,yk作为输入,建立惯导误差修正模型如下:
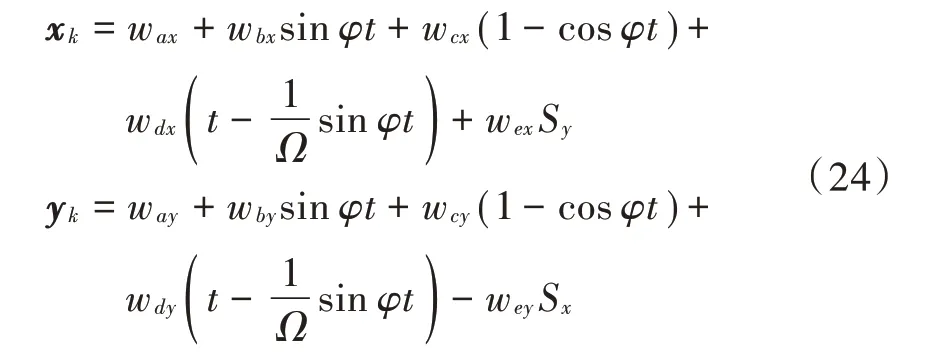
式中:wax,…,wex和way,…,wey为节点INS误差参数在x,y方向的分量,分别代表距离误差、速度误差、加速度计误差、陀螺仪误差、方位偏角误差;Sx,Sy代表在x,y方向的移动距离。
建立状态方程为:
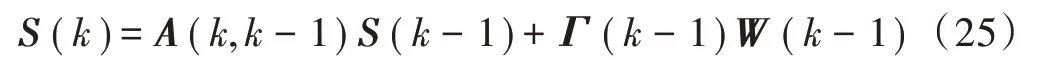
式中:S(k)=[wax wbx wcx wdx wex];A(k,k-1)的非零项为A3,3=1,A4,4=1,A5,5=1。
建立观测方程为:

式中γ为地球自转角速度。
设定各噪声矩阵,对INS误差参数进行开环输出校正。INS误差修正流程如图2所示。
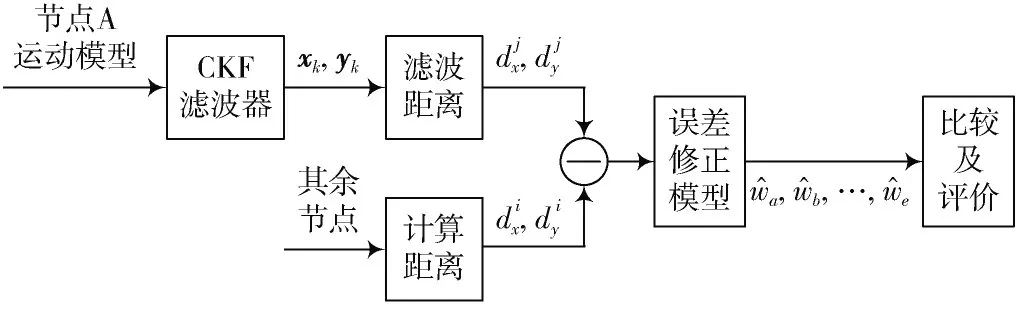
图2 INS误差修正流程
首先在对等结构中选择导航精度最高的节点A建立某时间段运动模型,利用CKF优化节点位置精度,其余节点从信息池中获取节点A位置矢量xk,yk,利用实测节点间相对距离与根据INS导航信息计算出的相对距离之差作为量测值建立误差修正模型。通过误差修正模型、卡尔曼滤波计算INS误差参数,…,,完成对INS误差参数的开环数据矫正。
4 仿真分析
4.1 仿真环境
假设导航精度最高的节点A某时间段做非线性转弯运动,初始位置为(1,1)km,初始速度为100 m/s,初始转弯率为-30(°)/s。其余节点初始运动速度随机在300~700 m/s之间,角度随机在0~2π之间。以节点B代表其余节点进行INS误差修正,设定节点B的INS误差参数为:距离误差wa=50 m,速度误差wb=10 m/s,加速度计初始误差wc=3×10-5g,随着时间增长到5×10-5g,并含有加速度计高斯随机零偏1×10-5g,陀螺仪误差wd=0.01(°)/h,随着时间增长到0.02(°)/h,并有高斯随机陀螺仪漂移误差0.01(°)/h,方位偏角误差we=0.5°。
4.2 仿真结果
如图3所示,对节点A在某时间段内x,y方向的位置及速度进行EKF及CKF滤波。仿真结果表明,在节点A做转弯运动时各分量的滤波值在10 s后逐渐稳定,CKF能以较快速度收敛,其稳定性优于EKF,且CKF取得较高的精度,具有很强的鲁棒性。

图3 位置及速度滤波结果对比图
x,y方向CKF滤波后的速度及位置误差示意图如图4,图5所示,总体误差在10 s后逐渐趋向于0,即滤波值等于真实值,并能够在10~100 s的时刻保持稳定滤波,表明CKF滤波具有很好的非线性近似能力。

图4 CKF在x方向位置、速度估计误差
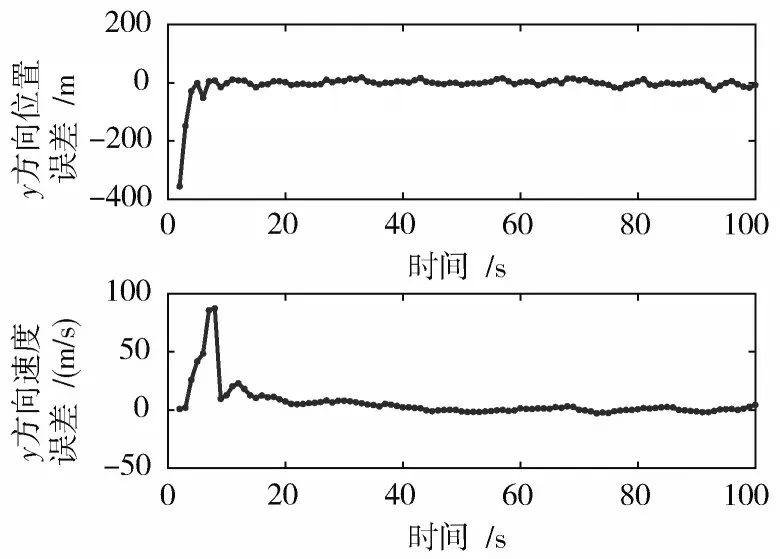
图5 CKF在y方向位置、速度估计误差
节点A运动模型转弯率的滤波值与真实值对比图如图6所示。由于采样初期容积点数据较少,滤波值尚不稳定,在10 s后滤波转弯率逐渐稳定,20 s后滤波转弯率接近真实转弯率,直至完全吻合,仿真结果验证CKF对转弯运动模型有较好的跟踪能力。

图6 转弯率滤波结果对比图
节点A运动轨迹的滤波结果与真实轨迹对比图如图7所示。仿真结果表明,CKF对于节点A的转弯运动模型具有很好的跟踪效果,滤波值接近真实值。

图7 运动轨迹滤波结果对比图
如图8,图9所示,其中:“○”曲线是节点A与节点B在x,y方向的相对距离真实值曲线;“*”曲线是节点B的未校正INS推算的相对距离曲线,由于INS误差参数中的加速度计误差和陀螺仪误差与时间成正比,因此“*”曲线增长的趋势越来越快;“△”曲线是利用本文算法校正后节点B利用INS解算出的相对距离曲线,仿真表明“△”曲线相比“*”曲线更接近真实值曲线,表明本文算法能够对INS误差进行有效的修正。
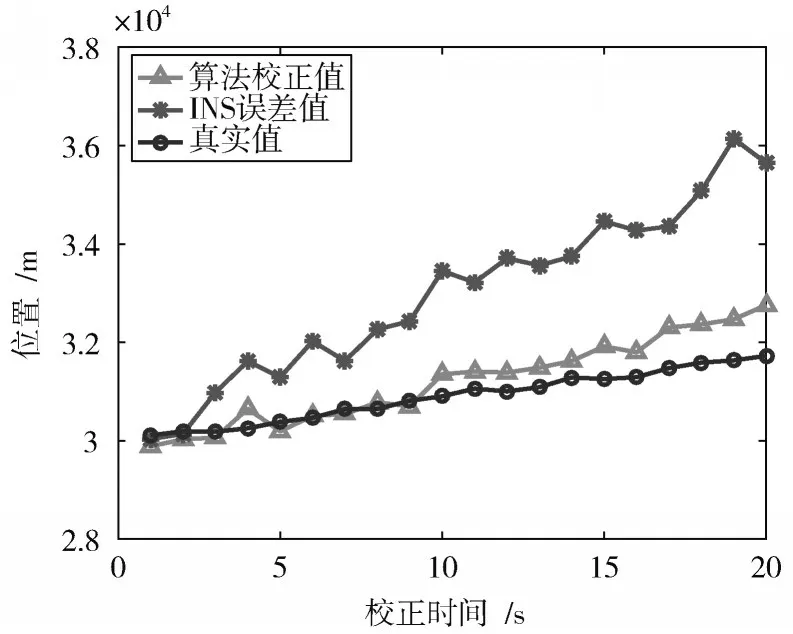
图8 x方向真实值与校正后误差曲线

图9 y方向真实值与校正后误差曲线
5 结 语
本文在传统多传感器跟踪分布式结构的基础上提出无中心化的对等式结构。针对INS系统误差随时间累积的问题,在对等结构下利用CKF对导航精度高的节点建模得到导航信息,通过误差修正模型对其余节点进行INS误差修正,仿真结果表明,CKF能够对非线性转弯运动有较好的跟踪效果,其稳定性与收敛速度皆优于EKF,且导航精度更高,具有较好的鲁棒性,能够对INS的系统误差进行有效修正。

