适用于非常模信号的常数模新算法
饶伟,孙辉, 郭业才, 邓承志, 汪胜前, 田伟
(1. 南昌工程学院 信息工程学院,江西 南昌 330099;
2. 南京信息工程大学 电子与信息工程学院,江苏 南京 210044)
1 引言
在现代数字传输系统中,自适应均衡器是接收机的一个非常重要的组成部分,它能有效地抵消由多径传输和有限信道带宽引起的码间干扰。与传统的自适应均衡相比,盲均衡不需要使用训练序列,能有效提高信道带宽利用率,其中由 Godard提出的常数模盲均衡算法[1](CMA, constant modulus algorithm)因其强鲁棒性和易于实现性,在数字传输系统中应用广泛[2]。
CMA通过梯度搜索法[1]不断更新均衡器抽头系数,以最小化代价函数,其目的是使均衡器输出信号的幅度模值都等于一个固定的统计模值。CMA不但适用于信源字符占据同一个幅度模值的常模信号(如8-PSK),而且还适用于信源字符占据多个幅度模值的非常模信号(如16-QAM)[2],如图1所示。在一些理想环境中,对于常模信号CMA可以实现理想(迫零)均衡,但是对于非常模信号CMA稳态均方误差(MSE, mean square error)无法至零[2,3]。
徐金标等[4]提出了停止与前进的 SAG-CMA,当均衡器输出数据可靠时,用信源的多幅度模值代替统计模值对抽头系数进行迭代更新,降低 CMA稳态MSE,但是这样一种方式使大量可用于抽头系数迭代的数据被排除,致使算法收敛速度比 CMA慢;文献[5]对Sign-CMA进行了改进,当接收信号落入判决域内时,使用多模CMA对非常模信号进行均衡,从而减小稳态MSE,提高收敛速度,但是其判决域是通过手动设置的经验值来确定的。文献[6,7]对不同的 QAM 信号使用匹配的模值进行均衡,提升了均衡效果,但是算法却受到某些参数或条件的限制。文献[8,9]利用坐标变换将16-QAM变换成了4-QAM常模信号,从而减小了稳态MSE。文献[10]提出了一种修正多模CMA,称为MCMA,该算法将 CMA代价函数分为实部和虚部两个部分,用2个统计模值对接收信号进行均衡,该算法性能优于传统CMA[10,11]。可见,使非常模信号的幅度模值与统计模值相匹配是降低算法稳态MSE的有效途径,但上述方法都需要借助辅助的参数或条件,且算法稳态MSE的大小均没有提供理论证明。
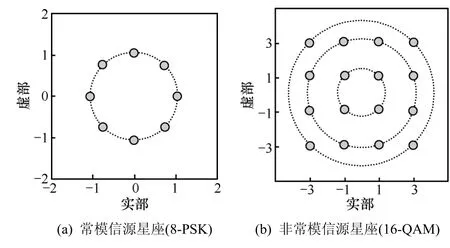
图1 常模信号与非常模信号星库图
本文通过研究4-PAM和16-QAM非常模信源星座的特点,定义了一种幅度模值变换方式,可将非常模信源的多个幅度模值变换成单一幅度模值。将该变换方式应用于CMA代价函数中,得到适用于上述两种非常模信号的新 CMA,新算法的目的是使均衡器的输出信号幅度模值经过相同的变换方式后,其新幅度模值与统计模值相等,从而减小了稳态MSE,并且减少均衡器误操作从而提高了收敛速度。理论证明和仿真实验均表明新算法在无噪声环境下,其稳态MSE近似为零;在实际有噪水声信道中,新算法同样具有比CMA更优的均衡性能。
2 CMA
CMA2-2是CMA中的特例[2],具有良好的收敛性能,因此本文只讨论CMA2-2,为表示方便,将CMA2-2简称为CMA。CMA基带等效模型如图2所示。
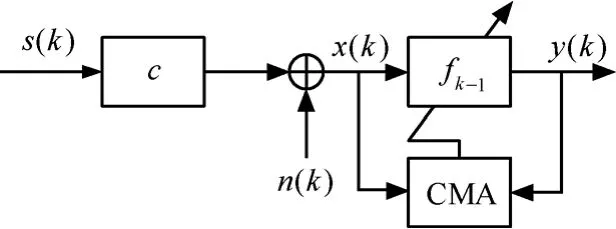
图2 CMA基带等效模型
其中,s(k)是信源序列;c是信道的冲激响应;n(k)是信道高斯白噪声序列; x(k)是均衡器的输入序列; fk-1是均衡器抽头系数向量且长度为N; y(k)是均衡器的输出序列。
令x= [ x(k ) ,x(k-1 ),…,x(k-N+1)]T, f =kk-1,“T”表示转置,则均衡器的输出为

CMA的代价函数定义为
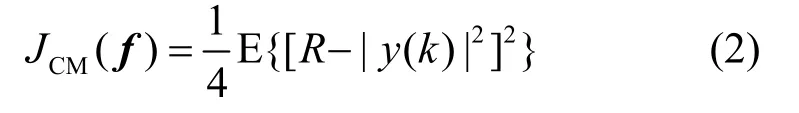
式中,R为信源的统计模值,定义为

可见,R由信源的幅度模值|s(k ) |决定。
利用瞬时梯度下降法对f进行更新,以最小化代价函数,则更新公式为
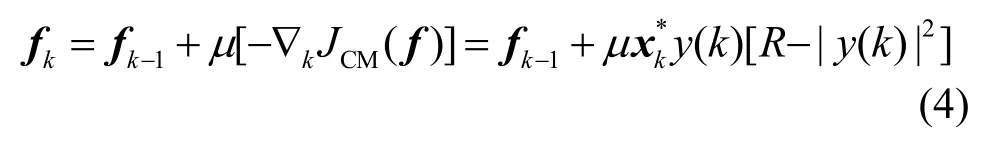
式中,∇kJCM(f )表示对代价函数求瞬时梯度,μ为步长,*表示复数共轭操作,且定义 eo(k )= y(k)为CMA误差函数项。
由代价函数式(2)可知,CMA的目的是期望每个输出信号的幅度模值的平方能与R相等或此时代价函数被最小化为零,均衡器抽头系数稳定。对于常模信源,如8-PSK,其星座坐标为则|s(k)|= 1 ;又根据式(3)得 R = 1 ,因此当均衡器输出信号满足成立,均衡器实现了理想均衡,且代价函数为零,均衡器抽头系数稳定。但是对于非常模信源,如16-QAM,其星座坐标为s(k) = {±1 ±j,±3 ±j,±1 ±3 j,±3 ±3 j},其对应3个不同的幅度模值:;又根据式(3)得,所以即使均衡器输出信号与信源完全重合(理想均衡),也无法满足,此时对应的CMA代价函数值并不为零,致使均衡器抽头系数一直保持(不为零的)微幅调整状态,从而改变了原本理想的均衡器输出。因此,CMA非常适合用于常模信号,而对于非常模信号CMA虽然能够完成均衡,但稳态误差大,收敛速度慢。
3 基于幅度模值变换的CMA
通过上述分析可知,对于非常模信号,信源的多幅度模值与 CMA统计模值不匹配是造成 CMA性能下降的主要原因之一。因此本文针对4-PAM和16-QAM 2种非常模信号,定义了一种幅度模值变换方法,可将多幅度模值变换成单一幅度模值,并将其应用于CMA代价函数中,从而提升CMA对非常模信号的均衡性能。
为分析简便,先考虑4-PAM非常模实信号,其信源星座坐标为,对应的幅度模值为,统计模值为,此时。定义信源幅度模值变换方式
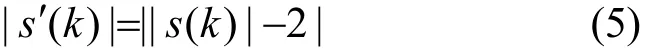
式中,|s′(k)|为信源新模值,将|s(k)|= { 1,3}带入上式得|s′(k)|=1,且信源新模值对应的新统计模值R′为
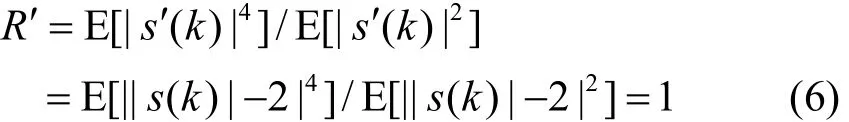
可见,利用式(5)可以将4-PAM非常模实信源的多幅度模值|s(k)|= { 1,3},变换成单一幅度模值|s′(k)|=1,并且
因此定义CMA新代价函数
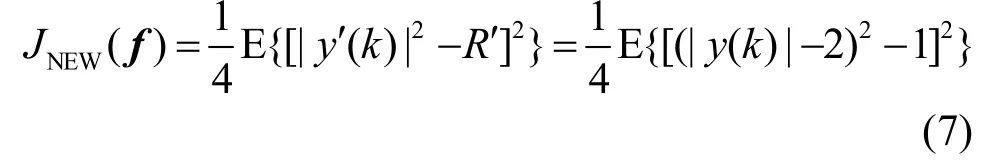
均衡器抽头系数更新公式为

将基于新代价函数式(7)和均衡器抽头系数更新式(8)的新常数模算法记为 MT-CMA(Modulus Transformation-based CMA),且定义式(8)中为MT-CMA误差函数项。MT-CMA的目的是使均衡器输出信号的幅度模值经过变换后,其新幅度模值与新统计模值相等。当 MT-CMA理想均衡时,有代入式(7)得JNEW(f )= 0,代入式(8)得 fk=fk-1。
文献[10]提出了一种修正的 CMA,称为MCMA,该算法将CMA代价函数分为实部和虚部两个部分,该算法性能优于传统 CMA[10,11]。考虑到如果将 4-PAM信源坐标 s(k)={±1,±3}进行虚部扩展:{±1,±3} +j{±1,±3},则变成16-QAM信源坐标 s (k) = {±1 ±j,±3 ±j,±1 ±3 j,±3 ±3 j}。因此利用MCMA中的实部和虚部分开的方法得到适用于16-QAM非常模复信号的MT-CMA:
1) 代价函数定义为
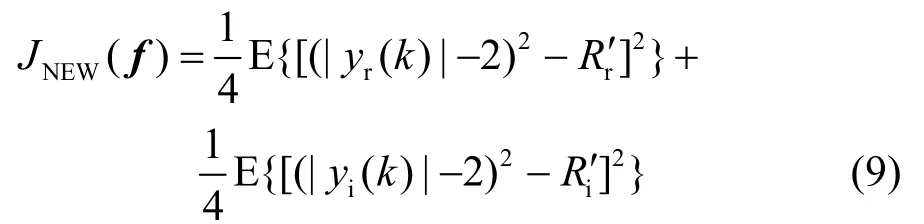
式中, yr(k)、 yi(k)分别为输出信号的实部、虚部,Rr′、 Ri′分别定义为

式中, sr(k)、 si(k)分别为信源的实部、虚部。
2) 均衡器抽头系数更新公式为

4 稳态MSE性能分析
Mai和Sayed在无信道噪声的环境下,提出了一种反馈式性能评估方法[3],能够较为精确地对均衡器的稳态MSE进行评估[12,13]。因此本文也采用该方法,在信源信号分别为 4-PAM 实信号和16-QAM复信时,对MT-CMA的稳态MSE进行评估。
考虑权向量迭代公式

用迫零均衡器抽头系数向量 fZF同时减上式两边得
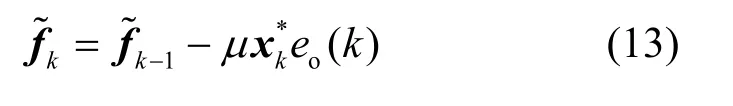
式中, f˜k=fZF-fk。定义先验和后验误差分别为
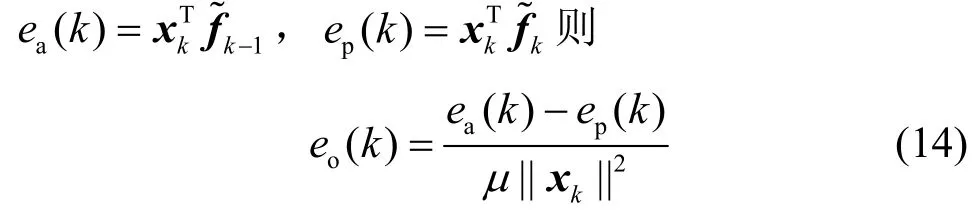
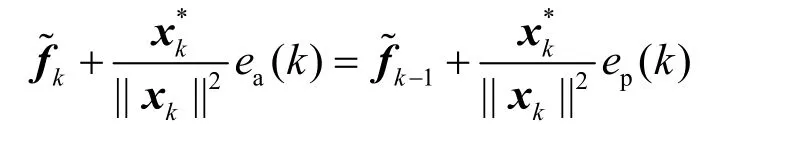
对等式两边取模的平方并求期望得
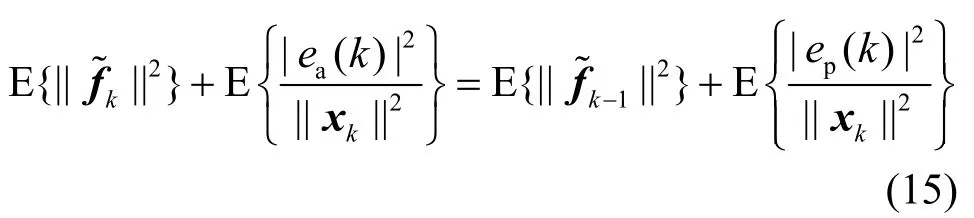
这里并不讨论算法是否能够收敛,只讨论算法收敛后的均方误差,所以有下式成立
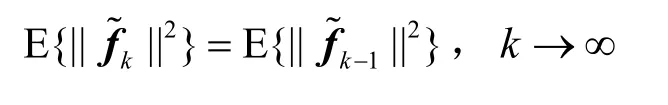
代入式(15)得
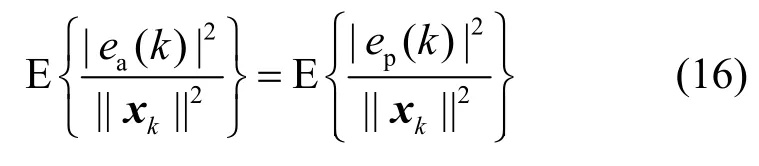
结合式(14)得
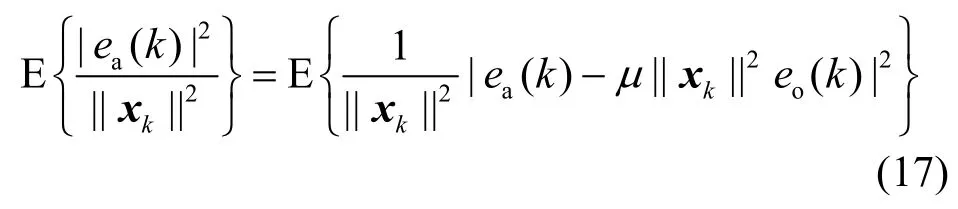
为表示方便,省略式中的k,并展开等式右边得
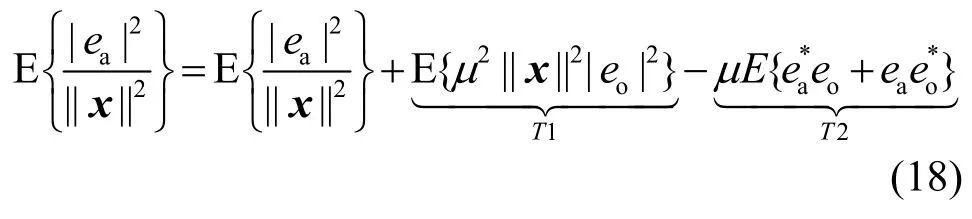
可见,式中T1和T2相等。通过该等式,可以得到算法的稳态MSE:E[|ea|2]。
对于MT-CMA的稳态MSE分析是建立在文献[3]中的合理假设之上:s与 ea相互独立,与y相互独立。此外,在分析中假设μ足够小,并且稳态时 | ea|2也足够小。
4.1 信源信号为4-PAM时
1) 计算T1


因为μ和 ea2足够小,因此可以忽略包含有μ2和 ea的2次或更高次幂项[3],此外s与 ea相互独立,故
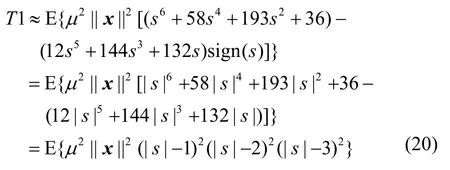
2) 计算T2
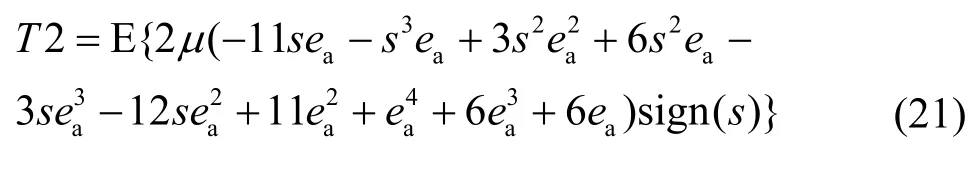
因为s与 ea相互独立,并且当μ和 ea2足够小时可以忽略包含有 μ ea4项[3],所以
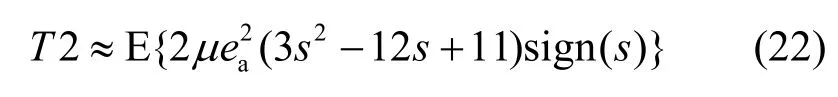
令T1= T2,得到MT-CMA的稳态MSE
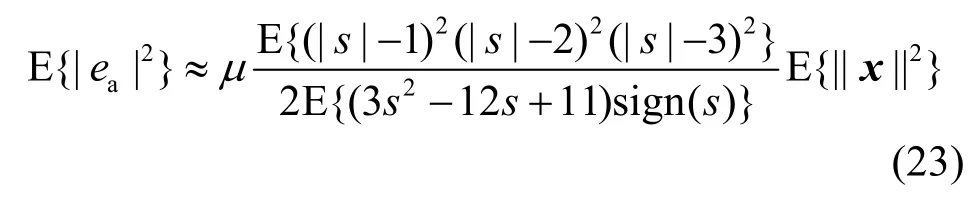
对于4-PAM,由于其信源坐标为 s ={±1,±3},即有,所以此时MT-CMA的稳态误差为

而CMA在对非常模实信号进行均衡时的稳态MSE为[3]
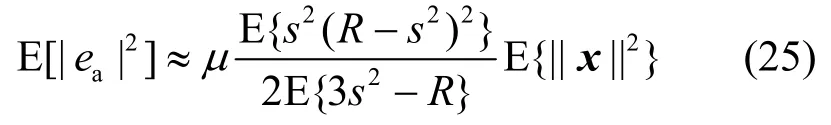
因为对于 4-PAM 信源有 R ≠|s|2,所以此时CMA稳态MSE,
显然,对于4-PAM非常模实信号,在无信道噪声情况下MT-CMA的稳态MSE远小于CMA。
4.2 信源信号为16-QAM时
同理,对于16-QAM复信号可得MT-CMA的稳态MSE

由于 16-QAM其信源坐标为 s ={±1 ±j,±3 ± j,±1 ±3 j,±3 ±3 j},即有sr={±1,±3}以及si={±1,±3},从而有以及所以此时MT-CMA的稳态误差为

而CMA在对非常模复信号进行均衡时的稳态MSE为[3]
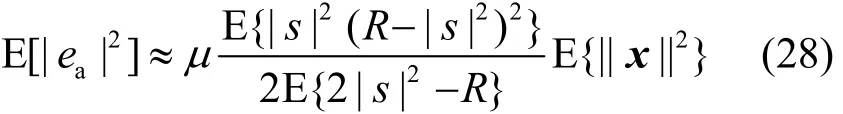
对于16-QAM 信源有 R ≠|s|2,所以此时CMA稳态MSE, E
显然,对于16-QAM非常模实信号,在无信道噪声情况下 MT-CMA的稳态 MSE同样远小于CMA。
5 计算机仿真分析
5.1 无噪声实信道环境仿真实验
利用计算机仿真,来验证上述理论分析的正确性。仿真实信道的冲激响应为 c =[-0.0901,0.6853,0.7170,0.0901][3],无信道噪声;信源为4-PAM;CMA和MT-CMA均采用T/2分数间隔均衡器结构[2],均衡器抽头个数均为 4,步长分别为 0.000 06和0.000 8。仿真结果如图3所示,当两算法收敛后,MT-CMA输出稳态 MSE约为-300dB,即MSE ≈ 1 0-30近似为0,远远小于CMA稳态MSE;且MT-CMA收敛速度比CMA快。

图3 4-PAM仿真学习曲线图
5.2 有噪声水声信道环境仿真实验
为了进一步检验 MT-CMA的有效性,采用文献[14]中的浅海水声信道模型进行仿真实验,该模型已经通过了海上实验具有很高的精度。信道模型参数为:海深20m,风速为每小时20海里,声速为1 500m/s,载波频率为10kHz,信道带宽为2kHz,声源和接收点布放深度均为10m且相距5 000m,信息传输率为4k字符/s,选用声压幅度较大的10条本征声线,声线参数如表1所示。信道的脉冲响应由式(26)计算[15]
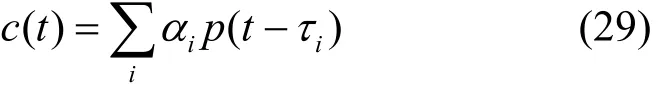
式中,αi为声压幅度,τi为相对延时,p(t)为滚降系数为20%的升余弦脉冲。计算求得信道冲激响应为 c =[0.5850 - 0 .5671 - 1 .0000 -0.3571 0.2608 0.1605- 0 .1336 - 0 .0874]。
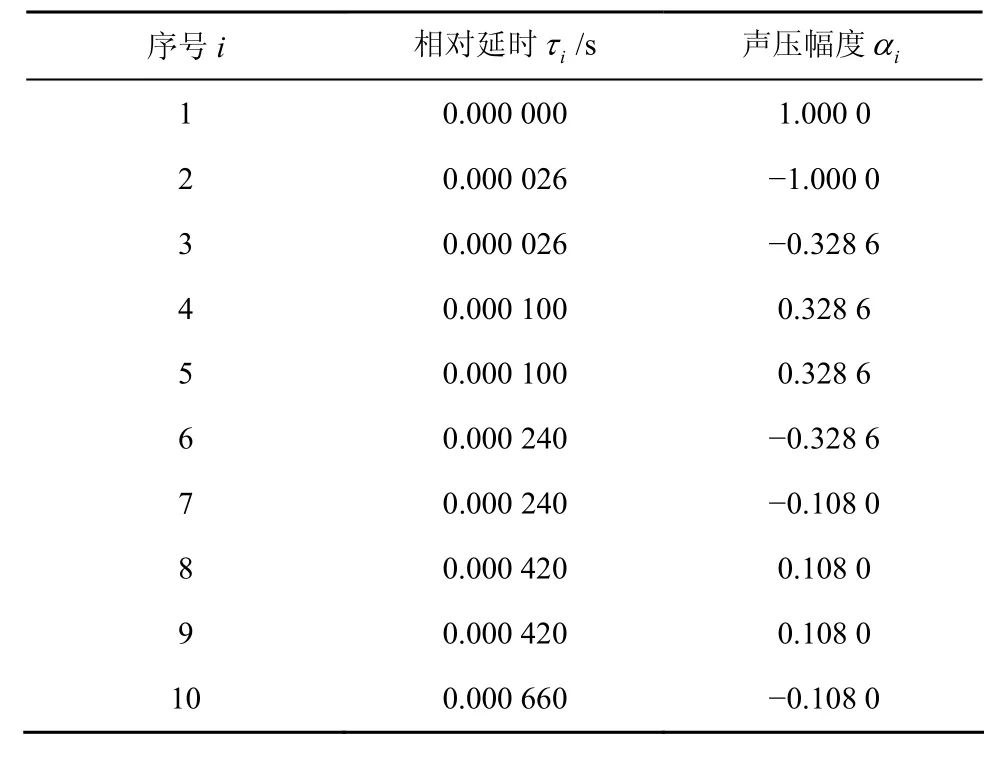
表1 信道本征声线参数
信源为 16-QAM 且能量归一化,信噪比为18dB;由于在复信源情况下 MT-CMA借助了MCMA实、虚部分开处理的方法,因此将MT-CMA与CMA和MCMA进行对比,三者均采用T/2分数间隔均衡器结构,均衡器抽头个数均为 4,其步长分别为 0.03、0.004、0.06。各均衡器的 MSE曲线如图4所示,MT-CMA稳态MSE最小约-19.5dB,比CMA、MCMA分别小了约4.5dB、4dB。图5~图7分别是各均衡器的输出星座图,MT-CMA输出星座比其他均衡器输出星座更加清晰。

图4 不同信噪比下算法稳态MSE

图5 CMA输出星座
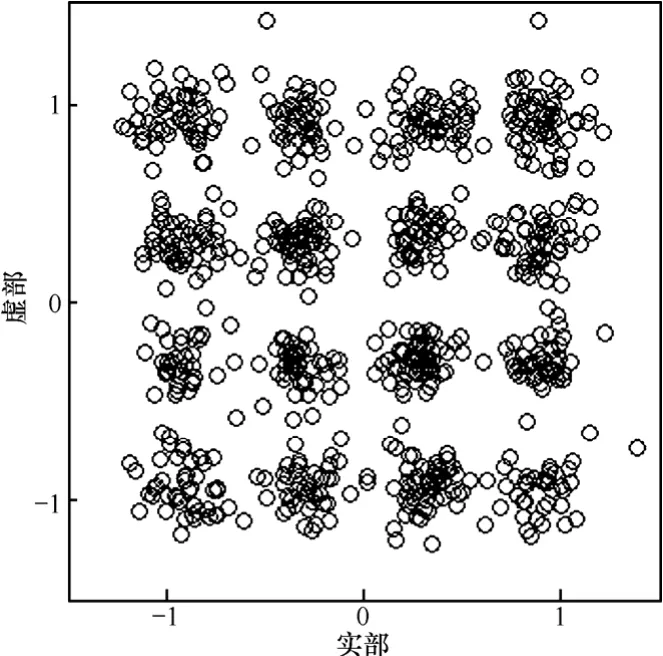
图6 MCMA输出星座
6 结束语
非常模信号的多幅度模值与CMA统计模值不匹配,是CMA在对非常模信号进行均衡时,稳态MSE无法收敛至零的主要原因之一。本文定义的新代价函数能将4-PAM和16-QAM这2种非常模信号的多个幅度模值变换成单一幅度模值,从而使算法的稳态MSE收敛至零。理论证明和仿真实验均表明,新算法均衡效果较其他类似算法有显著的提高。
[1] GODARD D. Self-recovering equalization and carrier tracking in two dimensional data communication systems [J]. IEEE Transactions on Communications, 1980, 28(11): 1867-1875.
[2] JOHNSON C R, SCHNITER J P. Blind equalization using the constant modulus criterion: a review[J]. Proceedings of the IEEE, 1998, 86(10):1927-1950.
[3] MAI J, SAYED A H. A feedback approach to the steady-state performance of fractionally spaced blind adaptive equalizers[J]. IEEE Transactions on Signal Processing, 2000, 48(1): 80-91.
[4] 徐金标,葛建华. 一种新的盲均衡算法[J]. 通信学报, 1995, 16(5):78-81.XU J B, GE J H. A new blind equalization algorithm[J]. Journal of China Institute of Communications, 1995, 16(5): 78-81.
[5] 郑应强, 李平, 张振仁. 用于MQAM调制的双模式Sign-CMA盲均衡算法[J]. 通信学报, 2004, 25(5): 155-159.ZHENG Y Q, LI P, ZHANG Z R. Dual-mode blind equalization algorithm for multi-level QAM modulation based on Sign-CMA [J]. Journal on Communications, 2004, 25(5): 155-159.
[6] BARBAROSSA S, SCAGLIONE A. Blind equalization using cost function matched to signal constellation[A]. Proceedings of the 31th Asilomar Conference on Signals, Systems and Computers[C]. USA:IEEE Comput Soc, 1997. 550-554.
[7] GUO Y C, RAO W. A new dual-mode algorithm for multi-modulus blind equalization suitable for higher-order QAM signals[A]. Processings of the First International Symposium on Test Automation and Instrumentation[C]. Beijing: World Publishing Corporation, 2006.529-533.
[8] RAO W, YUAN K M. A simple constant modulus algorithm for blind equalization suitable for 16-QAM signal[A]. 9th International Conference on Signal Processing[C]. USA: Institute of Electrical and Electronics Engineers Inc., 2008. 1963-1966.
[9] GUO Y, ZHAO X. A modified T/2 fractionally spaced coordinate transformation blind equalization algorithm [J]. Int J Communications,Network and System Sciences, 2010, 3(2): 183-189.
[10] OH K N, CHIN Y O. New blind equalization techniques based on constant modulus algorithm[A]. IEEE Global Telecommunications Conference[C]. GLOBECOM '95, 1995, 2: 865-869.
[11] LIN J C, LEE L S. A modified blind equalization technique based on a constant modulus algorithm[A]. IEEE International Conference on Communications[C]. ICC 98, 1998, 1: 344-348.
[12] THAIUPATHUMP T, HE L, KASSAM S A. Square contour algorithm for blind equalization of QAM signals[J]. Signal Processing, 2006,86(11): 3357-3370.
[13] MAGNO T, SILVA M, VITOR H. Nascimento. Improving the tracking capability of adaptive filters via convex combination[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 3137-3149.
[14] ZIELINSKI A, YOON Y H, WU L X. Performance analysis of digital acoustic communication in a shallow water channel[J]. IEEE Journal of Oceanic Engineering, 1995, 20(4): 293-299.
[15] TONG L. Blind sequence estimation[J]. IEEE Trans Communication,1995, 43(12): 2986 -2994.

