基于Piecewise直方图均衡化的图像增强方法

陈文飞，廖斌，许雪峰，黄志勇，董文永

（1. 武汉大学 计算机学院，湖北 武汉 430072；

2. 湖北大学 数学与计算机科学学院，湖北 武汉 430062；

3．成都东软信息技术职业学院 计算机科学与技术系，四川 成都 611844）

1 引言

图像增强是低级图像处理中最重要的问题之一。直方图均衡化是一种增强图像对比度的标准技术[1]，其目的是为了改善低对比度图像的质量，以便于图像和视频等内容的后期处理。直方图均衡化的基本思想是通过对输入图像的亮度值的概率尽可能进行均匀分布，以扩展图像的动态显示范围和增强图像对比度。由于缺乏通用的统一理论和有效的图像质量的评价标准，所以图像增强任务非常复杂[2]。

到目前为止，基于直方图的图像增强方法主要包括以下 3 类：全局方法[3～10]、局部方法[11～15]和混合方法[16,17]。全局方法或是利用图像全局直方图的多个波峰段分别进行均衡化[3]，或是利用平均亮度或等面积对直方图分段均衡化[4～9]，或是利用图像非线性映射因子对直方图进行转换后再累积分布进行均衡化[10]。但是，这种方法在对比度比较大的情况下有时不能获得好的处理结果。局部方法或将图像分块或分层后进行均衡化处理[11～14]，或在均衡化时利用图像的局部特征（例如局部均值、标准差或边缘）来修改局部直方图[15]（例如局部直方图均衡化、局部直方图拉伸和非线性映射等）。局部方法最大局限是亮度饱和和边缘效应等问题，因此为了解决局部方法这一问题，出现了大量平滑局部直方图的方法[18～21]。例如Yoon等[21]提出了基于固定大小的滑动窗口在整幅图像上移动，在滑动窗口内利用均值对直方图进行平滑，以达到图像增强的目的，但是需要手工调整参数。混合方法则结合上述2种方法的特点，同时使用全局直方图和图像的局部信息（例如梯度或边缘）达到改善图像的目的。朱立新等[17]对图像梯度场进行直方图均衡化，使图像阴影或高亮区域中的细节能够在梯度域内得到增强，但是有时图像会失真。

鉴于直方图均衡化方法本身的离散化特点[1]，现有直方图均衡化方法不可避免地存在不同程度的灰度“吞噬”现象，特别是当原始图像的质量比较差、灰度动态范围小和直方图分布极不均匀时，变换后图像的灰度范围一般很难达到图像格式所允许的最大灰度变化范围，图像的层次感表现得不好。因此，对一幅图像进行传统的直方图均衡化处理的过程就是一个熵减小的过程，这表明丢失了原图像某些信息。

本文针对上述“吞噬”现象和亮度饱和等问题，提出了一种 Piecewise 直方图均衡化方法以保证图像在直方图均衡化处理后保持熵不变。同时，结合了图像亮度全局拉伸和直方图均衡化2种方法的优点，使得图像具有自然和谐的视觉效果。

2 直方图均衡化性质

传统的直方图对图像亮度值进行排序，描述的是图像中该灰度级别的像素个数。在归一化之后，该离散函数可以看成是图像中具有相同灰度值的像素出现的概率密度函数。直方图均衡化的过程就是重新分配像素的亮度值，使得图像直方图中所有亮度分布尽可能扩展。

假设输入图像被归一化，那么直方图均衡化的过程[1]描述如下：

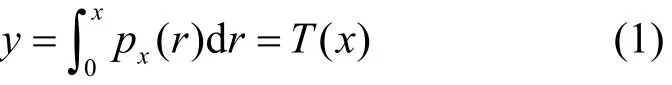
其中，y表示结果图像的亮度，x表示输入图像的亮度，r表示积分变量， px(r)表示输入图像的亮度的密度分布函数，T表示直方图均衡化函数。x和y的范围位于[0,1]之间。

直方图均衡化在增强对比度低的图像时简单而有效，尤其在只包含单一物体或背景和前景物体没有明显对比度变化时。但是当上述条件不满足时，该方法存在亮度增强不足或饱和的问题。尽管自适应直方图或局部直方图均衡化在一定程度上可以解决该问题，但是仍然有上述缺陷，而且也无法保证图像信息的熵不变性。归根到底，原图像在直方图均衡化处理后丢失了一部分原图的信息，丢失的信息一般是数量很少的像素[1,16,22]，这种现象本文称之为“吞噬”现象（如图1所示）。

图1(a)的直方图像素值为 r0的bin因均衡化在图1(b)中被 s1、 s2、 s3吞噬。

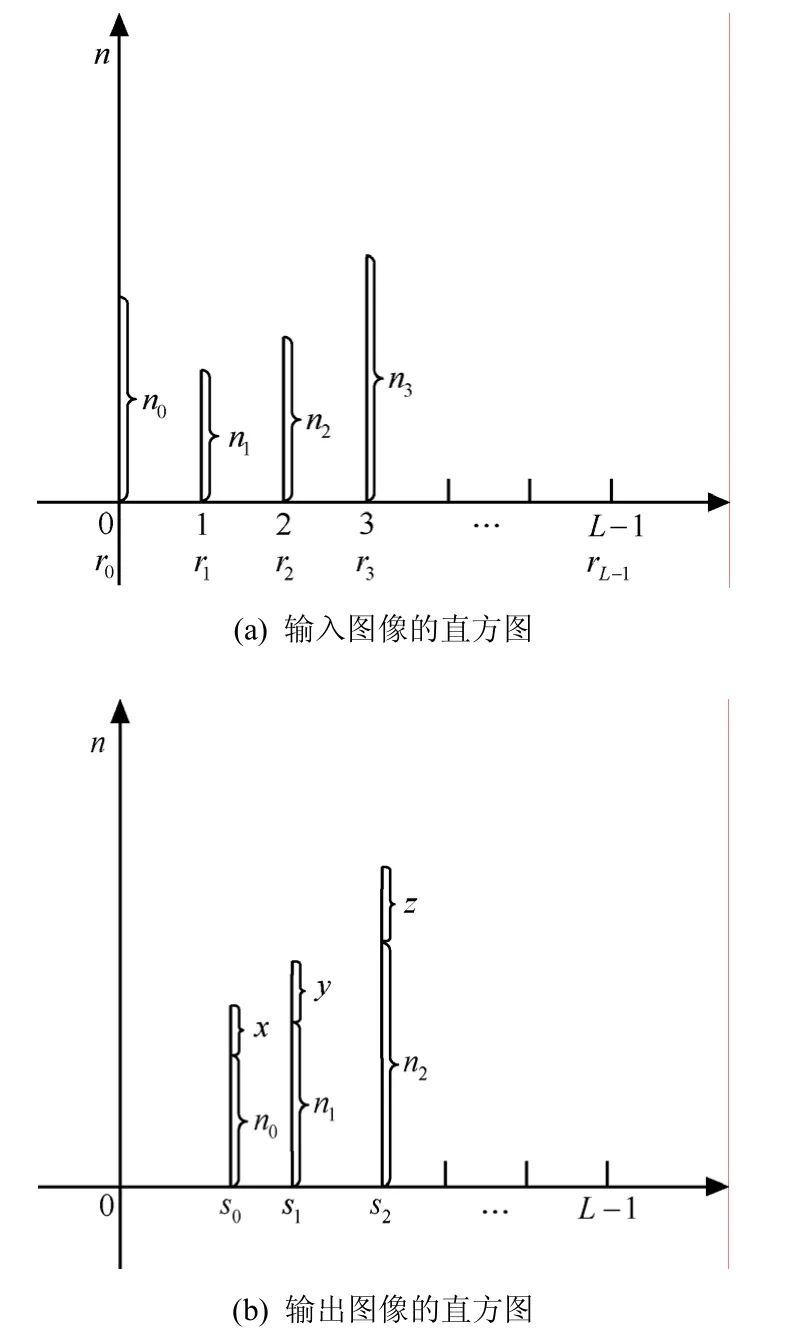
图1 “吞噬”现象

定理 1 当直方图均衡化时如果相关（不一定相邻）的灰度级发生了“吞噬”，则图像的信息量（即熵值）是减少的。

证明 假设原图像I直方图中相邻的灰度级 rk和 rk+1出现的概率分别为 prk和 prk+1。

这里灰度级 rk的熵为 e(rk)= - prklog prk，灰度级 rk+1的熵为 e (rk+1) = - prk+1log(prk+1)。

则原图像的熵值为

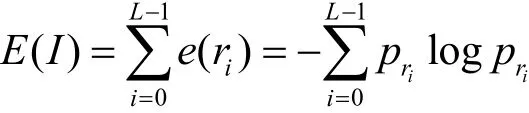
不失一般性，假设当直方图均衡化时，相邻的灰度级 rk和 rk+1之间发生了“吞噬”，并且在增强后图像J的灰度级s发生了“合并”。I的总像素个数。在直方图均衡化后，增强后图像J

反证法。假设 e (rk)+e (rk+1)≤e (s)，则与结论矛盾。

因此假设不成立。故当直方图均衡化时如果相关（不一定相邻）的灰度级发生了“吞噬”，则E(I) ＞ E(J)。证毕。

根据定理 1，在进行直方图均衡化时，只要发生了“吞噬”现象熵值必然减小。这也正是提出在直方图均衡化的过程中尽量避免“吞噬”的原因。

3 Piecewise直方图均衡化

3.1 理论基础

因为直方图均衡化只能改变原图像中同一灰度层上所有像素的灰度，却不能改变单个像素点在直方图上的分布。从信息的角度来看，原图中同一灰度层上的像素点代表了相同的信息，不能通过变换使原本带有相同信息的像素点变成带有不同信息的像素点。因此造成了在对灰度呈现两端分布或者在低灰度区域有较多像素点的图像进行直方图均衡处理后，得不到满意的效果，常常表现为处理后图像的亮度过度提升或细节消失，而整幅图像的灰度动态范围没有有效提升，达不到突出图像细节的目的。

定义 对于一幅具有L灰度级的图像I而言，通过直方图均衡化变换后得到输出图像J。如果在I上灰度级 rk的像素点个数 H (rk)非零，那么在J中对应的灰度级 sk与相邻的灰度级 sk-1之间的距离Δsk定义为

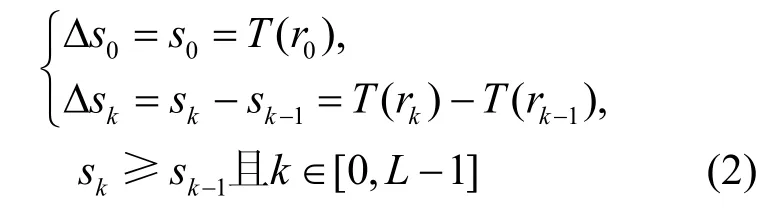
这里 sk表示均衡化后的灰度级，T表示直方图均衡化变换，L表示最大的灰度级。

由式(2)可知：当0 ＜ Δsk＜ 1 时，则输入图像I中的灰度级 rk表示的像素点在输出图像J中被灰度级T(rk)吞噬。

本文的目的是为了防止输入图像I在直方图均衡化变换后，造成输出图像J中发生灰度级“吞噬”或相邻灰度级之间的距离过大等问题。所以在直方图均衡化变换的基础上，引入了一个新的变换T′(s)：

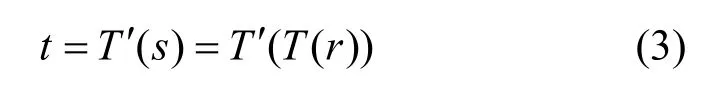
其中，t表示结果图像的灰度级，s表示中间结果的灰度级，r表示输入图像的灰度级。

这里要求T变换满足：T(r)在区间0≤r≤1中为单值且单调递增（严格）；当0≤r≤1时，0 ≤ T(r )≤1[1]。同时要求T′变换满足：T′(s)在区间0≤s≤1中为单值且单调递增（严格）；当0≤s≤1时，0≤ T′ (s)≤1；当H(r)≠ 0 ，Δsk≥1,k∈ ［0, L-1］。

为此定义T′变换如下，令 t0= s0= T (r0)：

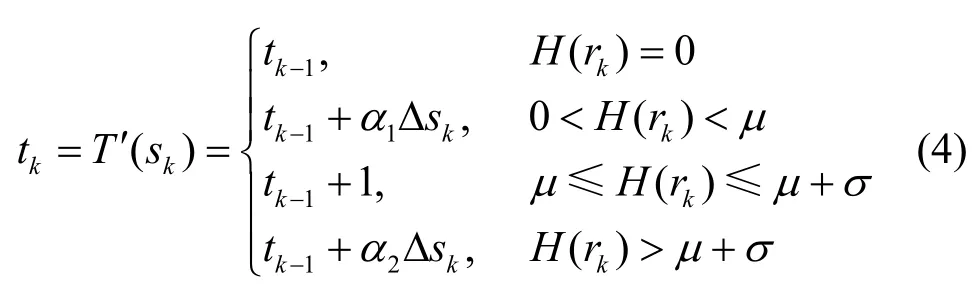
其中，t表示结果图像的灰度级，s表示中间结果的灰度级，H表示输入图像的直方图，T表示直方图均衡化变换，α1和α2表示距离控制参数。

μ和σ分别表示输入图像的直方图的均值和标准差，定义如下：

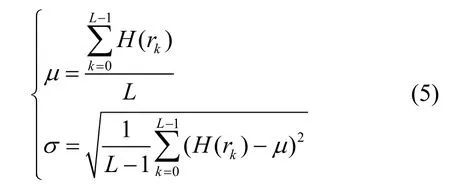
式(4)中的未知数α1和α2容易求解，假设0 ＜ H(rk) ＜μ的灰度级个数为λ1，μ≤H(rk)≤μ+σ的灰度级个数为λ2，H(rk)＞μ+σ的灰度级个数为λ3。根据式(4)，可以得到距离控制公式：

这里 Di( H(rk) )表示不同情况下直方图中 Bin的距离之和，α1和α2是距离控制参数。

所以可以得到：

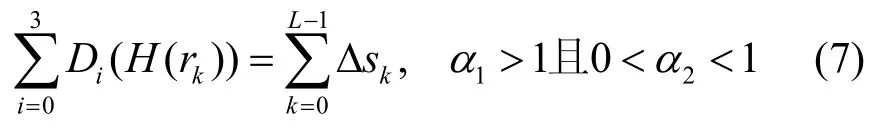
为了保证式(6)中当0 ＜H (rk) ＜ μ 时，∀α1Δsk≥ 1，由此可以得到：

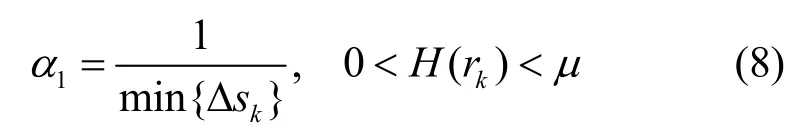
结合式(6)～式(8)，易得α2。

定理2 在原图像I直方图中如果∀r,s.t.HI(r ) ≠0 ,在映射 s=f(r)后增强图像J直方图中对应的灰度级s满足 HJ(s)=HI(r)关系，那么在相关的灰度级之间不存在“吞噬”。这里对映射 f的要求是其定义域和值域为[0,255]，且单调递增。

证明 反证法。假设相关的灰度级之间存在“吞噬”，根据定理1可知，则图像的信息量（即熵值）是减少的。

已知原图像I和增强图像J的总像素个数N不变，并且在原图像中假设存在一个灰度级r， HI(r) ≠0 ，则其熵值为

∵ HJ(s)=HI(r)∴e(s)= e(r)

因为在原图像I中任意一个 HI(r) ≠0 的灰度级r，都可以在映射f后的增强图像J中找到一个且仅一个灰度级s，并且两者的熵值相等。

所以 E (I)=E (J)，这与假设矛盾。

故定理2成立，证毕。

通过定理 2，可以推论出在直方图均衡化过程中发生“吞噬”现象的必要条件。但是这个条件在处理过程中很少满足，因此在处理中尽量保持熵值不变这一条件。

3.2 参数选取

一般情况下，例如原图亮度分配平均或原图较暗时，可以同时保证α1＞1且0＜α2＜1。但是在特殊情况下，例如当整幅图像过亮时利用式(6)～式(8)计算可能出现α2＜0。所以不能简单地使用上式来计算α1和α2。

这时，假设当0 ＜ H(rk) ≤ μ +σ时灰度级的个数为 λ =λ1+λ2，则式(6)变形为

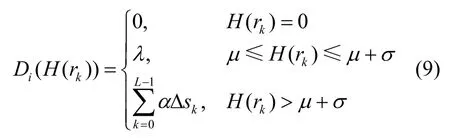
这里 Di( H(rk))表示不同情况下直方图中 Bin的距离之和，α是一个新的距离控制参数。

所以可以得到：

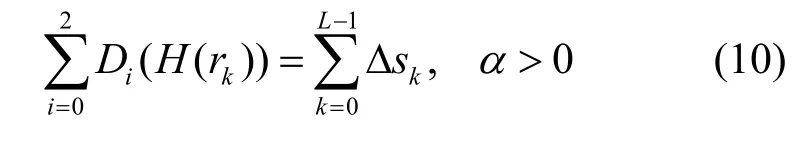
这里λ已知，根据式(9)和式(10)只需求解α即可。

同理，式(4)将变形为

定理 3 如果原图像I在直方图均衡化过程中满足式(4)或式(11)，那么增强图像J的熵值是不变的。

证明 根据式(4)可知α1＞1且0＜α2＜1，并且

假设当H(rk)≠ 0 时，tk= T′ (sk) =tk-1+a,a≥ 1 。

不失一般性，当 H (rk+1) ≠0 时， tk+1=T ′ (sk+1)= tk+ b=tk-1+ a+b ,b≥1。

易知 tk+1＞ tk。同理不论 H (rk-1)是否等于 0，tk＞tk-1。

所以可以得到当 H (rk) ≠0 时， tk= T ′(T(rk))是一一对应的，故 H (rk)=H (tk)。

根据定理2得到 E (J )=E (I)。

同理，在特殊情况下，当α1＞1且α2＜0时，根据式(11)易证 α Δsk≥ 1，满足定理2。证毕。

从定理3可以看出，在满足条件式(4)或式(11)的前提下。可以做到在直方图均衡化过程中满足熵值不变这一条件。

3.3 算法实现

1) 对于给定大小m×n的输入图像I，计算出该图像的直方图 H (r)；

2) 根据式(5)计算输入图像的直方图的均值μ与标准差σ；

3) 根据传统的直方图均衡化算法得到映射表s =T (r)；

4) 根据式(6)～式(8)计算距离控制参数α1和α2；

5) 判断α2的取值范围，如果大于0，则转到步骤7)；

6) 根据式(9)和式(10)计算新的距离控制参数α，转到步骤8)；

7) 根据式(4)计算新的映射关系t= T ′(s)，转到步骤9)；

8) 根据式(11)计算新的映射关系t= T ′(s)；

9) 根据上一步中的映射关系函数将输入图像I中所有像素灰度值映射到输出图像。

4 实验结果与分析

本文提出的保持熵不变的直方图均衡化算法是一种全局均衡化方法，处理结果具有自然和谐的视觉效果。

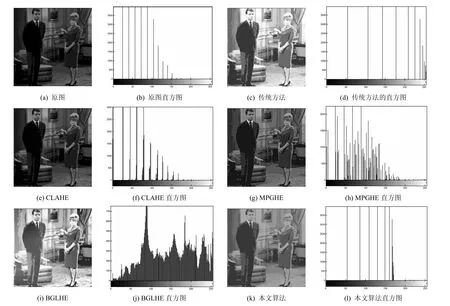
图2 灰度图的处理效果

图2 (a)是原图couple，一幅256×256的低灰度级的待增强图像，整幅图像偏暗，其原图直方图表明该图亮度较低且动态范围不大。图2(c)是采用传统直方图均衡化[1]处理后的结果，其直方图得到一定程度的拉伸，并且整体右移，造成图像亮度饱和现象。图2(e)是采用CLAHE算法[12]后的子块处理结果，直方图整体形状没有发生大的变化，图像与原图比较效果没有显著增加。图 2(g)是采用multi-peak GHE算法[15]处理后的结果，因为利用了梯度信息，所以其图像明显带有块效应，尤其是边缘部分效果欠佳。图2(i)是采用了使用bilateral grid的LHE算法[14]后的处理效果，空间采样率是100，范围采样率是 256，图像本身效果类似于传统直方图均衡化处理的效果，也存在严重的亮度饱和及块效应。图2(k)是本文的算法，图像显得自然柔和，均衡化处理后不存在亮度饱和等问题。

直方图均衡化在处理类似X射线和CT等高动态范围的医疗图像时，很难做到在均衡化的同时保留那些具有很小亮度范围的细节部分。图3(a)是原图skeleton，一幅1 024×842的低对比度的X射线医疗图像，整幅图像偏亮，其直方图表明整幅图像亮度偏亮，并且细节部分亮度接近。图3(c)是采用传统直方图均衡化[1]处理后的结果，其直方图得到一定程度的拉伸，但是图像中细节部分不清楚。图3(e)是采用 CLAHE算法[12]后的子块处理结果，直方图整体形状没有发生大的变化，直方图中概率值过大的部分都经过受限处理，可以清楚看到软组织、骨骼（包括胸椎）、纵隔、气管和支气、胸膜等组织。图3(g)是采用multi-peak GHE算法[15]处理后的结果，其图像明显带有处理后新出现的纹理，并且引入了新的噪声，影响了视觉效果。图 3(i)是采用了使用bilateral grid的LHE算法[14]后的处理效果，空间采样率是243.75，范围采样率是0.003 9，处理后图像本身效果类似于CLAHE效果。图3(k)是本文的算法，图像显得自然柔和，均衡化处理后不存在亮度饱和等问题。

为了将本文方法推广到彩色图像的处理，通过实验发现：为了保留图像的亮度和避免色调偏移，可以只将本文算法应用到图像的亮度部分。步骤如下：先将彩色图像转换到色彩成分相关性较低的Lab彩色空间，然后仅对亮度通道L进行直方图均衡化处理并保持a和b成分不变，最后通过反变换得到彩色图像。

图3 CT医疗图像的处理效果

图4 彩色图的处理效果

表1 各图像的熵

实验结果如下：图 4(a)是原图 monk，一幅 696×448的彩色图像，整幅图像色调偏暗。图4(b)是采用传统直方图均衡化[1]处理后的结果，整幅图像亮度饱和，影响了图像中的色调部分乃至纹理，造成图像中的细节部分不清楚。图4(c)是采用CLAHE算法[12]后的子块处理结果，保留了图像的大部分特征，但是亮度的增强影响了菩萨的纹理，不符合人眼的要求。图4(d)是采用multi-peak GHE算法[15]处理后的结果，其图像明显带有处理后新出现的纹理，并且引入了新的噪声，影响了视觉效果。图 4(e)是采用了使用bilateral grid的LHE算法[14]后的处理效果，空间和范围采样率采用缺省参数，处理后图像中廊柱边缘出现了黑边。图4(f)是本文算法，图像显得自然柔和，保留了原图像的特征，更加符合人眼要求。

为了避免直方图均衡化处理时发生亮度饱和及像素“吞噬”现象，本文方法在保持图像特征和熵不变的情况下，可以使得图像具有自然柔和的视觉效果。从表1可知：对于低对比度的灰度图图像而言，传统方法因为存在“吞噬”现象，熵值减小；而CLAHE/MPGHE/BGLHE的熵值都有所增加，这说明了这3种方法生成了概率分布更加均匀图像，但是这3种方法都使用了插值方法，方法复杂并且未必可以保证解决亮度饱和等问题，尤其是MPGHE使用了图像梯度信息，造成图像添加了新的边缘和噪声（这里。本文算法在灰度图中可以很好地保持图像的动态范围和熵不变下取得较好的视觉效果。在彩色图情况下，本文图像同样可以在尽量保持图像的熵不变（这里的熵值等于RGB3个平面的熵值之和）的情况下，取得自然的视觉效果。

5 结束语

本文针对直方图均衡化过程中像素“吞噬”和亮度饱和等现象，提出了一种新的图像对比度增强新算法。该算法是基于传统直方图均衡化的思想，提出了一种自动的距离控制方法以防止出现像素“吞噬”。实验证明本文算法在保留图像细节的同时，有效地克服了图像过亮或像素“吞噬”等现象，可以很好地保持原图像的特征和自然的视觉效果。为了提高该算法的通用性，后续的研究工作主要是：如何更好地利用图像的梯度或显著性等信息，使图像在对比度增强的同时，更好地凸显其特征。

[1] 冈萨雷斯 R C，伍兹 R E. 数字图像处理[M]. 北京: 电子工业出版社, 2003.GONZALEZ. R C，WOODS R E. Digital Image Processing[M].Beijing: Publishing House of Electronics Industry, 2003.

[2] PANETTA K A, WHARTON E J, AGAIAN S S. Human visual system-based image enhancement and logarithmic contrast measure[J].Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, 2008, 38(1): 174-188.

[3] WONGSRITONG K, KITTAYARUASIRIWAT K, CHEEVASUVIT F, et al. Contrast enhancement using multipeak histogram equalization with brightness preserving[A]. The 1998 IEEE Asia-Pacific Conference on Circuits and Systems[C]. Chiangmai, Thailomd, 1998. 455-458.

[4] OOI C H, KONG N S P, IBRAHIM H. Bi-histogram equalization with a plateau limit for digital image enhancement[J]. Consumer Electronics, IEEE Transactions on, 2009, 55(4): 2072-2080.

[5] SIM K S, TSO C P, TAN Y Y. Recursive sub-image histogram equalization applied to gray scale images[J]. Pattern Recognition Letters, 2007, 28(10): 1209-1221.

[6] CHEN S D, RAMLI A R. Minimum mean brightness error bi-histogram equalization in contrast enhancement[J]. Consumer Electronics, IEEE Transactions on, 2003, 49(4): 1310-1319.

[7] CHEN S D, RAMLI A R. Contrast enhancement using recursive mean-separate histogram equalization for scalable brightness preservation[J]. Consumer Electronics, IEEE Transactions on, 2003, 49(4):1301-1309.

[8] WANG Y, CHEN Q, ZHANG B. Image enhancement based on equal area dualistic sub-image histogram equalization method[J]. Consumer Electronics, IEEE Transactions on, 1999, 45(1): 68-75.

[9] KIM Y T. Contrast enhancement using brightness preserving bi-histogram equalization[J]. Consumer Electronics, IEEE Transactions on, 1997, 43(1): 1-8.

[10] HOSSAIN M F, ALSHARIF M R. Image enhancement based on logarithmic transform coefficient and adaptive histogram equalization[A]. 2007 International Conference on Convergence Information Technology[C]. Gyongju, Korea, 2007.1439-1444.

[11] PIZER S M, AMBURN E P, AUSTIN J D, et al. Adaptive histogram equalization and its variations[J]. Computer Vision, Graphics, and Image Processing, 1987, 39(3): 355-368.

[12] PISANO E D, ZONG S, HEMMINGER B M, et al. Contrast limited adaptive histogram equalization image processing to improve the detection of simulated spiculations in dense mammograms[J]. Journal of Digital Imaging, 1998, 11(4): 193-200.

[13] 江巨浪，张佑生，薛峰等. 保持图像亮度的局部直方图均衡算法[J].电子学报, 2006, 34(5): 861-866.JIANG J L, ZHANG Y S, XUE F, et al. Local histogram equalization with brightness preservation[J]. Acta Electronica Sinica, 2006, 34(5):861-866.

[14] CHEN J, PARIS S, DURAND F. Real-time edge-aware image processing with the bilateral grid[J]. ACM Transactions on Graphics(TOG), 2007, 26(3): 103.

[15] CHENG H D, SHI X J. A simple and effective histogram equalization approach to image enhancement[J]. Digital Signal Processing: a Review Journal, 2004, 14(2): 158-170.

[16] 张懿，刘旭，李海峰. 自适应图像直方图均衡算法[J]. 浙江大学学报（工学版）, 2007, 41(4): 630-633.ZHANG Y, LIU X, LI H F. Self-adaptive image histogram equalization algorithm[J]. Journal of Zhejiang University(Engineering Science), 2007, 41(4): 630-633.

[17] 朱立新，王平安，夏德深. 基于梯度场均衡化的图像对比度增强[J].计算机辅助设计与图形学学报, 2007, 19(12): 1546-1552.ZHU L X, WANG P A, XIA D S.Image contrast enhancement by gradient field equalization[J]. Journal of Computer-Aided Design &Computer Graphics, 2007, 19(12): 1546-1552.

[18] WANG C, YE Z. Brightness preserving histogram equalization with maximum entropy: a variational perspective[J]. Consumer Electronics,IEEE Transactions on, 2005, 51(4): 1326-1334.

[19] WONG H S, WANG J H. Contrast enhancement based on divided histogram manipulation[A]. 2000 IEEE International Conference on Systems, Man, and Cybernetics[C]. Nashville, TN, USA, 2002.

[20] ERAMIAN M, MOULD D. Histogram equalization using neighborhood metrics[A]. Proceedings of the 2nd Canadian Conference on Computer and Robot Vision[C]. Victoria, BS, Canada, 2005. 397-404.

[21] YOON B W, SONG W J. Image contrast enhancement based on the generalized histogram[J]. Journal of Electronic Imaging, 2007, 16(3): 1-8.

[22] 王炳健, 刘上乾, 周慧鑫等. 基于平台直方图的红外图像自适应增强算法[J]. 光子学报, 2005,(2): 299-301.WANG B J,LIU S Q,ZHOU H X,et al. Self-adaptive contrast enhancement algorithm for infrared images based on plateau histogram[J]. Acta Photonica Sinica, 2005,(2): 299-301.