以疑促思，构建高效数学课堂

尹江海

[摘  要] 学贵有疑. 贯穿数学教学始终的疑问具有激发学生思考的重要作用. 想要构建高效数学课堂、培养学生的学科素养、提升学生的思维品质，自然离不开“疑”的有效促进. 文章以“轴对称图形”的教学为例，从课堂氛围、情感体验与持续思考三方面谈以疑促思，构建高效数学课堂的具体方法.

[关键词] 轴对称图形;以疑促思;高效课堂

新课程标准明确提出：“新课改的关键性举措在于打破传统机械性或接受型学习模式，提倡在学生主动参与中积极动手、动口、动脑，在疑问中探究，在合作中学习[1]”由此可见，构建高效课堂的主要抓手在于以疑促思，最大限度地发挥学生大脑的功能，引领学生在疑问的不断产生、思考与解决中完成教学任务. 这是优化教学过程、整合三维目标、提高教学效率最好的方法，亦是促进学生全面发展的基本保障.

和谐的课堂氛围是以疑促思，

构建高效课堂的前提

俗话说：“学起源于思，思源于疑. ”思与疑是相辅相成的关系，思能促使疑产生，疑能促进思发展. 和谐舒适的课堂氛围是疑与思的温床，学生在良好的氛围中积极思考，并大胆想象、提出疑问. 课堂中，教师一个鼓励的眼神、一个善意的微笑、一句赞美的言语或一个不经意的动作都能激起学生内心疑的涟漪，从而积极思考. 一个充满欢笑、关爱、辩论与质疑的课堂，是学生不断产生疑问、积极思考并解决疑问的阵地.

教学片段1

为了让学生更直观地体会轴对称图形的性质与特点，笔者在课堂上开展了“设计白纸图案”的活动，以营造良好的课堂氛围，鼓励学生在动手操作中产生疑问并思考，以深化对知识的掌握.

师：请大家拿出事先准备好的纸张和剪刀. 现在我们进行今天的创意活动（学生都用期待的眼神看着老师）. 请大家将手中的纸张随便怎么折，然后进行剪或者撕，看看能得出什么样的图案.

生1：老师你看，王某的图案好丑.

师：哦？我来看看！还好啊，哪里丑了？

生2：他的图案是用手撕的，左、右不一样，不好看.

师：这个图案只是不那么完美而已，为什么你觉得难看呢？

生2：因为这个图的左、右两边不同.

生3：左、右两边不一样就不是对称图形了.

师（对王某说）：生1嫌弃你的图形不好看，是因为左、右不一样，对吗？（王某点头认同）但是老师觉得挺好看的，因为生活中除了有对称美，还有不对称美. （王某微笑）现在我们一起来看看其他同学的作品.

大家把自己的图案拿出来进行展示、对比.

生（齐）：好看的图形都是左、右能够重合的.

师：现在大家都认为对称的图形好看，那怎么描述对称图形呢？

生4：左、右两边一样的图形.

生5：对折后能完全重合的图形.

生6：以一条直线为分界，位于直线两侧的图形完全一样.

……

同学们对剪出来或撕出来的图形进行探讨与交流，然后逐渐获得轴对称图形的概念，思维在疑问的驱使下变得更为完整. 王某在教师善解人意的言语中也获得了学习的动力. 课堂活动的设置一定要低门槛，要给每个层次的学生提供参与的机会. 学生在平等、友好的氛围中，更容易促进元认知的发展■[2]. 在教师的鼓励与赏识中获得一种无形的精神力量，这比学到任何知识都重要.

真实可感的体验是以疑促思，

构建高效课堂的基础

对陌生事物产生好奇是人类的天性，也是疑问产生的主要来源之一. 教师根据学生的生活实际创设一些具有挑战性而又真实可感的教学情境，能有效地诱发学生新的认知冲突，从而促进学生思维的发展，提高课堂效率.

教学片段2

为了吸引学生的注意力，笔者先播放一段关于圆的动画，内容包括钟表内部的齿轮转动、骑行中自行车的车轮及转动中的轴承等，让学生感受圆的作用的同时，也让学生对圆产生更加直观、丰富的体验. 在此基础上展开相应的教学.

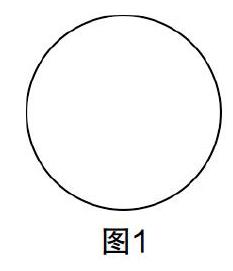
师：请大家开动脑筋想一想，如果我们想找到图1这个圆的对称轴，该怎么找.

生1：可以把这个圆的一半涂黑.

师：怎么知道多少是这个圆的一半？

生1：把这个圆折叠一下，就知道了.

生2：为什么要涂黑？直接折叠就行了.

生3：只要过图1的圆心画任意一条直线就行了.

师：很好！这个主意不错. 但是我们不知道这个圆的圆心在哪儿呀，你们有没有办法找到这个圆心？

生4：如图2，可以在这个圆上任取一条线段（弦）AB.

师：画完线段以后该怎么办呢？

生4：如图3，再作线段AB的垂直平分线CD.

师：到了这一步还是不能确定圆心，该怎么办呢？

生5：重复刚才的步骤，两条垂直平分线的交点就是这个圆的圆心.

师：太棒了！还有没有其他意见？

生6：我认为不需要重复刚才的步骤，只要作线段CD的垂直平分线，CD的垂直平分线和CD的交点就是圆心.

师：不错. 找到圆心后，过圆心的任意一条直线都是这个圆的对称轴.

此教学片段，教师巧妙地利用找圆心建立了圆的性质与轴对称概念之间的联系，学生亲身经历了寻找圆心的过程，这不但能让学生对知识的发生发展过程产生更加直观、深刻的印象，还对其思维的发展起到了良好的促进作用. 学生在积极的思考与亲身体验中获得了解决问题的不同方案，整个过程体现了学生的思维在问题中得以生长.

持续思考的习惯是以疑促思，

构建高效课堂的关键

发现疑问与提出疑问应贯穿教学的全过程. 学生每解决完一个疑问，新的疑问将会接踵而至，而新的疑问又成了学生思考的起点. 因此，教师应使用各种手段，不断地启发学生产生疑问并思考，以促使有深度的问题链的产生，让学生的思维在问题链中可持续发展. 所以，持续思考是实现以疑促思，构建高效课堂的关键.

教学片段3

在学生对轴对称的概念有了一定了解的基础上，教师可设计简单的数学实验，供学生产生有深度的问题链，从而让学生保持持续思考的状态，以促进思维的发展与课堂效率的提高.

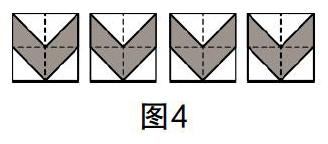
生活中的布匹、墙纸上的图案都是由小图案重复或拼接而来的，而小图案又是由更小的图案元素组合而成的. 现在我们将图4中的图案进行拼接，可得到各种图案.

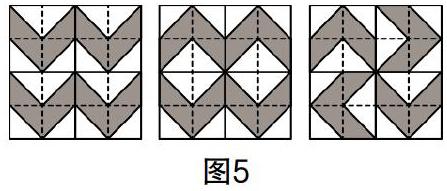
问题：（1）若拼接后的图案为图5所呈现的三种情况，请说一说其中具有旋转对称与轴对称特征的图案分别是哪个，并指出轴对称图案的对称轴.

（2）请尝试拼接出其他轴对称图案，并指出其对称轴.

学生经思考与拼接后获得了如图6的图案. 经讨论与分析后发现，一些成对出现的图案经旋转或翻转后还能出现重合的现象.

教师根据学生的最近发展区恰当地提出相应的问题，能在激发学生产生兴趣的同时促使学生产生新的求知欲. 正如苏霍姆林斯基所认为的那样，每个人的内心深处都希望自己是一个发现者、探索者与研究者[3]. 笔者紧抓学生的这种心理需求，引导学生主动参与轴对称知识的形成过程，将问題生活化的同时，由浅入深地引导学生逐渐形成问题链而持续地思考与分析，这样不仅拓展了学生的求知思路，还让学生的思维在释疑中得以有效发展.

总之，数学教学是学生获取知识、发现真理、答疑解惑的过程，作为教师，应尽可能地创造和谐的课堂氛围，让学生在真实可感的情感体验中形成持续思考的习惯. 学生在视、听、感、思等各个感觉器官的综合作用下经历设疑、质疑、释疑的思考过程，在以疑促思中构建高效的数学课堂，这能为其学习能力的可持续发展奠定坚实的基础.

参考文献：

[1]中华人民共和国教育部. 义务教育数学课程标准（2011年版）[S]. 北京：北京师范大学出版社，2012.

[2]张庆林，邱江. 思维和学习领域中的元认知研究[J]. 西南大学学报：社会科学版， 2005，31（1）.

[3]裴昌根，宋乃庆，刘乔卉，牟少星. 数学学习兴趣测评指标体系的构建与验证[J]. 数学教育学报，2018（02）.