基于深度学习的初中数学课堂教学探讨
谭晓玲
[摘 要] 深度学习能促进学生思维能力的发展,能提升学生的数学核心素养. 概述深度学习的背景、特点、基本策略及教学方法,同时,以“有理数的加法”教学进行积极实践后发现,运用深度学习这种教学方法,可以增强学生的思考力,丰富学生的数学思想方法,提升学生的核心素养.
[关键词] 深度学习;有理数;加法
何谓深度学习?具體到初中数学是指,重点掌握核心概念,把握数学知识的内在本质,深入研究知识背后的知识,使学生的思维能力与学习得到进一步发展. 其能够全面提升学生的数学核心素养,是学生终身学习之必需.
深度学习的由来及特点
深度学习开始于20世纪中期,正式提出这一概念是在1976年,经过几十年的实践与论证,现已进入成熟期. 学习的层次可分为知道、领会、应用、分析、综合、评价几个层次,其中浅层次学习是知道与领会,其是思维活动的基础,在这一层次上仅需传授知识即可. 与浅层次学习相对应的是深度学习,深度学习是指应用、分析、综合与评价,它是高阶思维活动[1]. 在初中阶段,深度学习具有以下明显特征:
(1)主动地理解和批判数学知识. 在理解所学数学知识的基础上,以质疑和批判的视角对待所学的新知识,将所学知识与原有的知识结构进行联结,通过不断地提问自己,加深对新知识的理解,以促进自身学习意识的提升.
(2)注重新知识的构建. 不同的学生有不同的知识背景,在深度学习形式下,通过调用已有的数学学习经验,将新旧知识连成一片,在深刻理解新知的同时,构建新知体系.
(3)注重知识与思想的整合. 深度学习是高阶思维活动,需要对知识进行整合. 数学知识本身不是零散存在的,它们之间的联系比较密切. 深度学习强调学生能够发现其中的内在本质,理清知识间的相互联系,通过技能的锤炼来深加工新知识,最终得到解决某一类数学问题的基本路径. 众所周知,容易忘记的是数学知识,但形成的技能会成为习惯,得到的数学思想会牢记终身,究其原因,是数学思想是事物本质的反映. 深度学习要求初中生掌握数学思想,以能终身受用.
(4)注重知识迁移的时效性. 行之有效的知识迁移是深度学习最重要的特征. 在初中生利用数学活动经验的时候,教师要为他们创设类似的情境,让他们由物及类,活学活用,用相同的策略解决更多的实际问题.
深度学习的基本策略及课堂教
学的基本方法
1. 深度学习的基本策略
(1)细化知识生成的过程
深度学习需要学生经历知识的生成过程. 简单表层的学习不是深度学习,教师应充分挖掘知识的生成过程,将学生置于具体情境中,留给学生充足的时间与空间,让他们去思考、去质疑、去揣摩.
(2)让学生的思维充分参与
所谓深度,主要是指探究思维有深度. 学生学习新知识时,只有充分调动大脑的神经元,让思维具有比较宽阔的广度及入木三分的深度,深度学习的真正意义才能实现. 学生思考量的大小决定了深度学习的程度.
(3)注重深度学习的反思
深度学习也注重学习方法,最重要的还是学生认知策略里的元认知策略. 在数学具体教学中,教师要关注元认知策略,学生要能够描述知识的产生过程,以及产生新知的过程中采用的是何种方式. 反思是深度学习的重要环节[2].
2. 深度学习课堂的教学方法
(1)提出的数学问题要具有开放性、探究性
与其他学科不同的是,数学知识是高度抽象的. 在“教师讲、学生听”的传统教学形式中,学生的思维是被动的,当学生被动接受知识时,将数学知识从具体的事物中抽象出来就显得比较困难. 因此,教师要体现学生的主体地位,与学生一起探究数学问题,在探究问题的过程中发现问题的答案,进而提高学生的学习兴趣,培养学生积极思维的意识[3].
如教学“平移”时,可以从学生熟悉的轴对称知识出发,它包括生活中的轴对称、轴对称的概念、轴对称的性质、运用轴对称作图. 可以将轴对称的学习知识网络迁移到平移的相关内容,引导学生比较轴对称与平移的异同,通过类比与迁移形成平移的知识网络,进而促进学生深度学习.
(2)设置体验式教学活动
体验式教学活动,指教师根据教学内容的特点,让学生在实践中体验学习,以出色地完成学习任务作为教学目标. 体验式教学活动的形式可以多样,以让学生更多地参与到学习中.
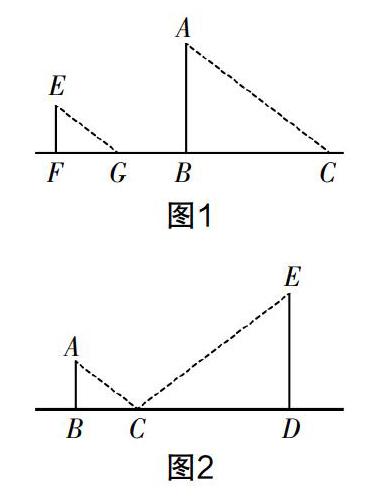
例如,学习“相似三角形的应用”时,可以组织学生从课堂走向实际生活,让学生分成两组,一组运用“同一时刻物高与影长成正比”测量校园内旗杆的高度,另一组则运用“镜面反射”测旗杆的高度. 如图1和图2.
基于深度学习的“有理数加法”
活动设计
1. 学习目标
(1)学生初步理解有理数加法在实际生活中的意义,掌握有理数加法法则,能够熟练运用有理数加法法则进行有理数的加法运算.
(2)学生经历有理数加法法则的探究过程,培养学生的观察比较能力、归纳概括能力,体会数形结合思想方法与分类思想方法.
(3)学生结合生活中的数学感受,进一步领略数学的价值,培养学生学习数学的兴趣.
2. 情境引入
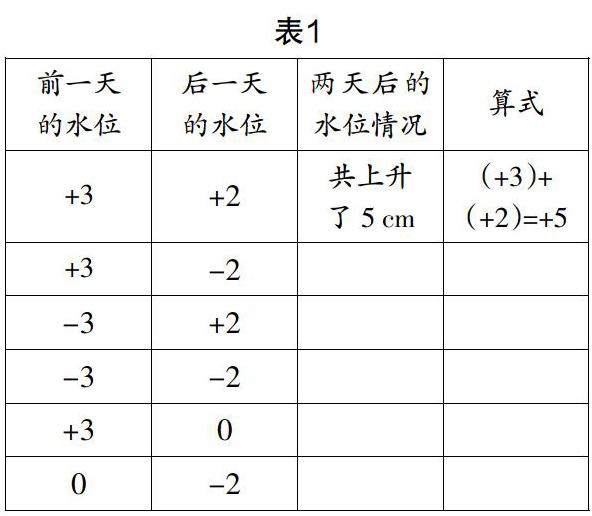
近期阴雨连绵,学校池塘里的水位在不时地变化. 有位善于观察生活的同学对近阶段池塘水位的变化做了详细的统计,统计表如表1.
设计意图?摇 使用贴近生活的实际问题来开始一节新课,能让学生体会到实际生活中存在数学问题,从而让数学为生活服务. 对此,学生可讲的话比较多.
3. 设计数学活动,引导学生发现和探索
数学活动:某台自动存取款机在某段时间处理了以下6项现款储蓄业务:存入2000元、支出1200元、存入1000元、存入2500元、支出500元、支出800元. 该台自动存取款机在这段时间现款的变化结果是怎样的?
设计意图 ?摇根据情境,学生从已有的活动经验出发,自主探究. 通过池塘里水位的变化,以及存取款机现款的变化情况,学生发现,这两道题的内容虽然不同,但本质是相同的. 这为有理数加法法则的形成做了伏笔.
4. 设计数学活动,解决问题
师:(1)某校足球队第一场比赛赢了3个球,第二场比赛赢了1个球. 这支足球队共赢了4个球,用数学式表达为(+3)+(+1)=+4.
(2)某校足球队第一场比赛输了3个球,第二场比赛输了1个球. 这支足球队共输了4个球,用数学式表达为(-3)+(-1)=-4.
请同学们说出其他可能的情况.
在此基础上,师生共同概括有理数加法法则:相同符号的两个数相加,符号不变,绝对值相加;异号两数相加,如果绝对值不相等,此时符号取绝对值较大的加数的符号,然后用较大的绝对值减去较小的绝对值;互为相反数的两个数相加,结果为0;一个数加上零,等于这个数.
5. 巩固提升
(1)计算:(+8)+(-17);(-17)+(-15);(-32.8)+(+51.76);(-3.07)+(+3.07).
(2)如果a=3,b=5,那么a+b=8吗?为什么?
(3)小明在一条东西走向的跑道上跑步. 他先向东跑了20 m,又向西跑了30 m,接着向东跑了10 m. 试根据题意列出算式,计算小明最后在什么位置,与原来的位置相距多少米.
设计意图?摇 第(1)题让学生直接根据有理数的加法法则进行运算,提高学生的运算能力;第(2)题将有理数加法与绝对值相结合,培养学生的说理能力与分类讨论思想;第(3)题让学生体會数学来源于生活,生活离不开数学.
数学核心素养的培养成为新时代的呼声,运用深度学习这种教学方法,可以强化学生的思考力,丰富学生的数学思想方法,提升学生的核心素养,能在内化学生数学知识体系的同时,不断提高学生的数学学习效率.
参考文献:
[1]王玲. 指向深度学习的初中数学教学设计研究[D]. 天津师范大学,2020.
[2]刘海英. 初中数学引导“深度学习”三策略[J]. 中学数学,2020(10).
[3]李光俊,张立珍. 深度学习理论下旋转变换的教学策略[J]. 中学数学教学参考,2020(11).

