双曲型脐点突变模型的向量场分析

荆小娜，赵立纯,*，刘敬娜

(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

R·Thom于1972年提出并系统地阐述了突变理论，给出了7类基本突变模型：折迭突变模型，尖角突变模型，燕尾突变模型，蝴蝶突变模型，椭圆型脐点突变模型，双曲型脐点突变模型，抛物型脐点突变模型.这些模型可以用来描述自然界中存在的大量突变现象，如地震[1]、火山爆发[2]、泥石流[3]、病虫害等的突然爆发.针对病虫害的突然爆发，赵慧燕等[4]建立麦蚜生态系统的折迭突变模型，利用势函数的极值解释了蚜虫种群数量在施药后骤变的现象.赵立纯等[5]基于尖角突变的性质将Logistic模型变换为尖角突变模型，并用微分方程定性理论对模型进行分析，得出突变发生的条件.李媛[6]利用微分方程定性理论分析了燕尾突变模型的突变特征.李桢[7]建立害虫种群动态的蝴蝶突变模型，通过势函数的极值来说明平衡点的稳定性，进而确定出控制点在分歧点集所处的区域.李建峰[8]通过建立害虫-天敌捕食系统椭圆突变模型，利用分歧点集的截线图和平衡点处的相轨线分析了模型的突变形式.

综上可知，上述涉及的折迭突变模型、尖角突变模型、燕尾突变模型、蝴蝶突变模型，其状态变量只有一个，且均用来刻画不同生态系统中害虫的突然爆发现象.对于椭圆型脐点突变模型、双曲型脐点突变模型和抛物型脐点突变模型，状态变量却有两个，而控制变量也均有三个，因此，对平衡点和分歧点集的分析有较大的难度.而这三类模型考虑的因素更多，如果能应用到病虫害的研究中，可能会为生态系统中的突变现象提供更好的解释，因此,本文选取双曲型脐点突变模型进行分析.

通过传统的方法分析模型会产生极大困难，本文利用Mathematica软件绘制的向量场图[9]分析模型的平衡点个数及稳定性变化情况，尝试揭示害虫种群的爆发现象.

1 模型的向量场分析

考虑双曲型脐点突变模型[10]

(1)

其中,x，y为状态变量，w，u，v为控制变量，相空间是五维空间(x，y，u，v，w).

由文献[10]知，分歧点集是关于w=0平面对称的，故应根据w=0，w>0，w<0三种情况绘制向量场图形.

情况1w=0

针对模型(1)，进一步取u>0，u=0，u<0三种情况来讨论：

情况1.1u>0

当w=0，u=1时，v分别取v=4，v=0，v=-2，得向量场图(见图1).

图1 w=0，u=1时平衡点附近的向量场

从图1可以看出，对w=0，u=1，当v由正连续变化到负时，模型的平衡点个数从4个变到0个，其中，A1为稳定结点，A2，A4为鞍点，A3为不稳定结点，B1，B2为鞍结点，说明w=0，u=1，v=0在模型的分歧点集上.

情况1.2u=0

当w=0，u=0时，v分别取v=4，v=0，v=-2，得向量场图(见图2).

图2 w=0，u=0时平衡点附近的向量场

从图2可以看出，对w=0，u=0，当v由正连续变化到负时，模型的平衡点从2个变到0个，其中，B3，B4为鞍结点，O为鞍点，说明w=0，u=0，v=0在模型的分歧点集上.

情况1.3u<0

当w=0，u=-1时，v分别取v=4，v=0，v=-2，得向量场图(见图3).

图3 w=0，u=-1时平衡点附近的向量场

从图3可以看出，对w=0，u=-1，当v由正连续变化到负时，模型的平衡点始终不存在，说明w=0，u=-1不在模型的分歧点集上.

情况2w>0

针对模型(1)，将参数u分为u>0，u=0，u<0三种情况来讨论：

情况2.1u>0

当w>0，u>0时，v在v>0，v=0，v<0三种不同情况下平衡点的变化情况不同，因此需根据这三种情况来分别分析.

情况2.1.1v>0

当w=1，u=1时，v分别取v=4，v=3.013 9，v=2，得向量场图(见图4).

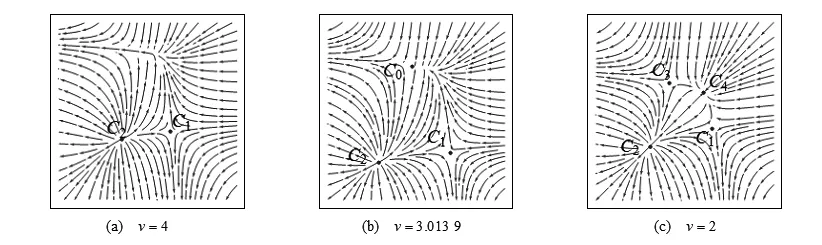
图4 w=1，u=1，v>0时平衡点附近的向量场

从图4可以看出，对w=1，u=1，当v逐渐减小时，模型的平衡点个数从2个变化到4个，其中，C0为鞍结点，C1，C3为鞍点，C2为不稳定结点，C4为稳定结点，说明w=1，u=1，v=3.013 9在模型的分歧点集上.

情况2.1.2v=0

当w=1，u=1，v=0时，得向量场图(见图5).

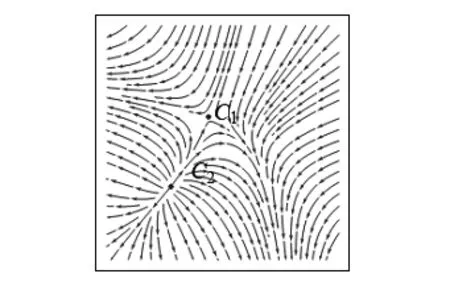
图5 w=1，u=1，v=0时平衡点附近的向量场

从图5可以看出，当w>0，u>0，v=0时，模型存在2个平衡点，其中C1为鞍点，C2为不稳定结点，而这与图4(a)平衡点的个数及稳定性一致.

情况2.1.3v<0

当w=1，u=1时，v分别取v=-0.1，v=-0.581 4，v=-2，得向量场图(见图6).

图6 w=1，u=1，v<0时平衡点附近的向量场

从图6可以看出，对w=1，u=1，当v逐渐减小时，模型的平衡点个数从2个变到0个，其中，C0为鞍结点，C1为鞍点，C2为不稳定结点，说明w=1，u=1，v=-0.581 4在模型的分歧点集上.

情况2.2u=0

当w=1，u=0时，v分别取v=4，v=-0.157 5，v=-2得向量场图(见图7).

图7 w=1，u=0时平衡点附近的向量场

从图7可以看出，对w=1，u=0，当v由正连续变化到负时，模型的平衡点个数从2个变到0个，其中，C0为鞍结点，C1为鞍点，C2为不稳定结点，说明w=1，u=0，v=-0.157 5在模型的分歧点集上.

情况2.3u<0

当w=1，u=-1时，v分别取v=4，v=2.986 1，v=-2,得向量场图(见图8).

图8 w=1，u=-1时平衡点附近的向量场

从图8可以看出，对w=1，u=-1，当v由正连续变化到负时，模型的平衡点个数从2个变到0个，其中，C0为鞍结点，C1为鞍点，C2为不稳定结点，说明w=1，u=-1，v=2.981 6在模型的分歧点集上.

情况3w<0

情况2分析了w>0时模型的平衡点个数及稳定性，那么对w<0时模型的分析将w取相反数.

情况3.1u>0

将v分为v>0，v=0，v<0三种情况来绘制向量场图.

情况3.1.1v>0

当w=-1，u=1时，v分别取v=4，v=3.013 9，v=2，得向量场图(见图9).

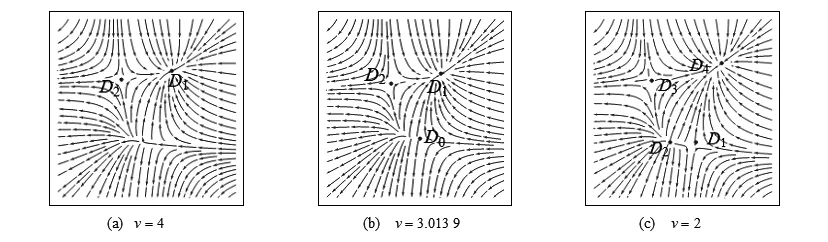
图9 w=-1，u=1,v>0时平衡点附近的向量场

注1 由于w>0与w<0时模型的分歧点集是对称的，因此不再重复叙述.

情况3.1.2v=0

当w=-1，u=1，v=0时，得向量场图(见图10).

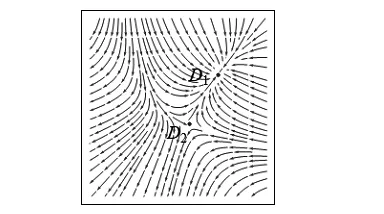
图10 w=-1，u=1，v=0时平衡点附近的向量场

情况3.1.3v<0

当w=-1，u=1时，v分别取v=-0.1，v=-0.581 4，v=-2，得向量场图(见图11).

图11 w=-1，u=1,v<0时平衡点附近的向量场

情况3.2u=0

当w=-1，u=0时，v分别取v=4，v=-0.157 5，v=-2,得向量场图(见图12).

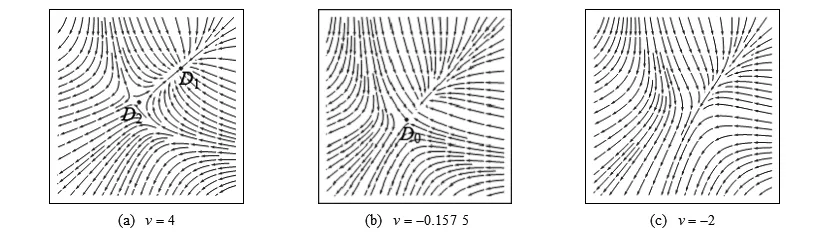
图12 w=-1，u=0时平衡点附近的向量场

情况3.3u<0

当w=-1，u=-1时，v分别取v=4，v=2.986 1，v=-2,得向量场图(见图13).

图13 w=-1，u=-1时平衡点附近的向量场

针对模型(1)，本节保持控制参数w，u取值不变，使参数v逐渐减少时，得到模型的平衡点变化情况，并根据平衡点个数的突然变化找到模型的分歧点集.

2 讨论与结论

由于双曲型脐点突变模型分歧点集的方程太过复杂，不能直接从方程得到模型的突变形式，因而本文利用向量场图刻画模型平衡点的变化状况，且能观察到模型的分歧点集，进而揭示出模型在整个控制空间中的突变行为.

针对双曲脐点突变模型，在第一部分中已经讨论了当控制参数w，u不变，而v逐渐减少时，模型平衡点的变化状况.根据情况2.1.1，情况2.2，情况2.3，从向量场图可以看出保持控制参数w，v不变，当u变化时，模型平衡点的个数及稳定性的变化，如图4(a)→图7(a)→图8(a).