多维探究典型问题 培养学生发散思维
上海市行知中学(201999)范广哲
不等式作为高中数学重要内容之一, 有着广泛的应用.不等式的综合应用对培养学生的数学抽象、数学运算、逻辑推理等数学核心素养有着重要作用.
多角度探究问题可以培养学生细致的观察力、丰富的联想力和创造性的思维能力.在平时的教学过程中,教师应积极引导学生对数学问题进行多角度、多层次、多维度地进行分析,提高学生对知识的迁移和运用能力,有效地培养和发展学生的发散思维和创新思维.
教师在平时教学过程中,应积极引导学生注重解决数学问题的通性通法,培养学生联系数学基础知识、洞察数学问题本质的能力,才能更有效地落实数学课程的育人目标与育人价值.笔者在平时教学过程中,发现有一类三元最值问题在大学自招及高中数学竞赛中时常出现,本文给出这类典型问题的一般形式及多种解法,希望能给读者带来一些思考和启发.
题目已知x1,x2,x3∈R+, 常数k1,k2,k3,m2,m3∈R+,求S=的最大值.
解以下证明:Smax=当且仅当x1:x2:x3=时等号成立.
解法一(先柯西不等式后基本不等式)由于表达式具有齐次性,设其中k >0.

因而S≤当且仅当x1=x2=时等号成立.
解法二(先柯西不等式后三角换元)不妨设k1x21+k2x22+k3x23=k2,其中k >0.

令x1=其中θ ∈则

解法三(三角换元法)设其中k >0,则设


解法四(球坐标法)设=k2,其中k >0,设

当且仅当x1=x3=时等号成立.
解法五(拉格朗日函数法)设k1x21+k2x22+k3x23=k2, 其中k >0, 构造拉格朗日函数L(x1,x2,x3,λ)=m2x1x2+m3x1x3+λ(k1x21+k2x22+k3x23-k), 下面对L(x1,x2,x3,λ)分别求关于x1,x2,x3,λ的一阶偏导并分别令其等于零,可得

解得
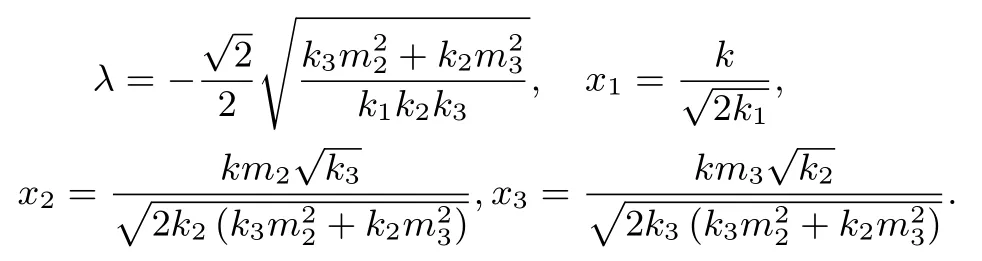
这就是拉格朗日函数的稳定点, 可得此值为函数的最大值,代入可得Smax=
解法六(配方法)由题设:k1x21+k2x22+k3x23=从而
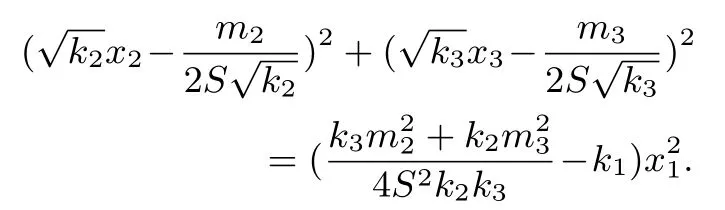
解法七(待定系数法)引入参数λ, 满足λ ∈(0,k1).设相加得,设

即S≤当且仅当x1:x2:x3=:k1k3m2:k1k2m3时等号成立.
解法八(先基本不等式后柯西不等式)

解法九(判别式法)由题设得到将其视作x1的一元二次方程,方程有实根.因而,Δ = (m2x2+m3x3)2-由柯西不等式可得
一是配套政策和法律制度不健全,当前针对绿色债券的相关法律制度尚未完全形成,缺少财税优惠政策以及政府为主导的担保机制和风险补偿机制。二是绿色债券产品较为单一,当前我国绿色债券主要以绿色金融债为主,绿色资产证券化、绿色债券指数产品发展较为滞后。三是融资成本偏高,受2017年初债券市场利率走高的影响,市场流动性趋弱,绿色债券融资成本增加。占比最多的AAA级和AA+主体发行利差与同级别普通债券相比多为负,融资成本偏高。

即S≤当且仅当x1:x2:x3=k1k3m2:k1k2m3时等号成立.
推论已知x1,x2,x3∈R+, 常数k1,k2,k3,m2,m3∈R+, 且满足= 1, 则S=m2x1x2+m3x1x3的最大值为Smax=
以下给出如上结论的应用..
例1(2020年《数学通讯》问题征解第2 期437 问题)已知x,y,z为正数,若不等式4x2+y2+3z2≥λ(2xy+3yz)恒成立,求λ的最大值.
分析由于求最大值,因而考虑正数情况.在结论中令k1=1,k2=4,k3=3,m2=2,m3=3,则即λ的最大值为1.
例2(2019年上海交大自主招生)已知x,y,z不全为0,求的最大值.
分析由于求最大值,因而考虑正数情况.在结论中令k1=k2=k3=1,m2=1,m3=2,则
例3(2016年高联福建预赛)已知x,y,z >0, 求的最大值.
分析在结论中令k1=k2=k3= 1,m2= 4,m3= 1,则
例4(2015年《数学教学》947 问题)已知x2+y2+z2=1,求xy+2xz的最大值.
分析由于求最大值,因而考虑正数情况.在推论中令k1=k2=k3=1,m2=1,m3=2,则Smax=
例5(2012年高联甘肃预赛)已知x2+y2+z2=1,求xy+yz的最大值.
分析由于求最大值,因而只考虑正数情况.在推论中令k1=k2=k3=m2=m3=1,则Smax=
例6(2009年高联浙江预赛)已知x2+y2+z2=1,求的最大值.
分析由于求最大值,因而只考虑正数情况.在推论中令
最后,给出其n元推广形式,有兴趣的读者可自行证明.
变式(n元形式)已知x1,x2,··· ,xn ∈R+, 常数k1,k2,··· ,kn,m2,m3,··· ,mn ∈R+, 其中n≥3,n ∈N,求的最大值.
结论(Sn)max=
注若n= 2 时,(S2)max=其结果与上式亦吻合.

