双绝对值一次函数的作图及应用

甘肃省白银市平川中学(730700)李映林

“不等式选讲”是部分省份高考数学选考的内容之一,近几年考查的重点是绝对值不等式的解法与最值,以及不等式的证明.

而在绝对值不等式的解法及最值中,双绝对值一次函数f(x)=k1|x-x1|+k2|x-x2|频频“登场”,是当之无愧的不等式选考命题的“网红”.

一般地,关于解f(x)=k1|x-x1|+k2|x-x2|≥(≤)C(其中C为常数)型不等式的通法是零点分段法; 求函数f(x)=k1|x-x1|+k2|x-x2|最值的方法主要由两种,其一仍然是零点分段法;其二是绝对值(三角)不等式法.

我们若能从整体上掌控函数f(x)=k1|x-x1|+k2|x-x2|的图象, 然后再灵活地综合上述方法, 数形结合,就可以达到事半功倍的效果.

一、函数f(x)=k1|x-x1|+k2|x-x2|图象总述

为了行文方便,在函数f(x)=k1|x-x1|+k2|x-x2|中,我们不妨设k1/=k2,x1＜x2.

口诀粗分三类详为八,系和为零台阶型,系和为正是V型,系和为负是Λ 型.

说明1口诀中的“系和”是指k1+k2.

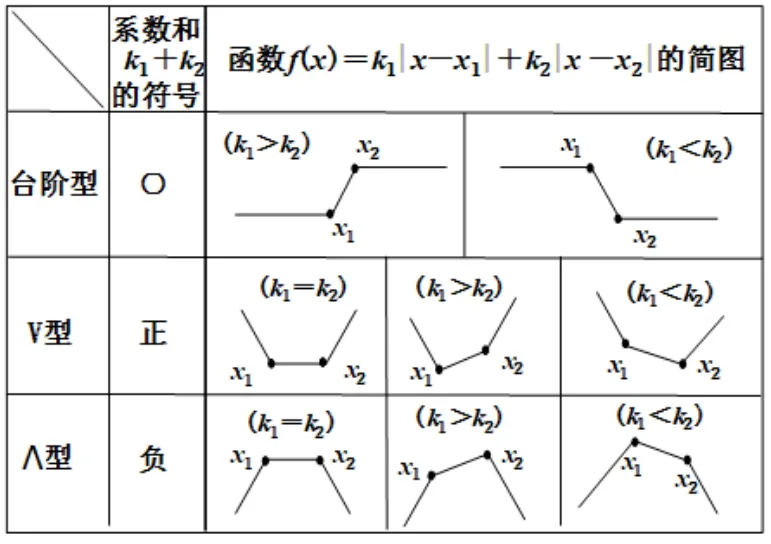
图1

说明2这里V 型和Λ 型是对函数单调性的形象表述.

说明38 个图像中左折点(x1,f(x1))与右折点(x2,f(x2))的高低问题.规律是: 系数大的折点, 位置低;系数相等,折点高度相同.可总结为: 系大点低等同高.

笔者认为: 实际操作时, 通过比较f(x1)与f(x2)的大小,来判定两个折点位置的高低,比采用上述规律的方法更加方便简捷.

二、函数f(x)= k1|x-x1|+k2|x-x2|图象的画法——四点三线法

由零点分段法可得

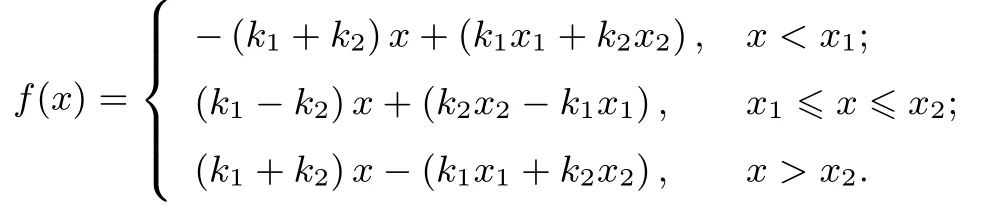
从而函数f(x)的图象是由三段直线型的折线构成的.所以有如下画法——四点三线法

第一步: 描出四个关键点.

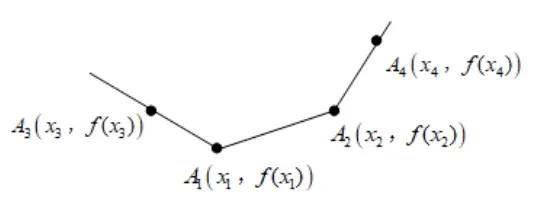
图2

第一个点是左折 点A1(x1,f(x1));第二个点是右折点A2(x2,f(x2)); 第三个点是左辅助点A3(x3,f(x3)),该点必须在左折点A1的左侧,只需x3＜x1即可.第四个点是右辅助点A4(x4,f(x4)),该点必须在右折点A2的右侧,只需x2＜x4即可.

第二步: 连成三段线.

从左到右,依次连接射线A1A3,线段A1A2,射线A2A4,即可成图.

例1(2020年高考全国Ⅰ卷理科第23 题第一问)已知函数f(x)=|3x+1|-2|x-1|.

(1)画出y=f(x)的图像

分析(1)因系数和k1+k2= 3-2＞0, 故图像是V型;(2)易得左折点右折点A2(1,4); 左辅助点不妨取A3(-1,-2), 右辅助点不妨取A4(2,5);依次连接射线A1A3,线段A1A2,射线A2A4成图.

解因f(x)=作出图象,如图3 所示.

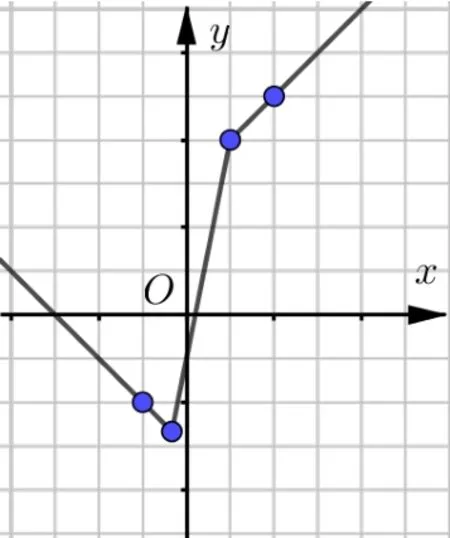
图3

例2(2016年高考全国Ⅰ卷理科第24 题第一问)已知函数f(x)=|x+1|-|2x-3|.

(1)画出y=f(x)的图像.

分析(1)因系数和k1+k2= 1-2＜0,故图像是Λ型.(2)易得左折点A1(-1,-5);右折点左辅助点不妨取A3(-2,-6),右辅助点不妨取A4(2,2).依次连接射线A1A3,线段A1A2,射线A2A4成图.

解因f(x)=作出图象,如图4 所示.

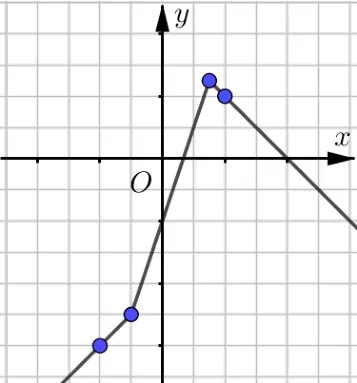
图4

三、图象的应用

在处理与双绝对值一次函数函数f(x)相关的不等式、最值等问题时,借助其的图像,使代数问题几何化,即直观简洁,又通俗易懂,具有“一目了然”的优势,不失为是一种较好的方法.

例3(2017年高考全国Ⅲ卷理科第23 题第一问)已知函数f(x)=|x+1|-|x-2|.

(1)求不等式f(x)≥1 的解集;

分析(1)因系数和k1+k2= 0,故图像是台阶型.(2)易得左折点A1(-1,-3); 右折点A2(2,3),左辅助点不妨取A3(-2,-3),右辅助点不妨取A4(3,3),然后依次连线成图.

解因f(x)=故函数f(x)的图像如图5 所示.故所求解集为[1,+∞).

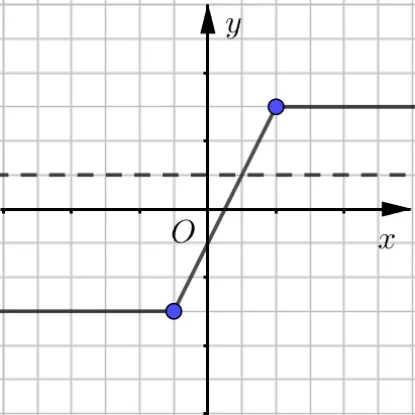
图5

例4(2014年高考安徽卷理科第9 题)若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为

A.5 或8 B.-1 或5 C.-1 或-4 D.-4 或8

解法1该题解法甚多,被大多数考生采用解法是零点分段法,但操作量较大.现抄录如下:

(ⅰ)当a ＜2 时,f(x)=易得f(x)在(-∞,-上单调递减, 在,+∞)上单调递增, 故f(x)mⅰn=f(-1|= 3,a=-4 或a=8(舍)

(ⅱ)当a=2 时,f(x)=3|x+1|≥0,与题意不符,舍去.

(ⅲ)当a ＞2 时,f(x)=易得f(x)在上单调递减, 在上单调递增, 故f(x)mⅰn=f= 3,a= 8 或a=-4(舍).

综上,a=-4 或a=8.所以选D.

解法2由上述给出的上绝对值一次函数图像作法——四点三线法, 可知函数f(x)的最值, 来自于左右两个折点.所以f(x)mⅰn== 3, 从而或解得a ∈∅或a=-4 或a= 8.所以选D.

例5(2020年高考全国Ⅰ卷理科第23 题第二问)已知函数f(x)=|3x+1|-2|x-1|.

(2)求不等式f(x)＞f(x+1)的解集.

分析(1)将函数f(x)的图象(见例1 图3)向左平移1个单位,可得函数f(x+1)的图象,如图5 所示.(2)求出交点由图6 可得所求解集为

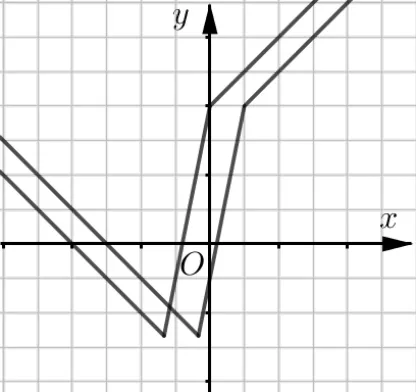
图6

例6(2018年高考全国Ⅲ卷理科第23 题)设函数f(x)=|2x+1|+|x-1|.

(1)画出y=f(x)的图像.

(2)当x ∈[0,+∞)时,f(x)≤ax+b,求a+b的最小值.

分析(1.1)因系数和k1+k2=2+1＞0,故图像是V型.(1.2)易得左折点右折点A2(1,3),左辅助点不妨取A3(-1,3),右辅助点不妨取A4(2,6),然后依次连线成图.

解因f(x)=故函数f(x)的图像如图7 所示.

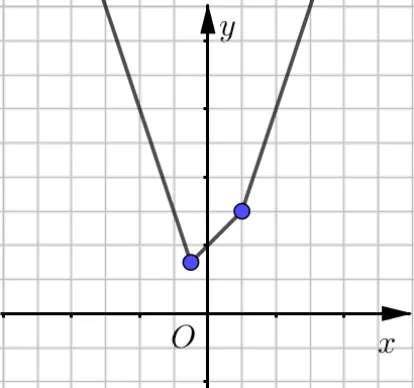
图7

分析(2.1)在图7 中的右半面,动直线y=ax+b,只需不低于函数f(x)的图像即可.即动直线y=ax+b的斜率a不小于直线y=3x的斜率3,且其y轴上的截距b不小于2 即可.

解由图7 可得:a≥3,b≥2,当a= 3,b= 2 时,a+b取最小值为5.

双绝对值一次函数f(x)=k1|x-x1|+k2|x-x2|,在高考中,命题形式单一、稳定,解题的思路比较固定,对选考不等式选讲的同学们而言,是个重要的得分点,所以要加深理解,重点突破.而掌握函数f(x)图像的总规律,及用四点三线法快速准确地画出其简图,是顺利解决问题的关键所在.