同构变换在高考中的应用

广东省湛江一中培才学校(524037) 魏 欣

同构变换的思想,是高中数学中的重要的思想方法之一,是我们解决数学问题的利器,在数列、解析几何、不等式、函数与导数的应用中无处不在,方法更是多种多样,灵活巧妙,要求解题者具备较深的数学功底和数学智慧.本文探究了同构变换的思想的一些独特而巧妙的应用,以求给大家一些新的启发,拓展思维视野,感悟数学方法之美妙.

一、在数列中的应用

求递推数列的通项公式的关键就是将递推公式变形为“依序同构”的特征,即关于(an,n)与(an-1,n-1)的同构式,从而将同构式设为辅助数列便于求解.

例1(2020年高考全国Ⅲ卷理科第17 题第(1)问)设数列{an}满足a1=3,an+1=3an-4n.求数列{an}的通项公式.

解析由an+1= 3an -4n, 可得an+1-(2n+ 3)=3[an-(2n+1)],即

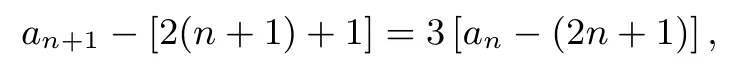
令bn=an -(2n+1),则bn+1= 3bn, 则数列{bn}的首项b1=a1--3 = 0.于是,数列{bn}所有各项都为0,所以bn=an -(2n+ 1)= 0.所以数列{an-(2n+1)}是各项为0 的常数列.所以数列{an}的通项公式an=2n+1(n ∈N*).

点评解决本题的关键在于构造同构式

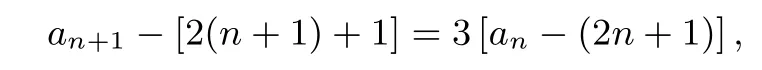
得到数列{an-(2n+1)}是各项为0 的常数列.从而巧妙求出数列{an}的通项公式.

例2(2014年高考广东卷理科第21 题第(2)小问)设数列{an}的前n项的和为Sn,满足:Sn= 2nan+1-3n2-4n(n ∈N*),S3=15.求数列{an}的通项公式.

解析因为Sn=2nan+1-3n2-4n,所以

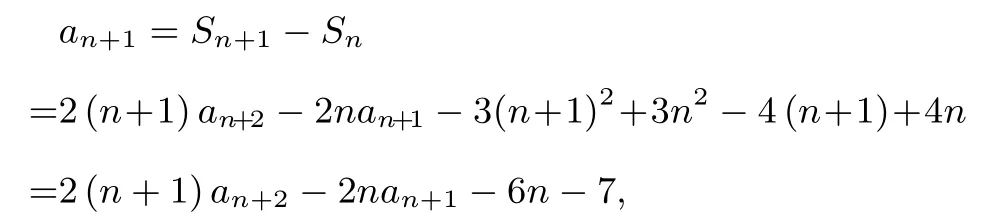
从而得到: (2n+2)an+2=(2n+1)an+1+6n+7,即

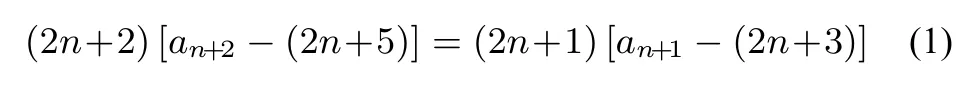
因为a1= 3, 所以a1-5 = 3-(2×1+1)= 0,所以数列{an-(2n+1)}是各项都为零的常数列, 所以an= (2n+1).所以数列{an}的通项公式为an=(2n+1)(n ∈N*).

点评以上解法中,通过构造同构式(1),巧妙地得到数列{an-(2n+1)}是各项为0 的常数列.从而很快求出数列{an}的通项公式.

二、在解析几何中的应用

如果A(x1,y1),B(x2,y2)满足直线或曲线的方程为同构式,则A、B为方程所表示直线或曲线上的两点.特别地,若A(x1,y1)、B(x2,y2)满足ax1+by1+c=0,ax2+by2+c=0,则直线AB的方程为ax+by+c=0,这种设而不求的思想也是同构式的体现.

例3(2020年高考全国Ⅰ卷解析几何题)已知A,B分别为椭圆E:+y2= 1(a ＞1)的左、右顶点,G为E的上顶点,= 8,P为直线x= 6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(1)求椭圆E的方程;(2)证明: 直线CD过定点.

解析(1)椭圆E的方程为+y2=1(过程略).

(2)设直线CD的方程为x=ty+n,-3＜n ＜3,设C(x1,y1),D(x2,y2),点P(6,m).联立得(9 +t2)y2+ 2tny+n2-9 = 0.由韦达定理有y1+y2=由A,C,P三点共线,可得

由D,B,P三点共线,可得

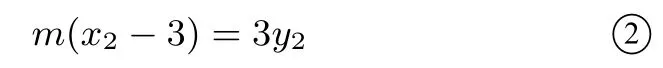
由①式和②式, 可得3y1(x2-3)=y2(x1+ 3), 所以3y1y2(x2-3)=(x1+ 3).又=所以(x1+3)(x2+3)+27y1y2=0,即

(t2+27)y1y2+t(3+n)(y1+y2)+(3+n)2=0.y1+y2=所以(t2+27)(n2-9)-2t2(n2+3n2)+(n+3)2(t2+9)=0,解得n=或n=3(舍).综上,直线CD过定点

点评此法的关键在于方程3y1(x2-3)=y2(x1+3)的两边乘以y2,构造多个同构式,然后再将得到的方程右边的整体代换掉,得到了关于y1+y2,y1y2,n的方程,再通过少量的运算便得到了定点.设而不求,构造同构式,自然流畅.

例4(2019 全国Ⅲ卷文科第21 题第(1)问)已知曲线C:y=,D为直线y=上的动点,过D作曲线C的两条切线,切点分别为A,B.证明: 直线AB过定点.

解 析(Ⅰ)设D(x0,-),A(x1,y1), 则y1=又因为y=所以y′=x.则切线DA的斜率为x1,故y1+=x1(x1- x0), 整理得2x0x1-2y1+ 1 = 0.设B(x2,y2), 同理得2x0x2-2y2+ 1 = 0.A(x1,y1),B(x2,y2)都满足直线方程2x0x -2y+ 1 = 0.于是直线2x0x -2y+ 1 = 0 过点A,B, 而两个不同的点确定一条直线, 所以直线AB方程为2x0x -2y+ 1 = 0.即2x0x+ (-2y+ 1)= 0, 当2x= 0,-2y+ 1 = 0 时, 即x=0,y=等式恒成立.所以直线AB恒过定点

点评以上解法中,A(x1,y1)、B(x2,y2)两点同时满足构造的同构式直线方程2x0x-2y+1=0,使得问题轻松解决!

三、在函数和不等式中的应用

将题目中的等式或不等式经过适当的整理变形,表示成两侧结构相同的形式,则可由相同的结构构造函数,进而与函数的单调性找到联系,据此可用来比较变量大小或解函数不等式和证明函数不等式.可归纳如下的常见三种类型.

类型一: 地位同等要同构,主要针对双变量

含有地位同等的两个变量x1,x2,或x,y的等式或不等式,如果进行整理(即同构)后,等式或不等式两边具有结构的一致性,往往暗示构造函数应用单调性解决.

1.对于含有二元变量x1,x2的函数,可以使变量x1,x2分别位于不等式两边, 呈现出不等式左右两边结构一样的对称关系式, 则可将相同的结构构造为一个新函数, 进而结合该函数的单调性等性质,可比较大小或解不等式.如由f(x)±g(y)＞f(y)±g(x),变形为f(x)±g(x)＞f(y)±g(y),于是构造函数F(x)=f(x)±g(x),所以F(y)=f(y)±g(y),所以利用函数F(x)的单调性解题.

例5(2020年高考全国Ⅰ卷理科第12 题)若2a+log2a=4b+2log4b,则( )

A.a ＞2bB.a ＜2bC.a ＞b2D.a ＜b2

解析因为2a+ log2a= 4b+ 2log4b= 22b+ log2b,而22b+ log2b ＜22b+ log2b+ 1 = 22b+ log22b, 所以2a+log2a ＜22b+log22b.构造函数f(x)= 2x+log2x,由指数、对数函数的单调性,可得f(x)在(0,+∞)内单调递增,且f(a)＜f(2b),所以a ＜2b.故选B.

点评在上题中, 通过添加常数1, 经过放缩变形,使等式变为不等式, 且不等式两边具有相同的结构f(x)= 2x+ log2x的形式, 然后利用函数的单调性就可以顺利解决问题.

例6(2020年高考全国Ⅱ卷理科第11 题文科第12 题)若2x-2y ＜3-x-3-y,则( ).

A.ln(y-x+1)＞0 B.ln(y-x+1)＜0

C.ln|x-y|＞0 D.ln|x-y|＜0

解析由2x-2y ＜3-x-3-y,可得,2x-3-x ＜2y-3-y.构造函数f(x)=2x-3-x,由指数函数的单调性,可得f(x)在R 内单调递增,且f(x)＜f(y),所以x ＜y,即y-x ＞0.因为y-x+1＞1,所以ln(y-x+1)＞ln 1=0.故选A.

点评在上题中,经过移项变形,使不等式两边具有相同的结构f(x)= 2x -3-x的形式,然后利用函数的单调性就可以顺利解决问题.

2.在含有多个变量的问题中,往往根据问题的需要,选定其中的一个变量为“主元”,其他变量暂时视为常数,这种方法就是“主元”角色的转化,是解决多变量问题的一个重要方法.

含有二元变量x1,x2的函数,常见同构类型有以下三种:

(1)g(x1)- g(x2)＞ λ[f(x2)- f(x1)]⇔ g(x1)+λf(x1)＞g(x2)+λf(x2),构造函数φ(x)=g(x)+λf(x);

(2)＞k(x1＜x2)⇔f(x1)-f(x2)＜kx1- kx2⇔ f(x1)- kx1＜ f(x2)- kx2, 构造函数φ(x)=f(x)-kx;

(3)(x1＜ x2)⇔ f(x1)-f(x2)＞构造函数φ(x)=f(x)+

例7(2018年高考全国Ⅰ卷理科第21 题)设函数

(Ⅰ)讨论f(x)的单调性;

(Ⅱ)若f(x)存在两个极值点x1和x2, 证明:

解析(Ⅰ)当a ＞2 时,f(x)在(0,x1),(x2,+∞)上单调递减,f(x)在(x1,x2)上单调递增(x1,x2为f′(x)= 0 的两根);当a≤2 时,f(x)在(0,+∞)上单调递减.(过程略)

(Ⅱ)由(Ⅰ)可知a ＞2,x1=0＜x1＜1＜x2,x1+x2=a ＞0,x1·x2=1.

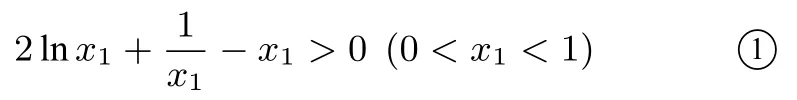
构造函数g(x)= 2 lnx+- x(0＜x ＜1), 则g′(x)=＜0.所以g(x)在(0,1)上单调递减,g(x)＞g(1)=2 ln 1+-1=0,即g(x)＞0,所以①式成立.所以＜a-2.

点评构造函数运用导数判断函数单调性时, 关键是根据解题需要和已知信息构造出适合的函数.在上述解法中, 同构式2 lnx1+- x1＞0(0＜x1＜1), 构造函数g(x)=2 lnx+-x(0＜x ＜1),再由单调性和最值易证.

类型二: 指对跨阶想同构,同左同右取对数

对于一个指数、一次函数、对数三阶的问题可以通过跨阶函数的同构,转化为两阶问题解决.通常在一些求参数的取值范围、零点个数、证明不等式中应用跨阶同构来快速解题.跨阶同构需要构造一个母函数,即外层函数,这个母函数需要满足: 1.指对跨阶;2.单调性和最值易求.

指对跨阶同构的基本模式有:

1.积型:aea≤blnb,一般有三种同构方式:

(1)同左:aea≤blnb ⇔aea≤(lnb)elnb, 构造函数f(x)=xex;

(2)同右:aea≤blnb ⇔ealn ea≤blnb, 构造函数f(x)=xlnx;

(3)取对数:a+lna≤lnb+ln(lnb),构造函数f(x)=x+lnx.

说明在对“积型”进行同构转化时,取对数是最快捷的,而且构造出的函数,其单调性一看便知.

例8(2018年高考全国Ⅰ卷文科第21 题第(2)问)已知函数f(x)=aex-lnx-1.证明: 当a≥时,f(x)≥0.

解析证明: 当a≥时,f(x)≥ex -lnx-1,要证f(x)≥0,只要证明-lnx-1 ≥0,即证ex≥e ln(ex),即证xex≥exln(ex), 即证exln ex≥exln(ex).构造函数g(x)=xlnx,只要证明x ＞0 时,g(ex)≥g(ex).由g′(x)=lnx+1,易见g(x)在单调递减,在,+∞)单调递增.当时,g(ex)=xex ＞0,g(ex)=exln(ex)＜0,恒有g(ex)≥g(ex)成立;当结合g(x)在,+∞)单调增,得g(ex)≥g(ex)成立.

综上,当a≥时,f(x)≥0.

点评有些不等式可通过条件结论分析入手,细致观察,抓住不等式的结构特征,变为左右两边结构相同的不等式类型,便可构造出特征函数,这样就有利于找到解题的突破口,然后利用函数的单调性解决.

(3)取对数:a-lna ＜lnb-ln(lnb),构造函数f(x)=x-lnx.

例9(2017年高考全国Ⅰ卷理科第11 题)设x,y,z为正数,2x=3y=5z,则( )

A.2x ＜3y ＜5zB.5z ＜2x ＜3y

C.3y ＜5z ＜2xD.3y ＜2x ＜5z

解析设2x= 3y= 5z=k(k ＞1), 则2x=因为lnk ＞0,只需比较的大小.注意到所以只需比较的大小.构造函数f(x)=则f′(x)=可见f(x)在(0,e)递减,在(e,+∞)递增,3,4,5∈(e,+∞)且3＜4＜5,所以即5z ＞2x ＞3y.

点评把需要比较的量转化为结构相同的形式, 即2x=发现只需比较函数思想下自然会想到f(x)=结合导数判断其单调性,用其单调性比较出的大小.构造函数的思路来自于抽象出所要比较量的共同结构,只有抽象出共同结构才能发现所需构造的函数.

3.和差型: ea±a ＞b±lnb,一般有两种同构方式:

(1)同左: ea±a ＞b±lnb ⇔ea±a ＞elnb±lnb,构造函数f(x)=ex±x;

(2)同右: ea±a ＞b±lnb ⇔ea±ln ea ＞b±lnb,构造函数f(x)=x±lnx.

例10(2020年山东卷第21 题第(2)问)已知函数f(x)=aex-1-lnx+ lna.若f(x)≥1, 求a的取值范围.

解析由f(x)≥1, 可得aex-1-lnx+ lna≥1, 即ex-1+lna-lnx+lna≥1,亦即ex-1+lna+x-1+lna≥lnx+x=elnx+lnx.构造函数g(t)=et+t,则g′(t)=et+1＞0,所以g(t)在R 上单调递增,且g(x-1+lna)≥g(lnx),所以x -1 + lna≥lnx, 即lna≥lnx - x+ 1.构造函数h(x)=lnx-x+1,则h′(x)=当0＜x ＜1时,h′(x)＞0,所以h(x)单调递增;当x ＞1 时,h′(x)＜0,所以h(x)单调递减.所以h(x)≤h(1)= 0,所以lna≥0,所以a≥1.故a的取值范围为[1,+∞).

点评在上题中,经过指对转换、移项变形,使不等式两边具有相同的结构g(t)= et+t的形式,然后利用函数的单调性就可以顺利解决问题.

类型三: 无中生有去同构,凑好形式是关键

对于有些式子无法直接进行变形同构, 往往需要凑常数、凑参数或凑变量(如: 同乘x或同加x)等方式转化为类型二解决.

此种类型常见模式有:

1.式子两边同乘x.如aeax ＞lnx,一般在式子两边同乘x(无中生有),变形为axeax ＞xlnx,后面的转化同类型二的情形1.

2.式子两边同加x.如ex ＞aln(ax-a)-a ⇔lna(x-1)-1⇔ex-lna-lna ＞ln(x-1)-1,同时加x(无中生有), 变形为ex-lna+x-lna ＞ln(x-1)+x-1 =eln(x-1)+ln(x-1),等价于x-lna ＞ln(x-1).

3.式子两边互为反函数.如ax ＞logax ⇔exlna ＞⇔(xlna)exlna ＞xlnx,后面的转化同类型二的情形1.

说明因为ax ＞logax两边互为反函数, 而互为反函数的两个函数图像关于y=x对称, 所以还可以这样转化ax ＞logax ⇒ax ＞x ⇒lna ＞

例11(2018年全国高中数学联赛天津赛区预赛)已知a ＜0,不等式xa+1·ex+alnx≥0 对任意的实数x ＞1 恒成立,则实数a的最小值是( ).

解法1由题意得xa+1·ex+alnx≥0⇒xex≥构造同构函数g(x)=xex, 易知g(x)单调递增对x ＞1 恒成立, 等价于g(x)≥=-e,即a≥-e.故选D.

解法2由题意得xa+1·ex+alnx≥0⇒xex≥⇒exln ex≥x-alnx-a, 构造同构函数g(x)=xlnx, 易知g(x)单调递增对x ＞1 恒成立, 等价于g(ex)≥g(x-a), 即ex≥x-a, 即a≥=-e,即a≥-e.故选D.

解法3由题意得xa+1·ex+alnx≥0⇒xex≥⇒x+lnx≥-alnx+ln(-alnx),构造同构函数g(x)=x+lnx,易知g(x)单调递增对x ＞1 恒成立,等价于g(x)≥g(-alnx),即x≥-alnx,即a≥=-e,即a≥-e.故选D.

点评在上题中,经过移项变形,使不等式两边具有相同的结构的形式,三种方法构造三个同构函数,然后利用函数的单调性就可以顺利解决问题.

类型四: 同构放缩需有方,切放同构一起上

对解决有些指对混合不等式问题,往往要结合切线放缩,或换元法,进行局部同构,这样可以大大降低这类问题的难度,但要注意取等号的条件以及常见变形等.

同构基础上的切线放缩模型常见的有:

1.ex≥x+1,ex≥ex型:xex= ex+lnx≥x+lnx+1,xex= ex+lnx≥e(x+lnx);= ex-lnx≥x-lnx+1,=elnx-x≥lnx-x+1;xnex=ex+nlnx≥x+nlnx+1,xnex=ex+nlnx≥e(x+nlnx).

2.lnx≤x-1,lnx≤型:x+lnx=ln(xex)≤xex-1,x+lnx=ln(xex)≤xex-1;x+nlnx=ln(xnex)≤xnex-1,x+nlnx=ln(xnex)≤xnex-1.

例12(2018年高考全国Ⅰ卷文科第21 题第(2)问)已知函数f(x)=aex-lnx-1.证明: 当a≥时,f(x)≥0.

解析先证明: ex-1≥x,lnx≤x-1.

令g(x)=ex-1-x,h(x)=lnx-(x-1)(x ＞0),g′(x)= ex-1-1,h′(x)=所以g(x)在(-∞,1)递减, 在(1,+∞)递增,h(x)在(0,1)递增, 在(1,+∞)递减, 所以g(x)≥g(1)= 0,h(x)≤h(1)= 0, 所以ex-1≥x,lnx≤x -1.要证f(x)≥ 0 成立, 只需证-lnx-1 ≥0,只需证:

而ex-1≥x,lnx≤x-1,所以ex-1-lnx-1 ≥x-(x-1)-1=0,所以(*)成立,所以当a≥时,f(x)≥0.

点评以上解法利用了高考中常考的两个经典函数不等式ex-1≥x,lnx≤x-1,能避免讨论参数的范围的复杂的运算.两个经典不等式函数ex-1≥x,lnx≤x-1.

同构变换为我们解题带来了新思路、新视野,其解法灵活、巧妙、简捷、新颖,给人带来美的享受和震撼,也使人们的思维在更广阔的空间得到发展,对培养人们积极思考、善于观察、勇于创新、追求简单的探究精神大有裨益.其实数学中有很多知识之间有某种规律和内在联系,可能由于我们认知水平的有限, 这种内在联系还处在未知状态还没有被发觉.因此,在学习过程中,要始终保持积极的探究状态,努力探索知识的内在联系,在深度和广度上多下功夫,这是学习应该具备的优秀品质,正如布鲁纳所说: 学习知识就是学习事物是怎样相互关联的.