理清概念关键点 让错误不再重演——辨析二项分布与超几何分布

甘肃省天水市清水县第六中学(741400) 何少杰

在人教A 版数学选修2-3 中学生分别学习了超几何分布和二项分布两节内容,由于近年笔者在所在学校连续担任高三复读班数学教学工作,在接连几年的模考阅卷过程中发现,对超几何分布和二项分布发生混用的现象普遍存在.尽管是不同届的学生,却在同一类问题中栽了跟头,这不由得引发了我的反思: 如何消除学生心中的疑惑,避免在这一类问题上重蹈覆辙,让错误不再重演! 为此我翻阅了不同教材中对两种分布的定义,查阅了相关资料,对两种分布的区别与联系进行了整理,并对为何错解中的结果正确进行了说明.

一、题目、错解与问题

题目1某精准扶贫帮扶单位, 为帮助定点扶贫村真正脱贫, 坚持扶贫与扶智相结合, 帮助精准扶贫户利用互联网电商渠道销售当地特产苹果.苹果单果直径不同单价不同,为了更好的销售, 现从该精准扶贫户种植的苹果树上随机摘下50个苹果测量其直径,经统计,其单果直径分布在区间内(单位mm),统计的茎叶图如图所示:

(Ⅰ)从单果直径落在[72,80)的苹果中随机抽取3 个,求这3 个苹果单果直径均小于76mm 的概率;

(Ⅱ)以此茎叶图中单果直径出现的频率代表概率.直径位于[65,90)内的苹果称为优质苹果,对于该精准扶贫户的这批苹果,某电商提出两种收购方案:

方案A:所有苹果均以5 元/千克收购;

方案B:从这批苹果中随机抽取3 个苹果,若都是优质苹果,则按6 元/千克收购; 若有1 个非优质苹果,则按5 元/千克收购;若有2 个非优质苹果,则按4.5 元/千克收购;若有3个非优质苹果,则按4 元/千克收购.

请你通过计算为该精准扶贫户推荐收益最好的方案.

题目2新冠疫情期间,停课不停学,各学校组织上网课的同时为了解学生的课外学习时间,教育局从某所学校高二年级1000 名学生中随机抽取了100 名学生,调查了一周的课外学习时间X.其中X ～N(9,1.32).

(Ⅰ)估计本周该高二年级学生课外学习时间在10.3 小时以上的人数(保留整数);

(Ⅱ)从本校高二年级学生中随机抽取5 人,求恰有3 人的课外学习时间超过10.3 小时的概率(结果保留两位小数).

模考阅卷中发现不少学生在两道题的第(Ⅱ)问出现了下面的错解:

题目1(Ⅱ)的错解方案B 中,50 个苹果中有40 个优质苹果,记Y为随机抽取的3 个苹果中优质苹果的个数,随机变量Y的取值为0,1,2,3.则

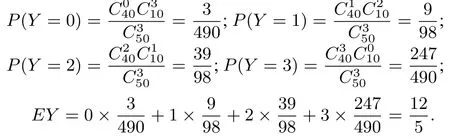
方案A 中5 元/千克收购价相当于B 方案中随机抽取3个苹果有2 个优质苹果.因为EY=所以通过比较可知方案B 收益更好.

题目2 (Ⅱ)的错解由(Ⅰ)知在高二年级1000 名学生中, 课外学习时间在10.3 小时以上159 人, 不超过10.3小时共841 人, 记Y为随机抽取的5 人中课外学习时间在10.3 小时以上的人数, 则Y服从超几何分布, 所以P(Y=3)=

为了分析错解,我们再给出两问的正解.

题目1(Ⅱ)的正确解法方案B 中,由题意以此茎叶图中单果直径出现的频率代表概率,从这批苹果中随机抽取1 个苹果,取出优质苹果的概率为记Y为随机抽取3 个苹果中优质苹果的个数,则Y ～B(3,因此,得到

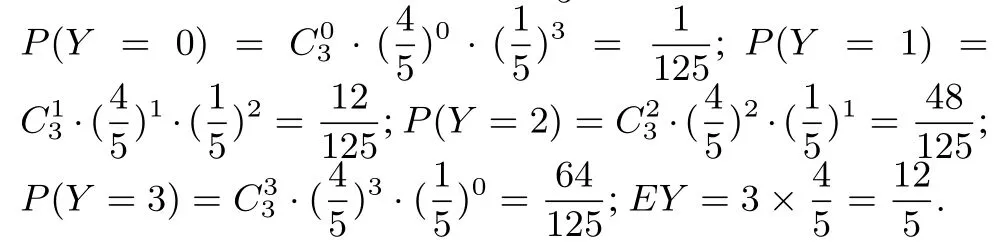
方案A 中5 元/千克收购价相当于B 方案中随机抽取3个苹果有2 个优质苹果.因为EY=所以通过比较可知方案B 收益会更好.

题目2(Ⅱ)的正确解法由(Ⅰ)知在高二年级1000 名学生中,任取1 人,学习时间超过10.3 小时的概率为0.1587,记Y为随机抽取的5 人中课外学习时间在10.3 小时以上的人数,则Y ～B(5,0.1587),所以P(Y=3)=C35·(0.1587)3·(1-0.1587)2≈0.03.

模考以后我对这两道题为何学生会出现误判两种分布的情况进行了考查, 发现他们主要出现了下面的几个问题:(1)第1 题中对“从这批苹果中随机抽取3 个苹果”理解出现偏差,错解中一部分学生把“这批苹果”错误的理解为随机摘下的50 个苹果,属于审题不严造成的错解.(2)两道题中一部分学生看到“抽取”二字,不分青红皂白马上肯定地认为考查的是超几何分布,造成错解.(3)有一部分学生考虑到了抽取的方式是无放回抽取,符合超几何分布的抽样模型,所以他认为一定是超几何分布,而没有考虑到尽管都是无放回抽样,但总体数目都很大,抽取少量样本时可以认为每一次抽样中条件都未发生改变,是典型的二项分布,属于对两种分布的概念不清造成的错解.那么这两种分布的本质区别是什么? 为何它们的数学期望一致呢? 如何在解题时避免误判呢?

二、剖析两种分布的不同点与相同点,关注概念本质区别与联系

1.概念不同

超几何分布 一般地, 在含有M(M≤N)件次品的N件产品中, 任取n(n≤N)件产品, 离散型随机变量X表示这n件产品中的次品数, 则事件{X=k}发生的概率P(X=k)=, (k= 0,1,2,··· ,m), 其中m= mⅰn{M,n}且n≤N,M≤N,n,M,N ∈N*,于是随机变量X的分布列具有表1 的形式,则称随机变量X服从参数为n,M,N的超几何分布,记作X ～H(n,M,N).

表1

二项分布 一般地, 若一次试验只有两个可能的结果A或, 事件A发生的概率为p, 事件发生的概率为q=1-p,在n次独立重复试验中,离散型随机变量X表示这n次独立重复试验中事件A出现的次数,则事件{X=k}发生的概率P(X=k)=,其中k=0,1,2,··· ,n,0＜p ＜1,于是随机变量X的分布列具有表2 的形式,则称随机变量X服从参数为n,p的二项分布,记作X ～B(n,p)

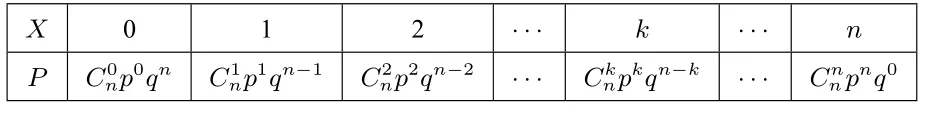
表2

2.随机试验的条件不同

超几何分布在试验过程中必须给定总体数,而且总体必须由数目明确的“正品”与“次品”两类构成.

二项分布进行的试验无需知道总体数.

3.随机试验类型与特点不同

超几何分布进行的随机试验是在含有M(M≤N)件次品的N件产品中,任取n(n≤N)件产品,它包含了n次试验,是满足古典概型的随机试验,即每个基本事件发生的可能性都相等,基本事件的总数是有限的.这n次试验中第一次是从N件产品中任取1 件,第二次从N -1 件产品中任取1 件,……,因此每一次试验都会相互影响,不是独立重复试验.

二项分布进行的随机试验是在同一条件下进行的n次独立重复试验.

4.随机试验的模型与结果不同

超几何分布进行的随机试验是无放回抽样模型,每一次试验的结果数较多,比如在有3 件次品的10 件产品中任取1件产品,不同的结果有种.

二项分布进行的随机试验是重复试验,所以每次抽取条件不变,可以理解为有放回抽样模型.而且每一次试验只有两个对立的结果A或,称为伯努利试验.

5.随机变量X表示的事件不同

超几何分布中离散型随机变量X表示抽取出的这n件产品中的次品数.所以事件{X=k}表示抽取的n件产品中有k件次品,n-k件正品.

二项分布中离散型随机变量X表示这n次独立重复试验中事件A出现的次数,即成功次数.所以事件{X=k}表示n次独立重复试验中事件A出现了k次,事件出现了n-k次.

6.随机变量X表示的事件概率计算公式不同

超几何分布进行的随机试验是满足古典概型的随机试验,所以事件{X=k}发生的概率P(X=k)=其中k=0,1,2,··· ,m,m=mⅰn{M,n}.

二项分布中进行的是独立重复试验, 满足独立事件的概率乘法公式, 所以事件{X=k}发生的概率P(X=k)=(1-p)n-k,其中k=0,1,2,··· ,n.

7.随机变量X的概率计算条件不同

超几何分布概率计算会在题设中给出抽样个数n、总体数N,会给出或可求出总体中两类产品中的“次品”数M.

二项分布概率计算会在题设中暗示给出或者可求出成功概率p.

8.随机变量X的数学期望公式不同

(1)若X ～H(n,M,N),则EX=

证明由

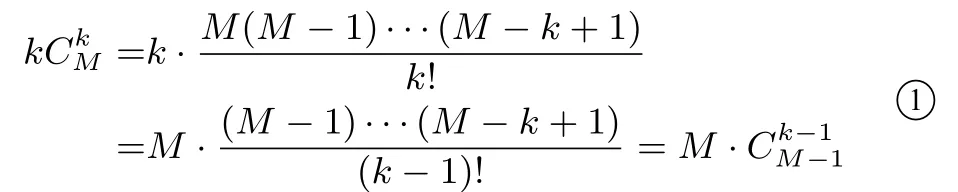
则EX=为从含有M件次品的N件产品中取出一件次品以后, 抽取n -1 件产品的不同取法种数, 故所以,证毕.

(2)若X ～B(n,p),则EX=np.

证明同①有则

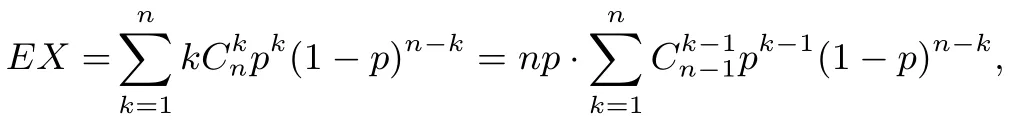
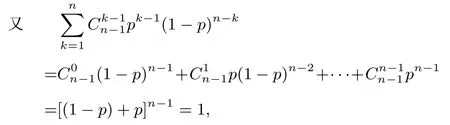
所以EX=np,证毕.

因为在n次独立重复试验中A事件发生的概率为p,所以可以理解为一次随机试验中A事件平均发生p次,则在n次独立重复试验中A事件平均发生np次.

9.两种分布的相同点

(1)两者都是离散型随机变量分布,且随机变量都只能取非负整数值.

(2)错解与正解中两者的数学期望会相等.正因为如此,在抽样问题中出现答案貌似“正确”, 但却是错解的现象以后,有些同学甚至很坚定地认为自己的错解是正确的.究其原因是在题目中取到“次品”概率p=所以错误的解法也会得到正确的期望值.

10.两种分布之间的联系

当总体数N较小时,无放回抽样中按照超几何分布计算的概率与有放回抽样中按照二项分布计算的概率差异比较明显,当总体数N不断变大时两种分布计算的概率逐渐接近,当总体数N无限或很大时,此时无放回抽取少量样品对次品率的影响很微小,次品率p此时是一个稳定值,两种分布计算的概率相等,即

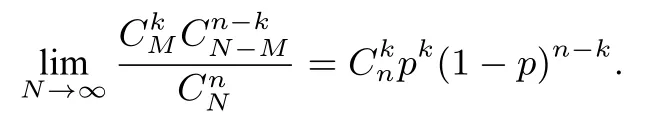
证明因为

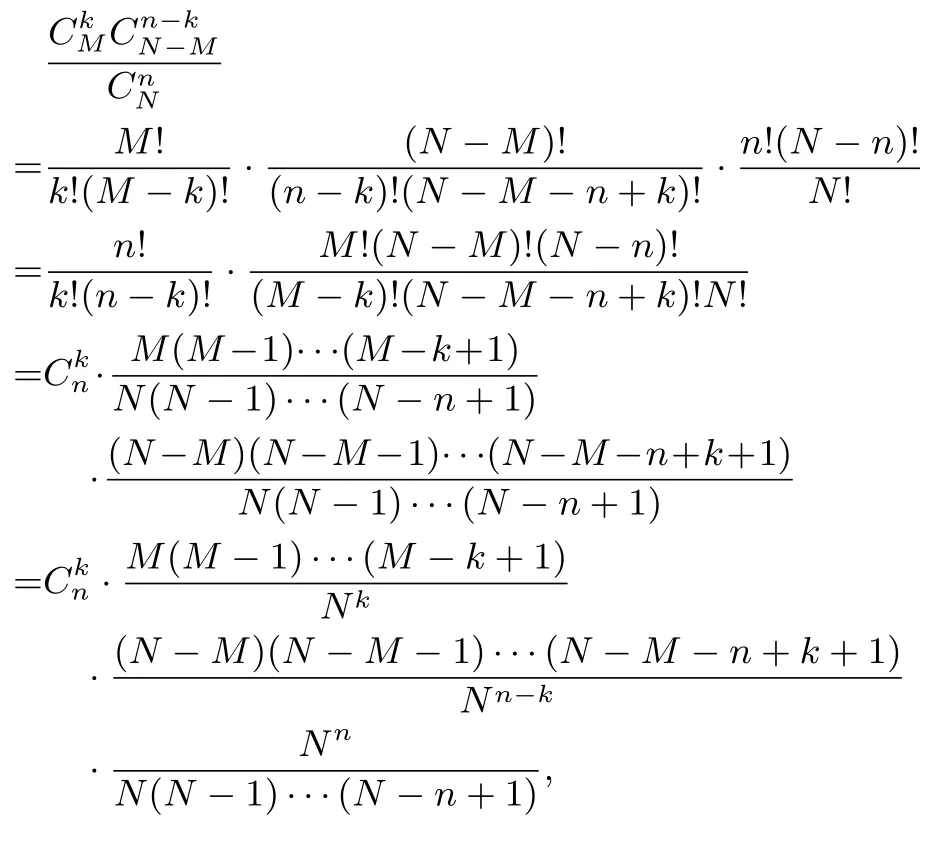
又n,k是常数,则

因此判断两种分布时, 不能机械地以抽样方法来判定,对于总体数N很大的这种抽取,尽管是无放回抽样,但超几何分布已经近似为二项分布了,我们都把它看成是n次独立重复试验,按照二项分布来解题.

三、如何避免发生两种分布的误判

要避免发生两种分布的误判,除了需要在知识方面强化对两种分布概念的理解与辨析,理清概念的本质区别,提高对两种分布的辨识力之外,笔者发现学生还普遍存在审题不严的问题,由于概率统计题目包含文字较多,加之部分题目中条件可能会以图表的形式给出,在紧张的考试过程中,他们就更加难以从繁冗的已知条件中找准关键字句提取重要信息,往往凭借并不完善的经验选取概率模型解题,但基于两种分布在一定的条件下可以相互转化的特点,学生在解题时极易发生两种分布的误判,所以为了避免发生误判还需培养良好的审题习惯,找准题目中的关键字句进行分析,跳出题目设置的“陷阱”,走出认识误区.那么为了让错误不再重演,如何审题才能避免发生两种分布的误判? 通过以上对两种分布的概念解读,不难发现在判断两种分布时需要做到以下五“看”:

(1)看总体数是否给出,未给出或若给出总体数较大一般考查二项分布.

(2)看一次抽取抽中“次品”概率是否给出,若给出或可求出一般考查二项分布.

(3)看一次抽取的结果是否只有两个结果,若只有两个对立的结果A或,一般考查二项分布.

(4)看抽样方法,如果是有放回抽样,一定是二项分布;若是无放回抽样,需要考虑总体数再确定.

(5)看每一次抽样试验中,事件是否独立,事件发生概率是否不变,若事件独立且概率不变,一定考查二项分布,这也是判断二项分布的最根本依据.

四、总结与建议

概率统计本身是一部分既难教又难学的知识,其中不乏一些似是而非又违背直观感觉的易混内容,就高中阶段学生的认知水平而言更加难以驾驭.而教材作为众多专家智慧的结晶,是广大教师与学生的第一手资料,其中的案例都是经过仔细挑选,反复锤炼过的经典案例,这些案例都承载着很强的教育功能,很多高考题目源于教材中的经典案例,这就要求教师在教学中从教材出发,紧扣概念,深入钻研教材中的经典案例,把握好不同知识之间的内在联系与本质区别.

对于高中教材中出现的容易混淆的基本概念: 随机性、确定性;频率、概率;稳定于、趋近于;古典概型、几何概型;互斥事件、独立事件等,作为新增教学内容,初学概率统计时非常容易将新概念联系到自己的生活经验中,往往这些概念在生活中的定义与数学定义不完全一致,会有一定的偏差,从而产生认识误区,所以教学时应该结合具体实例对学生的认知加以引导,对错误的认知加以矫正,通过具体实例加深对概念的理解,最终走出误区,彻底吃透概念.事实上,概念教学应该是数学教学的重中之重, 概率统计的教学也不例外,因为数学概念是数学思维形成的起点,对数学概念的理解与运用是数学思维能力得以发展的核心.

对于高中教材中出现的三种离散型随机变量服从的分布: 两点分布、二项分布、超几何分布,最关键的是要让学生正确区分其对应的随机试验模型,理清概念的关键点,让他们意识到这三种分布的联系.当独立重复试验中的试验次数n=1 时,二项分布就会化为两点分布,超几何分布的极限分布是二项分布;对于概率模型的正确选择,可以尝试分类集中训练,让学生通过具体的问题情境感知到它们之间的区别与联系,在教师的指导下逐渐有所感悟.

对于高中教材中出现的连续型随机变量分布——正态分布,可以在教学时指出当二项分布中成功概率p= 0.5 时,二项分布的分布图是对称的,这种情况下当n逐渐增大时,二项分布从分布图可以看到会越来越接近于正态分布,也就是说二项分布的极限分布是正态分布,了解这些知识不仅可以让他们更清楚地认识概念的源与流,从而提高对几种分布的辨识能力,避免发生模型混用的错误,而且还能为以后学生的进一步学习奠定良好的基础.