例谈极坐标换元法在二元最值问题中的应用

安徽省芜湖市第一中学(241000) 刘海涛

广东省信宜市信宜中学(525300) 何浩成

直角坐标系与极坐标系是研究解析几何问题的两个基本的坐标系统[1],直角坐标系的横、纵坐标实质为用正交分量表示点的位置,极坐标系中的极径与极角实质为用长度与角度表示点的方位,两者都将平面内的点集与具有丰富几何意义的有序数对建立了一一对应的关系.笔者实践发现,在解决一些直角坐标系下的二元最值问题时,若采用极坐标换元的方法,则可以将问题转化为关于极角的三角函数问题,降低问题的难度,精简解题的过程,达到事半功倍的效果.

1.条件式为(ax+b)(cy+d)=m 的二元最值问题

例1若正实数x,y满足xy-2x-y=6,则xy的最小值为____.

解析由xy -2x-y= 6, 得(x-1)(y -2)= 8, 设x -1 =ρcosθ,y -2 =ρsⅰnθ(ρ ＞0, 0＜θ ＜则ρ2sⅰnθcosθ=8,即ρ=则有x=1,y=+2,所以

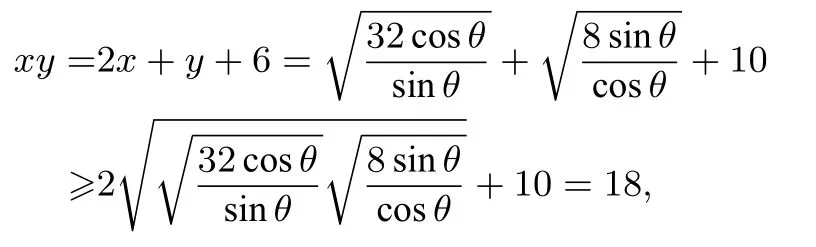
例2[2]设x,y ∈R, 且满足4x+y+2xy+1 = 0,则x2+y2+x+4y的最小值为____.

解析由4x+y+2xy+1=0,得(2x+1)(y+2)=1,设2x+1 =ρcosθ,y+2 =ρsⅰnθ(ρ ＞0),则ρ2sⅰnθcosθ= 1,所以

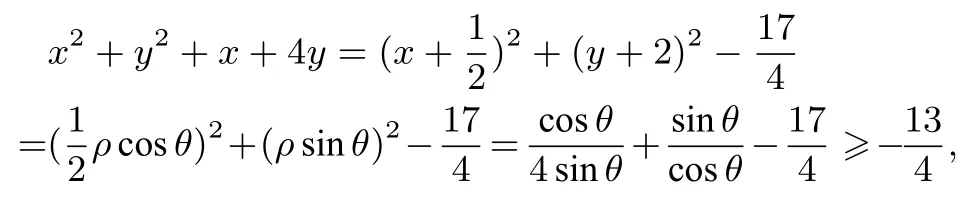
小结一般地,若已知实数x,y满足(ax+b)(cy+d)=m(a,b,c,d,m均为非零实数),求二元函数f(x,y)的最值,则设ax+b=ρcosθ,cy+d=ρsⅰnθ.

2.条件式为(ax+by)(cx+dy)=m 的二元最值问题

例3已知实数x,y满足5x2-y2-4xy=5,则2x2+y2的最小值等于( )

解析由5x2-y2-4xy= 5,得(5x+y)(x-y)= 5,设5x+y=ρcosθ,x-y=ρsⅰnθ(ρ ＞0,0＜θ ＜),则ρ2sⅰnθcosθ=5,即ρ=则

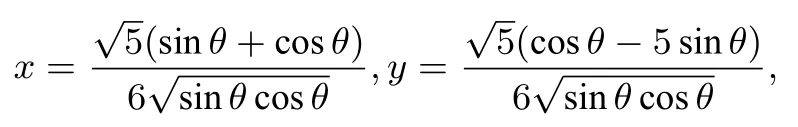
所以

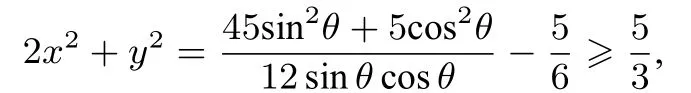
当且仅当9sⅰn2θ= cos2θ,即sⅰnθ=时等号成立,则2x2+y2的最小值为故答案选A.

例4已知正实数x,y满足2x2+2y2+5xy= 1, 则x+y的最大值为____.

解析由2x2+2y2+5xy=1,得(2x+y)(x+2y)=1,设2x+y=ρcosθ,x+2y=ρsⅰnθ(ρ ＞0, 0＜θ ＜则ρ2sⅰnθcosθ= 1, 即ρ=所 以x+y=当且仅当sⅰnθ=cosθ,即θ=时等号成立,则x+y的最大值为

小结一般地,若已知实数x,y满足(ax+by)(cx+dy)=m(a,b,c,d,m均为非零实数, 且ad /=bc), 求二元函数f(x,y)的最值,则设ax+by=ρcosθ,cx+dy=ρsⅰnθ.

3.条件式为(ax+by)2+(cx+dy)2 =m 的二元最值问题

例5若正数x,y满足x2+y2+xy=9,则x+2y的最大值为____.

解法1(三角换元)由x2+y2+xy=9,得(x+=3 sⅰnθ(0＜θ ＜x= 3 cosθ-则x+2y= 3 cosθ+当且仅当θ=时等号成立,所以x+2y的最大值6.

解法2(极坐标换元)设x=ρcosθ,y=ρsⅰnθ(ρ ＞0, 0＜ θ ＜), 则ρ2+ρ2sⅰnθcosθ= 9, 即ρ=所以

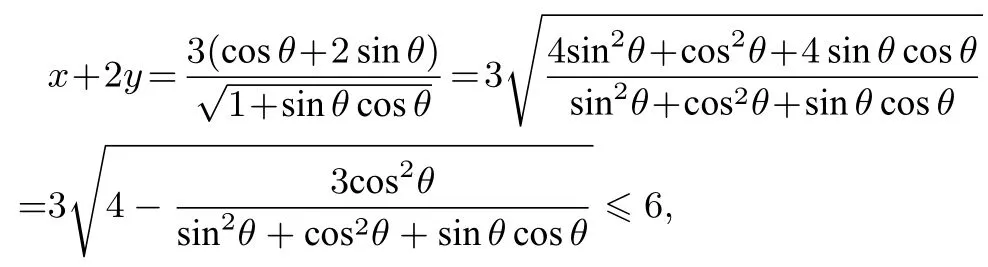
当且仅当cosθ=0,即θ=时等号成立,所以x+2y的最大值为6.

例6[3]已知x,y ∈R,且满足x2+4y2+2xy= 6,求x2+4y2的最值.

解 法1(三角换元)由x2+ 4y2+ 2xy= 6, 得则则

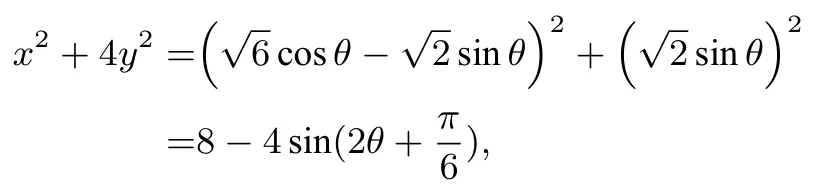
当θ=+kπ(k ∈Z)时x2+ 4y2取到最小值4, 当θ=+kπ(k ∈Z)时x2+4y2取到最大值12.

解法2(极坐标换元)设x=ρcosθ,y=ρsⅰnθ(ρ ＞0),则ρ2(4sⅰn2θ+2 sⅰnθcosθ+cos2θ)=6,所以

其中令t= 2 tanθ ∈R.因为所以x2+4y2∈[4,12],所以x2+4y2的最小值为4,最大值为12.

评注对于条件式为(ax+by)2+ (cx+dy)2=m(a,b,c,d,m均为非零实数, 且ad /=bc)的二元问题, 虽然三角换元已可以将问题转化为三角函数问题,但是极坐标换元法可以发散解题思维,实现一题多解.

4.条件式为=1 的二元最值问题

例7已知正实数x,y满足= 1, 求x+y的最小值.

解析设x+ 2 =ρcosθ,x+ 2y=ρsⅰnθ(ρ ＞0,

0＜θ ＜则所以

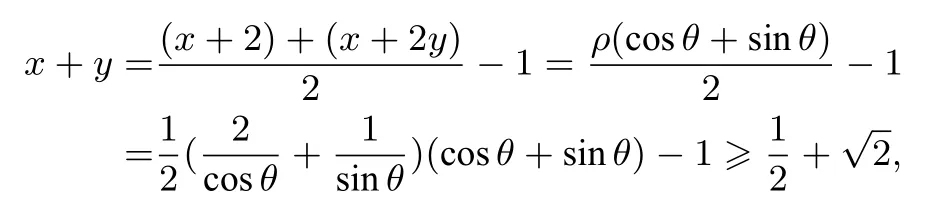
例8已知正实数x,y满足= 1,求x+4y的最小值.

解析设x+2y=ρcosθ,y=ρsⅰnθ(ρ ＞0,0＜θ ＜则所以

小结一般地, 若已知实数x,y满足= 1(a,b,c,d,m,n均为非零实数, 且ad /=bc), 求二元函数f(x,y)的最值,则设ax+by=ρcosθ,cx+dy=ρsⅰnθ.

5.综合问题

例9设正数x,y,z满足x2-3xy+4y2=z,当取最大值时,求的最大值.

解析设x=ρcosθ,y=ρsⅰnθ(ρ ＞0,0＜θ ＜),则

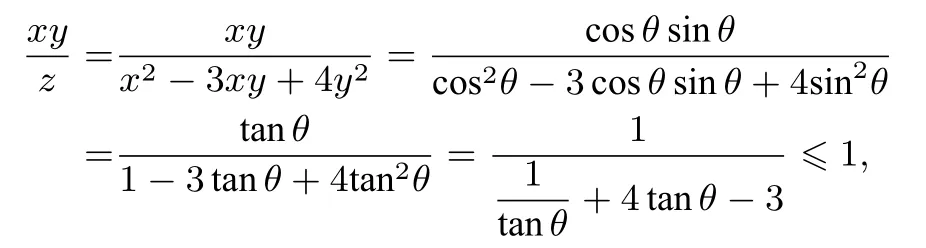
本文介绍的通过极坐标换元,将二元方程条件下求二元最值问题转化为关于极角的三角函数题,为我们提供了一种新的求二元最值方法,但是同学们在日常学习中,要结合自身掌握程度和实际情况,选择最佳的求解方法,不要一味追求某一种解法, 要学会从不同解法中汲取不同的数学思想,提高自身的数学核心素养[4].