高考数列综合题的三种新题型归类分析

福建省宁德市民族中学(355000) 郑一平

福建省宁德市第一中学(352100) 苏华春

命题者常喜欢把数列与相关知识综合作为高考压轴题考查学生数学解题能力和综合素质,是基于数列既是高中数学的主干知识,又是学习高等数学的基础,既具有函数的特征,又能构成独特的递推关系.从近年高考数列试题可以看出,由过去单纯考查数列知识或递推数列问题转化为在知识交汇上做文章,常以综合性问题形式作为压轴题出现.特别作为压轴题常设计了许多层次恰当、合理的综合性问题,使数列与高中阶段相关知识相结合,并以数列知识为载体注重考查数学推理能力和分析解决问题的能力,尤其考查学生对数学问题的理解水平和数学素养,成为学生数学高考得高分的关键.本文以浙江、北京、江苏近两年全国高考数列综合题为例,分析其三种新题型及其解题方法特点,对于做好数列教学与复习,尤其对提升数列综合题解题能力有很大帮助.

1 与不等式交汇的综合题

这类试题似乎考数列但又不单纯为数列,尤其注意在知识交汇上做文章,设计了层次恰当、合理的综合性问题,使数列与高中阶段重要的不等式等知识相结合, 考查不等式证明、计算的方法、技巧.

例1(2019年高考浙江卷)设等差数列{an}的前n项和为Sn,a3= 4,a4=S3, 数列{bn}满足: 对每n ∈N*,Sn+bn,Sn+1+bn,Sn+2+bn成等比数列.

(1)求数列{an},{bn}的通项公式;

(2)记Cn=证明:C1+C2+···+

分析(Ⅰ)首先求得数列{an}的首项和公差确定数列{an}的通项公式,然后结合三项成等比数列的充分必要条件整理计算即可确定数列{bn}的通项公式;

(Ⅱ)结合(Ⅰ)的结果对数列{cn}的通项公式进行放缩,然后利用不等式的性质和裂项求和的方法即可证得题中的不等式.

解析(Ⅰ)由题意得解得:故数列{an}的通项公式为an=2n-2.所以Sn=n(n-1).由n ∈N*,Sn+bn,Sn+1+bn,Sn+2+bn成等比数列知:

整理得:

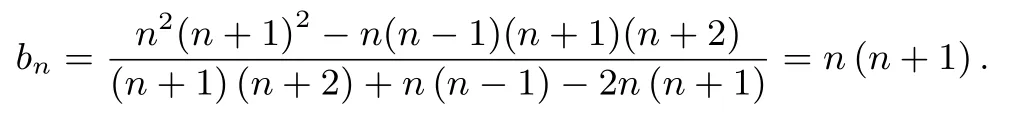
(Ⅱ)结合(Ⅰ)中的通项公式可得:

评析本题(Ⅰ)主要考查数列通项公式的求解,(Ⅱ)考查如何根据条件把等量关系转化为不等量关系,通过放缩方法结合裂项求和达到目的,意在考查学生的转化能力和计算求解能力.

例2(2020年高考浙江卷理科第20 题)已知数列{an},{bn},{cn}中,a1=b1=c1= 1,cn=an+1-an,cn+1=

(Ⅰ)若数列{bn}为等比数列,且公比q ＞0,且b1+b2=6b3,求q与{an}的通项公式;

(Ⅱ)若数列{bn}为等差数列, 且公差d ＞0, 证明:c1+c2+···+cn ＜1+

分析(Ⅰ)根据b1+b2=6b3,求得q,进而求得数列{cn}的通项公式,利用累加法求得数列{an}的通项公式.(ⅠⅠ)利用累乘法求得数列{cn}的表达式,结合裂项求和法证得不等式成立.

解(Ⅰ)依题意b1= 1,b2=q,b3=q2,而b1+b2= 6b3,即1+q=6q2,由于q ＞0,所以解得q=所以bn=因为bn+2=故cn+1=·cn= 4·cn,所以数列{cn}是首项为1, 公比为4 的等比数列, 所以cn= 4n-1.所以an+1- an=cn= 4n-1(n≥ 2,n ∈N*).所以an=a1+1+4+···+4n-2=

(ⅠⅠ)依题意设bn= 1+(n-1)d=dn+1-d, 由于(n≥2,n ∈N*),故

所以

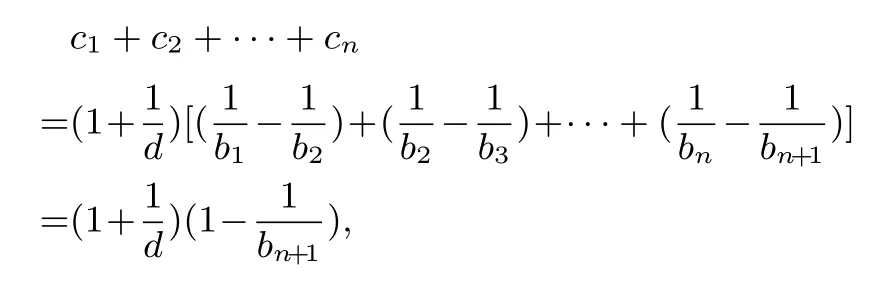
由于d ＞0,b1= 1, 所 以bn+1＞0, 所 以即c1+c2+···+cn ＜1+n ∈N*.

评析本题对能力要求较高,主要考查累加法、累乘法求数列的通项公式,考查裂项求和法和推理论证能力、分析问题和解决问题的能力.

2 新定义型数列综合题

新定义数列问题主要给出了数列新定义一种运算、概念(如一种符号、一种图形等)、一种性质等,由过去单纯考查数列知识或递推数列问题以及在知识交汇上做文章,变为设计层次恰当、合理的新问题,使数列与高中阶段相关知识相结合,并以数列知识为载体注重考查数学推理能力和分析解决问题的能力,要求学生在短时间内理解试题所给的新型定义,能将所学知识与方法迁移到不同情境中,进而考查学生的理性思维和数学素养.

例3(2019年高考江苏卷压轴题)定义首项为1 且公比为正数的等比数列为“M-数列”.

(Ⅰ)已知等比数列{an}满足:a2a4=a5,a3-4a2+4a1=0,求证: 数列{an}为“M-数列”;

(Ⅱ)已知数列{bn}满足:b1= 1,其中Sn为数列{bn}的前n项和.

①求数列{bn}的通项公式;

②设m为正整数,若存在“M-数列”{cn}(n ∈N*),对任意正整数k,当k≥m时,都有ck≤bk≤ck+1成立,求m的最大值.

分析(Ⅰ)只要求出数列{an}的通项公式即可判断结论;

(Ⅱ)①由题意利用递推关系式讨论推理可得数列{bn}是等差数列, 据此即可确定其通项公式; ②由①确定bk的值,将原问题进行等价转化,构造函数,结合导函数研究函数的性质即可求得m的最大值.

解析(Ⅰ)设等比数列{an}的公比为q,所以a1/=0,q /=0.由

因此数列{an}为“M-数列”.

②由①知,bk=k,k ∈N*.因为数列{cn}为“M-数列”,设公比为q,所以c1= 1,q ＞0.因为ck≤bk≤ck+1,所以qk-1≤k≤qk,其中k=1,2,3,...,m.当k=1 时,有q≥1;当k=2,3,...,m时,有

设f(x)=(x ＞1), 则f ′(x)=令f′(x)=0,得x=e.列表如下:

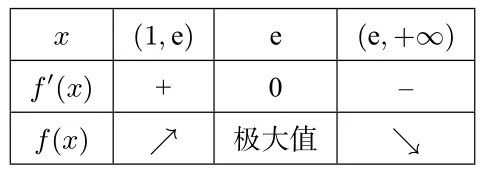
x (1,e)e (e,+∞)f′(x)+0-f(x)↗极大值↘

综上,所求m的最大值为5.

评析本题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力.尤其问题(Ⅱ)②要通过观察分析构作函数,把数列问题转化为函数问题利用导数知识来解决.

例4(2020年高考江苏卷第20 题)已知数列{an}(n ∈N*)的首项a1= 1,前n项和为Sn.设λ与k是常数,若对一切正整数n,均有成立,则称此数列为“λ-k”数列.

(Ⅰ)若等差数列{an}是“λ-1”数列,求λ的值;

(Ⅱ)若数列{an}是“-2”数列,且an ＞0,求数列{an}的通项公式;

(3)对于给定的λ, 是否存在三个不同的数列{an}为“λ-3”数列,且an≥0? 若存在,求λ的取值范围;若不存在,说明理由,

分析(Ⅰ)根据定义得Sn+1-Sn=λan+1,再根据和项与通项关系化简得an+1=λan+1,最后根据数列不为零数列得结果;

解(Ⅰ)Sn+1-Sn=λan+1,即an+1=λan+1,由a1=1,an+1/≡0,所以λ=1.

(Ⅱ)因为an ＞0,所以Sn+1＞Sn,所以因为所以所以Sn+1= 4Sn,所以Sn= 4n-1, 因为S1=a1= 1,Sn= 4n-1, 所以an= 4n-1-4n-2= 3·4n-2,n≥ 2, 所 以an=

(Ⅲ)假设存在三个不同的数列{an}为λ-3 数列.

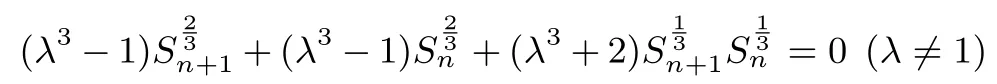
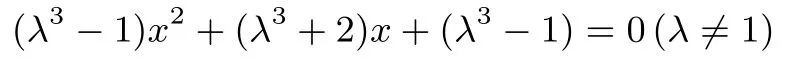
有两个不等正根,设f(x)=(λ3-1)x2+(λ3+2)x+(λ3-1)(λ/=1).

①当λ ＜1 时, Δ = (λ3+2)2-4(λ3-1)2＞0⇒0＜λ3＜4,即0＜λ ＜1,此时f(0)=λ3-1＜0,对称轴＞0,满足题意.

②当λ ＞1 时, Δ = (λ3+2)2-4(λ3-1)2＞0⇒0＜λ3＜4,即1＜λ ＜此时f(0)=λ3-1＞0,对称轴x=-＜0,此情况有两个不等负根,不满足题意舍去.

综上,0＜λ ＜1.

评析本题考查数列新定义、由和项求通项、一元二次方程实根分步以及综合分析求解能力,属难题.解决新定义问题的两个突破点: 一是正确理解新定义.耐心阅读, 分析含义,准确提取信息是解决这类问题的前提,剥去新定义、新法则、新运算的外表,利用所学的知识将陌生的性质转化为我们熟悉的性质,是解决这类问题的突破口.二是合理利用有关性质是破解新定义型问题的关键.在解题时要善于从题设条件给出的数式中发现可以使用性质的一些因素,并合理利用.问题(Ⅰ)比较简单;问题(Ⅱ)根据递推数列关系推导求得Sn= 4n-1,进而求得an达到求解目的;问题(Ⅲ)则通过变形、代换,把问题转化为一元二次方程根的分布问题,把数列问题转化为二次函数问题解决,意在考查学生的转化能力和推理能力.只有在分析条件理解题意的基础上,用所学知识进行推理方能奏效.

3.与数论相关的推理综合题

例5(2019年高考北京卷压轴题)已知数列{an},从中选取第i1项、第i2项、…、第in项(i1＜i2＜i3＜···＜in),若ai1＜ai2＜··· ＜aim,则称新数列ai1,ai2,··· ,aim为{an}的长度为m的递增子列.规定: 数列{an}的任意一项都是{an}的长度为1 的递增子列.

(Ⅰ)写出数列1,8,3,7,5,6,9 的一个长度为4 的递增子列;

(Ⅱ)已知数列{an}的长度为p的递增子列的末项的最小值为am0,长度为q的递增子列的末项的最小值为an0.若p ＜q,求证:am0＜an0;

(Ⅲ)设无穷数列{an}的各项均为正整数,且任意两项均不相等.若{an}的长度为s的递增子列末项的最小值为2s-1,且长度为s末项为2s-1 的递增子列恰有2s-1 个(s=1,2,···),求数列{an}的通项公式.

分析(Ⅰ)由题意结合新定义的知识给出一个满足题意的递增子列即可;(Ⅱ)利用数列的性质和递增子列的定义证明题中的结论即可;(Ⅲ)观察所要求解数列的特征给出一个满足题意的通项公式,然后证明通项公式满足题中所有的条件即可.

解析(Ⅰ)满足题意的一个长度为4 的递增子列为: 1,3,5,6.

(Ⅱ)对于每一个长度为q的递增子列a1,a2,··· ,aq,都能从其中找到若干个长度为p的递增子列a1,a2,··· ,ap,此时ap≤aq, 设所有长度为q的子列的末项分别为:{aq1,aq2,aq3,···}, 所有长度为p的子列的末项分别为:{ap1,ap2,ap3,···},则an0= mⅰn{aq1,aq2,aq3,···},注意到长度为p的子列可能无法进一步找到长度为q的子列, 故am0≤mⅰn{ap1,ap2,ap3,···},据此可得:am0＜an0.

(Ⅲ)满足题意的一个数列的通项公式可以是

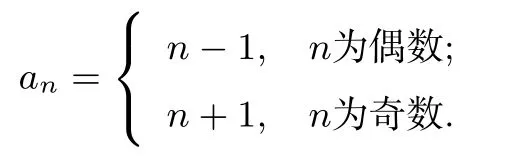
下面说明此数列满足题意.很明显数列为无穷数列, 且各项均为正整数, 任意两项均不相等.长度为s的递增子列末项的最小值为2s -1, 下面用数学归纳法证明长度为s末项为2s -1 的递增子列恰有2s-1个(s=1,2,···):当n= 1 时命题显然成立, 假设当n=k时命题成立, 即长度为k末项为2k -1 的递增子列恰有2k-1个,则当n=k+ 1 时, 对于n=k时得到的每一个子列as1,as2,··· ,ask―1,2k-1,可构造:as1,as2,··· ,ask―1,2k-1,2(k+1)-1 和as1,as2,··· ,ask―1,2k,2(k+1)-1 两个满足题意的递增子列,则长度为k+1 末项为2k+1 的递增子列恰有2×2k-1=2k=2(k+1)-1个.

综上可得,数列an==2,1,4,3,6,5,8,7 是一个满足题意的数列的通项公式.

评析本小题主要考查接受新知识能力,引入新定义,要求利用定义结合条件解决相关问题,所谓“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.特别问题(Ⅲ)对观察能力要求较高,观察得到通项后要求能利用数学归纳法进行证明有一定难度.

例6(2020年高考北京卷压轴题)已知{an}是无穷数列.给出两个性质:

①对于{an}中任意两项ai,aj(i ＞j),在{an}中都存在一项am,使

②对于{an}中任意项an(n≥3),在{an}中都存在两项ak,al(k ＞l).使得an=

(Ⅰ)若an=n(n=1,2,···),判断数列{an}是否满足性质①,说明理由;

(Ⅱ)若an= 2n-1(n= 1,2,···),判断数列{an}是否同时满足性质①和性质②,说明理由;

(Ⅲ)若{an}是递增数列,且同时满足性质①和性质②,证明:{an}为等比数列.

分析(Ⅰ)根据定义验证,即可判断;(Ⅱ)根据定义逐一验证,即可判断; (Ⅲ)首先,证明数列中的各项同号,然后证明a3=最后,用数学归纳法证明数列为等比数列即可.

解(Ⅰ)因为a2= 2,a3= 3,/∈Z,所以{an}不具有性质①;

(Ⅱ)因为∀i,j ∈N*,i ＞j,=2(2i-j)-1,2i-j ∈N*,所以=a2i-j.所以{an}具有性质①;因为∀n ∈N*,n≥3,∃k=n-1,l=n-2,= 2(2k-l)-1= 2n-1=an,所以{an}具有性质②;

(Ⅲ)首先, 证明数列中的各项同号, 不妨设已知某项是正数,往证数列各项恒为正数.显然an /= 0(n/∈N*),假设数列中存在负项,设N0= max{n|an ＜0},第一种情况: 若N0=1,即a1＜0＜a2＜a3＜···,由①可知: 存在m1,满足am1=＜0,存在m2,满足am2=＜0,由N0= 1可知从而a2=a3, 与数列的单调性矛盾, 假设不成立.第二种情况: 若N0≥2, 由①知存在实数m, 满足am=＜0,由N0的定义可知:m≤N0,另一方面,am==aN0,由数列单调性可知:m ＞N0,这与N0的定义矛盾,假设不成立.

同理可证得数列中若存在负数,则各项恒为负数.综上可得,数列中的各项同号.

其次, 证明a3=利用性质②: 取n= 3, 此时(k ＞l), 由数列的单调性可知ak ＞al ＞0, 而a3=ak ·＞ak, 故k ＜3, 此时必有k= 2,l= 1, 即a3=,最后,用数学归纳法证明数列为等比数列(过程留给读者).

综上可得,数列{an}的通项公式为:an=a1qn-1.即数列{an}为等比数列.

评析本题主要考查数列的综合运用,等比数列的证明,数列性质的应用,数学归纳法与推理方法、不等式的性质的综合运用等知识,意在考查学生的观察能力、转化能力和推理能力.问题(Ⅰ)与(Ⅱ)相对都比较简单, 问题(Ⅲ)对能力要求较高,关键突破点有三: 一要根据证明需要分情况逐一讨论;二要根据性质②找到前三项的等比关系;三要根据性质①找到数列中的其他项,并证明其他项依次满足等比关系.