利用切线解决最小距离问题的源与流

广东省中山市中山纪念中学 马红芳 李勇刚

在教学中,笔者发现一个问题: 很多同一个本质的问题改变了问题的呈现形式,学生就会觉得很困难,不会处理.如何解决这个问题? 笔者在教学中尝试通过变式教学去解决.首先引导学生掌握解决这类问题源问题的处理方法,然后通过变式,一方面让学生看到同样一个知识背景的不同呈现形式,学会透过不同的形式看到所研究问题的本质;另一方面通过变式层层深入,让学生对问题的本质有更深刻全面的认识,以期达到更好的教学效果.

本文首先是给出用切线解决直线和曲线上动点距离最小值问题的一个最基本的原型,通过一题多变,让学生看到很多看起来不同形式的问题,通过文字语言,图形语言以及数学符号语言的相互转化,可以化归为熟知的源问题.

例1已知点P在函数f(x)= ex的图像上运动,点Q在直线y=x上运动,求|PQ|的最小值.

解析对函数f(x)= ex的图像上的给定点P,点P与直线y=x上点的距离的最小值即点P到直线y=x的距离,故|PQ|的最小值即点P到直线y=x的最小距离.根据函数f(x)= ex的图像可知,把直线y=x平移到与函数f(x)= ex的图像相切时,切点到直线y=x的距离即是函数f(x)=ex的图像上的点到直线y=x的最小距离.

设切点坐标为(a,ea), 则该处切线的 斜 率f′(a)=f′(x)|x=a=ex|x=a= ea= 1, 所以a= 0, 故切点坐标为(0,1), 所以|PQ|mⅰn=

变式1已知点P在函数y=ex的图像上运动,点Q在函数y= lnx的图像上运动,求|PQ|的最小值.

图1

分析注意到函数y= ex与函数y= lnx互为反函数,故它们的图像关于直线y=x对称,故|PQ|的最小值即是函数y=ex的图像上的点到直线y=x最小距离的2 倍.

变式2已知点P在函数y=x2+1(x≥0)的图像上运动,点Q在函数y=的图像上运动,求|PQ|的最小值.

分析函数y=x2+1(x≥0)与函数互为反函数,故它们的图像关于直线y=x对称,所以|PQ|的最小值即是函数y=x2+1(x≥0)的图像上的点到直线y=x最小距离的2 倍.

变式3直线y=a与函数y=x2-lnx的图像和直线y=x-2 分别交于点P,Q,求|PQ|的最小值.

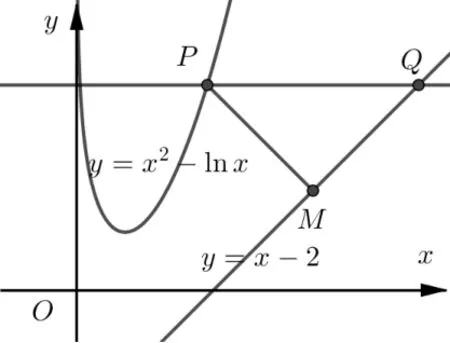
图2

分析先画出函数y=x2-lnx的图像, 以及直线y=x-2,y=a,则若要|PQ|小,则P点应取直线y=a与y=x2-lnx的图像右边的交点, 注意到y=a和直线y=x-2 总成45°角,|PQ|是水平距离,|PQ|和P到直线y=x-2 距离之比始终为定值故求|PQ|的最小值可转化为求函数y=x2-lnx的图像上的点和直线y=x-2上点距离的最小值,解决方法与例1 方法完全相同.

变式4已知实数a,b,c,d满足= 1,其中e 是自然对数的底数,求(a-c)2+(b-d)2的最小值.

分析= 1 即b=a-2ea,d= 2-c,故点P(a,b)是函数y=x-2ex图像上一点,点Q(c,d)是函数y=2-x图像上一点.因为(a-c)2+(b-d)2=|PQ|2,故问题实质上是求函数y=x-2ex图像上一点与直线y=2-x上一点距离的最小值,与例1 方法完全相同.

注这题是用数学符号语言表达点在曲线上、点在直线上、以及两点间的距离.

变式5若不等式(x-a)2+(x-lna)2＞m对任意的x ∈R,a ＞0 恒成立,求实数m的取值范围.

分析(x-a)2+(x-lna)2的几何意义是点(x,x)和点(a,lna)距离的平方, 点(x,x)在直线y=x上运动, 点(a,lna)在曲线y=lnx上运动,所以(x-a)2+(x-lna)2也表示直线y=x上的点和曲线y= lnx上的点的距离的平方,而(x-a)2+(x-lna)2＞m对任意的x ∈R,a ＞0恒成立,即[(x-a)2+(x-lna)2]mⅰn＞m,所以问题转化为求y=x上的点和曲线y=lnx上的点的距离的最小值.

变式6已知函数f(x)=(x-a)2+(lnx2-2a)2,其中x ＞0,a ∈R,若存在x0,使得f(x0)≤成立,求实数a的值.

分析(x-a)2+(lnx2-2a)2的几何意义是点(x,lnx2)和点(a,2a)距离的平方, 这题和上题的区别在于: 题目要求a的值, 说明点(a,2a)应该是个定点, 但这个定点在直线y= 2x上, 点(x,lnx2)(x ＞0)在曲线y= 2 lnx(x ＞0)上运动, 所以(x-a)2+(lnx2-2a)2表示直线y= 2x上的定点(a,2a)和曲线y=2 lnx上的点的距离的平方.

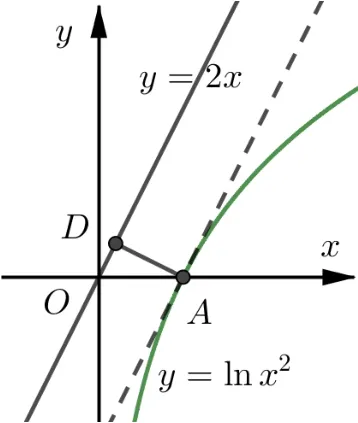
图3

存在x0＞0,使得f(x0)≤成立,即

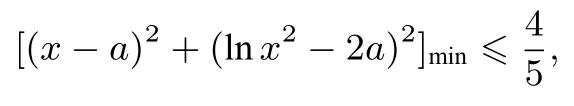
用例1 一样的方法,我们可以求出直线y= 2x上的点与曲线y=2 lnx上的点的距离的平方的最小值刚好是所以

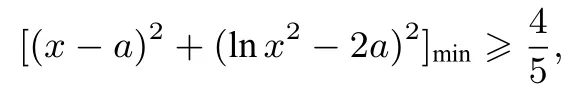
因 此[(x-a)2+(lnx2-2a)2]mⅰn=当且仅当点(x,lnx2)取如图所示的A点, 点(a,2a)为D(D为 过切点A作直线y= 2x垂线的垂足)点时, (x-a)2+于是只要求出A点坐标,利用kAD ×2 =-1 即可求出a的值.

利用切线求最小距离问题的最本源的问题是已知一条定直线和一个定曲线,求直线和曲线上两个动点距离的最小值.其方法是通过将直线平移,移到和曲线相切,切点到原来直线的距离即是直线上点和曲线上点的最小距离.这个问题的解决方法同学们是很容易掌握的,但是有些问题本质是用这个方法去解决,只是改变了题目条件或者所求目标的呈现形式,很多同学就不会处理.笔者认为产生这个问题的两个重要原因,一就是对问题的本质认识不够透彻,二是学生不善于把这些看起来陌生的问题转化为自己熟悉的知识点.从源问题出发,多角度多层次地变式,一方面让学生对这个问题涉及的知识点和方法有更深入的认识,另一方面也想引导学生在平时学习中要善于进行文字语言,图形语言,数学符号语言的转化,从而能快速的把所见到的问题与熟悉的问题相链接,用熟悉的方法去解决.培养学生对所学知识的迁移运用能力,提高思维品质.这样一种教学方法若要发挥出良好的效果,需要学生平时学习过程中打好扎实的基本功,教师教学的过程中要坚持渗透转化化归的思想.通过不断积累,学生对数学的理解也会逐渐清晰,从而走出困惑.