对2021年全国新高考数学Ⅰ卷第17题的研究

广州市教育研究院(510030) 陈镇民

一、引言

数列知识是刻画离散现象的数学模型.数列问题以其多变的形式和灵活的解题方法倍受高考命题者的青睐,是高考命题的“热点”.其中迭代法,累加法,待定系数法和数学归纳法是求递推数列通项公式的常用方法.高考中数列问题已逐步转向多元化,其命题形式多样,解题思路灵活.下面结合2021年全国新高考数学Ⅰ卷数学第17 题数列模型特点,探索出这类问题求解的一般方法并进行适当的拓展延伸,同时谈谈对我们中学数学教学的启示.

二、题目与解答赏析

题目(2021年新高考数学Ⅰ卷第17 题)已知数列{an}满足a1=1,an+1=

(1)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;

(2)求{an}前20 项的和.

(一)第(1)问解答赏析

本试题第(1)问的求解任务有两项: 首先是在已知条件下,对新定义的数列bn=a2n,要求先写出b1,b2的值(即特殊项);然后再求解数列{bn}的通项公式(即一般式).求解数列{bn}的通项公式一般有两种处理方法: 一是采用演绎推理方法;二是采用归纳—猜想—证明(数学归纳法)的方法.

解法1(演绎推理法): 由题设得b1=a2=a1+1 = 2,b2=a4=a3+1=(a2+2)+1=5.a2n+2=a2n+1+1=(a2n+2)+1=a2n+3.因为bn=a2n,所以bn+1=bn+3,即{bn}是以b1= 2 为首项, 公差为3 的等差数列.所以bn=2+3(n-1)=3n-1.

解法2(演绎推理法): 由题设得b1=a2=a1+1 = 2,b2=a4=a3+ 1 = (a2+2)+ 1 = 5.当n为偶数时,an+2=an+1+ 1 = (an+2)+ 1 =an+ 3, 所以an=

解法3(归纳—猜想—证明)由题设得b1=a2=a1+1 = 2,b2=a4=a3+1 = (a2+2)+1 = 2+3 = 5,b3=a6=a5+ 1 = (a4+2)+ 1 = 5 + 3 = 8.猜测bn=2+3(n-1)=3n-1.

下面用数学归纳法加以证明: ①当n= 1 时,b1= 2 =3×1-1, 显然成立.②假设当n=k(k≥1,k ∈N*)时成立,即bk= 3k-1.则当n=k+1 时,bk+1=a2k+2=a2k+1+1=(a2k+2)+1=a2k+3=bk+3=3(k+1)-1成立.所以bn=3n-1.

(二)第(2)问解答赏析

本试题第(2)问是求数列{an}的前20 项的和,一般有两种处理方法: 一是采用演绎推理的方法研究数列{an}的通项的特点然后再求和(解法1～解法3);二是采用完全归纳的方法把数列{an}的前20 项都求出来再求和(解法4).

解法1由(1)知a2n=3n-1,a2n-1=a2n-1=3n-2.所以{an}的前20 项和为

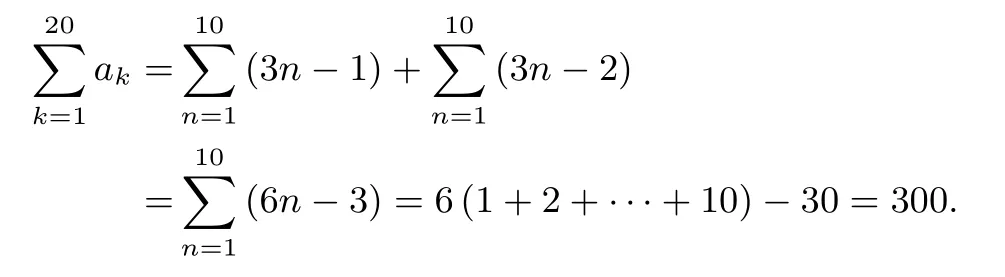
解法2由(1)知a2n=3n-1,a2n-1=a2n-1=3n-2.设{an}的前20 项和为S20,

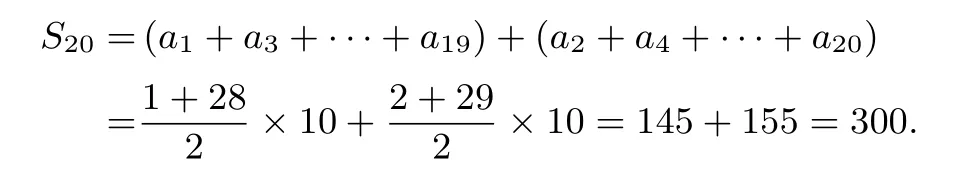
解法3由(1)知a2n=3n-1,a2n-1=a2n-1=3n-2,则a2n-1+a2n=6n-3.设{an}的前20 项和为S20,

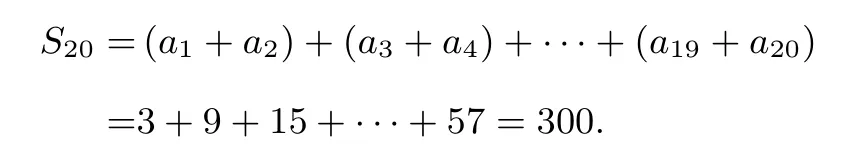
解法4a1=1,a3=4,a5=7,a7=10,a9=13,a11=16,a13= 19,a15= 22,a17= 25,a19= 28,a2= 2,a4=5,a6= 8,a8= 11,a10= 14,a12= 17,a14= 20,a16=23,a18=26,a20=29.设{an}的前20 项和为S20,

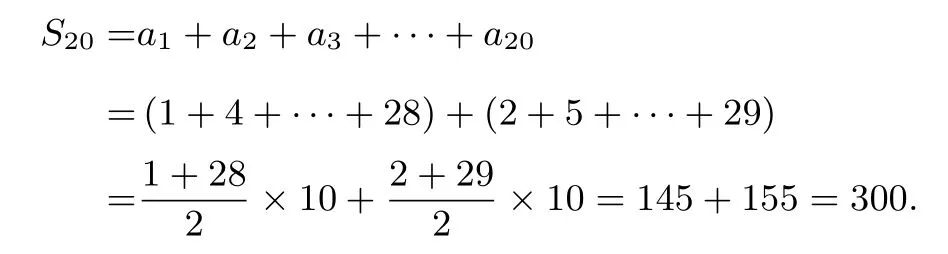
三、解题的新视角

对于本题所提供的数列递推模型,我们不禁要问: 能否把数列{an}的通项公式及其前n项和公式求解出来? 若能,本题的两个设问就可以一并解决.笔者提供一个解题的新视角,供读者参考.

由an+1=则

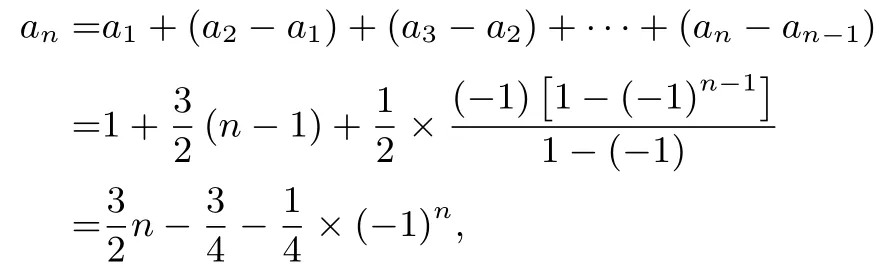
所以数列{an}的通项公式为an=×(-1)n,其前n项和

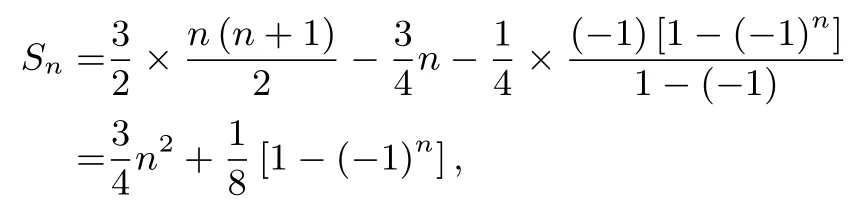
从而bn=a2n== 3n -1,S20=×(1-1)=300.

说明数列{(-1)n}是首项为-1,公比为-1 的等比数列.

四、试题的根源及拓展

鉴于文理不分卷,且第17 题是解答题的起点题,命题者充分考虑到让不同水平的考生可以获得不同的分数,因而设计了两问,且第(1)问先要求写出两个特殊项的值,然后再求通项公式,大大降低了试题的难度,让大部分考生可以获得一定的分数.命题者为了不落俗套,在已知条件中给出数列新的递推模型an+1

该模型的本质就是递推关系an+1=an+×(-1)n,这就是该模型的根与源.受新视角所提供的解法的启发,我们可以把试题进行适当地拓展延伸.

拓展1已知数列{an}满足a1=1,an+1=(p,q为常数,p/=0,q /=0).

求数列{an}的通项公式.

解由an+1=得an+1=an+×(-1)n, 即an+1-an=(-1)n.则

所以数列{an}的通项公式为

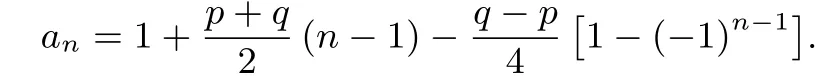
拓展2已知数列{an}满足an+1=求数列{an}的通项公式.

解由an+1=得an+1=×(-1)n,即an+1-an=n+×(-1)n.

则

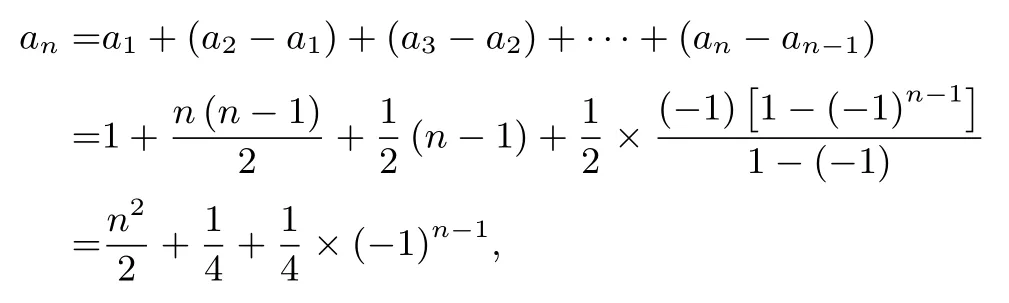
所以数列{an}的通项公式为an=×(-1)n-1.

拓展3已知数列{an}满足a1=1,an+1=求数列{an}的通项公式.

解由题设得an+1= 2an+×(-1)n, 即an+1+×(-1)n],则数列{是以a1+为首项,公比为2 的等比数列,所以an=×(-1)n.

进一步地,对于递推关系式为

an+1=(p为常数,且p/=0),或者

an+1=(p,s,t都为不等于0 的常数),同样可以求出数列{an}的通项公式,限于篇幅,留给读者去研究.

五、教学的启示

从阅卷结果可以看出, 大部分考生在第(1)问求数列的通项时错误类型多种多样, 导致零分率较高, 主要错因有: 第一是审题不周, 错误的求出b1=a2=a1+2 = 3,从而后面的求解都出错; 第二是概念的理解不到位, 如由b3-b2=b2-b1=3 或者由2b2=b1+b3,就下结论: 数列{bn}是等差数列;第三是没有熟练掌握在求解数列问题(特别是求递推数列的通项公式)时,可以适当考虑用“归纳—猜想—证明”的方法来解决问题.

针对评卷过程中发现的学生答题存在的问题,建议在教学中要注意做到以下几点.

1.加强对数学核心概念的教学.在概念教学中,应注意以下几点: 第一,提出概念的各种不同例子(正例)以促进概括;第二,举出不同的但和概念有关的例子(正例)帮助辨别;第三,提出不是概念的例子(反例)以促进辨别和概括;第四,设计运用概念解题情境, 提升对数学概念本质属性的理解,形成概念系统.

2.重视逻辑推理素养的达成.解题教学是逻辑推理素养达成的主要途径之一,在教学中,要重视学生解题教学活动的高参与度,引导学生通过解题活动加强对基础知识的巩固与系统掌握,提升逻辑推理能力.更重要的是教师要多让学生想(思维参与),不是仅告知学生怎么解,而是要引导学生通过对条件与结论的分析,探索论证的思路,选择合适的论证方法,让学生知道为什么要这样解;不要以解题方法多为出发点,而是要以为什么想到这个方法为落脚点.