化整式为分式 证明整式不等式

江西省共青城市国科共青城实验学校(332020) 姜坤崇

代数不等式从形式上大体可分为整式不等式、分式不等式及无理不等式等三类.整式不等式与分式不等式在证明中可以考虑互相转化,文献[1]阐述了将分式不等式转化为整式不等式的重要作用,而转化是相互的,因此对于某些整式不等式的证明,我们也可另辟蹊径,将其转化为分式不等式来证明,这种转化经常会收到意想不到的证明效果,下面分类举出数例说明之.

一、证明三元轮换对称不等式

在一个含有三元a,b,c的不等式中,若同时将a换成b,b换成c,c换成a且不等式不发生改变,则称这个不等式是关于a,b,c轮换对称不等式.显然,一个关于a,b,c对称的不等式(任意对调其中的两个字母不等式都不发生改变)的不等式一定是轮换对称不等式,反之则不然.对于许多关于a,b,c轮换对称的整式不等式化为分式不等式来证,可起到化繁为简、化难为易的效果.

例1已知a,b,c ＞0, 求证:a3b+b3c+c3a≥abc(a+b+c).

分析这个整式不等式从表面上看不难,但保持整式的形式进行证明却有一定困难,下面我们将其转化为分式不等式来证明可化难为易.

证明原不等式可化为

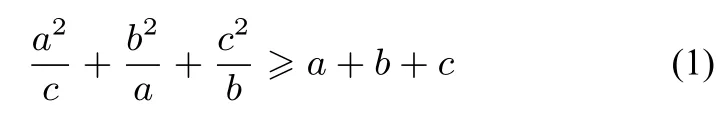
说明例1 也可以采用下面的方法来证明: 由7 元均值不等式得a3b+a3b+a3b+a3b+b3c+c3a+c3a≥= 7a2bc, 即4a3b+b3c+2c3a≥7a2bc, 同理,4b3c+c3a+2a3b≥7b2ca,4c3a+a3b+2b3c≥7c2ab,以上三个不等式相加得7(a3b+b3c+c3a)≥7(a2bc+ab2c+abc2),即a3b+b3c+c3a≥abc(a+b+c).

显然,以上证明是不简单也不易一下子想到的(为什么用7 元均值不等式? ),两种证法比较,化为分式证明的方法要简单得多.

有了对例1 解决问题方法的指引,以下例2、3、4、5 的解决就变得轻松多了.

例2(自编题)设a,b,c ＞0,求证:a3b2+b3c2+c3a2≥abc(ab+bc+ca).

证明将所证不等式化为分式不等式得

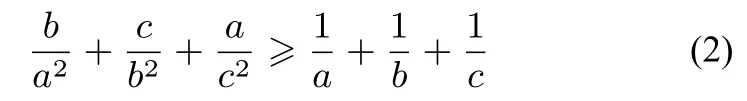
例3(自编题)设x,y,z是正实数,求证:x3y2(y+z)+y3z2(z+x)+z3x2(x+y)≥2xyz(xy2+yz2+zx2).

证明将所证不等式化为分式不等式得

例4(自编题)已知a,b,c ＞0,求证:a5b2+b5c2+c5a2≥a2b2c2(a+b+c).

证明原不等式可化为)

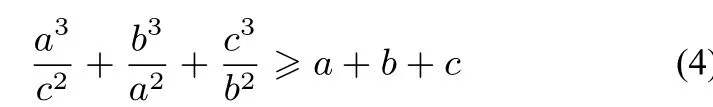
例5(自编题)已知a,b,c ＞0,求证:a8b3+b8c3+c8a3≥a3b3c3(a2+b2+c2).

证明原不等式可化为

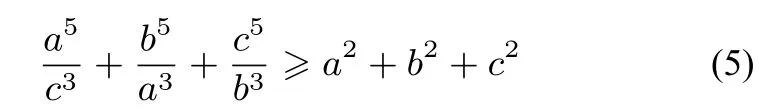
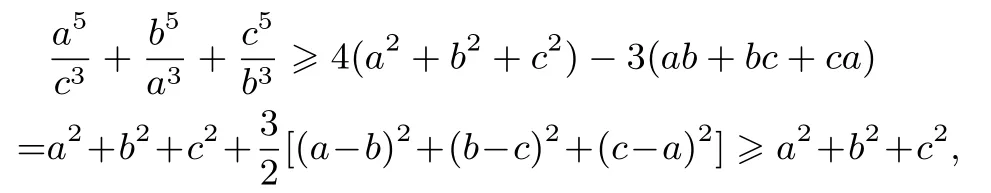
即(5)式成立,从而原不等式得证.

二、证明二元三元对称不等式

例6已知x、y、z是正实数,求证:

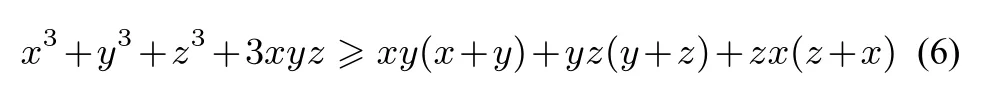
证明将不等式(6)等价转化为一分式不等式得

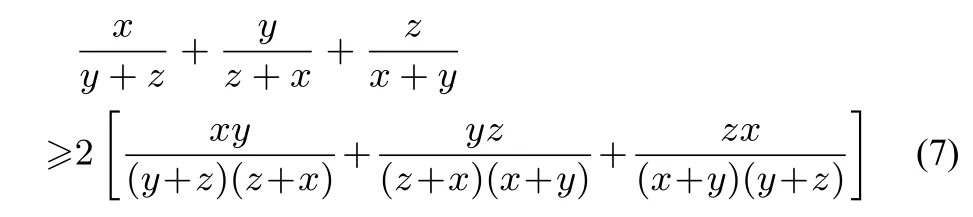
由二元均值不等式得

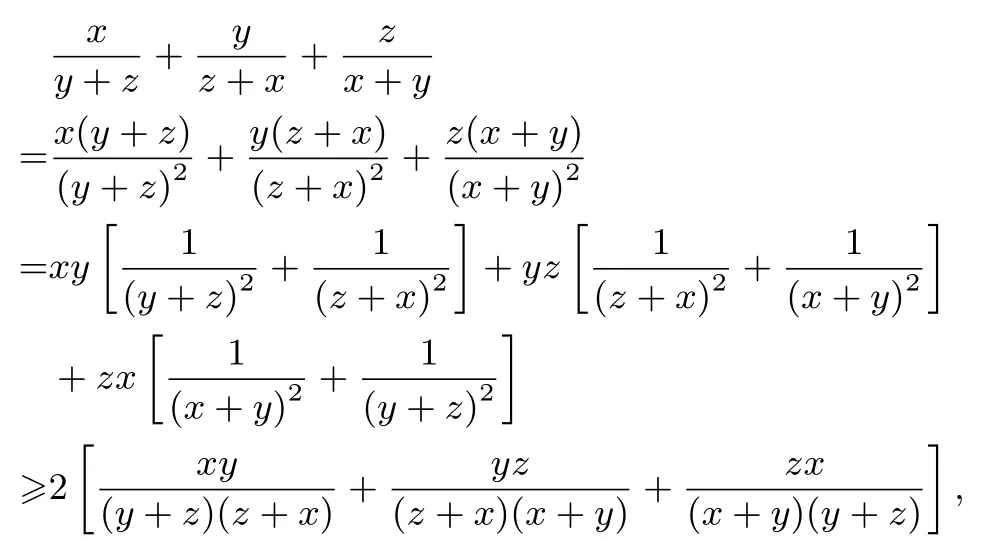
即(7)式成立,从而(6)式得证.

说明不等式(6)即著名的舒尔不等式:xr(x-y)(xz)+yr(y-z)(y-x)+zr(z-x)(z-y)≥0(其中x、y、z、r ＞0)当r= 1 时的一种等价形式,以上提供了一种证明舒尔不等式的新方法.

例7(自编题)设a,b,c ＞0, 求证:a2b2(a+b)4+b2c2(b+c)4+c2a2(c+a)4≥16a2b2c2(a2+b2+c2).

证明将不等式化为分式不等式得

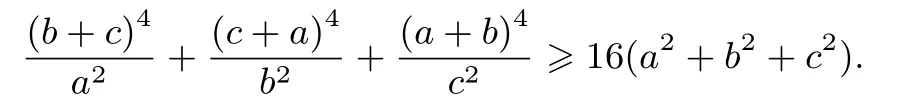
由三元均值不等式得

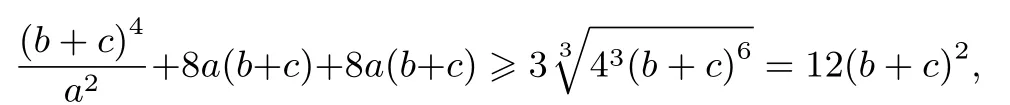
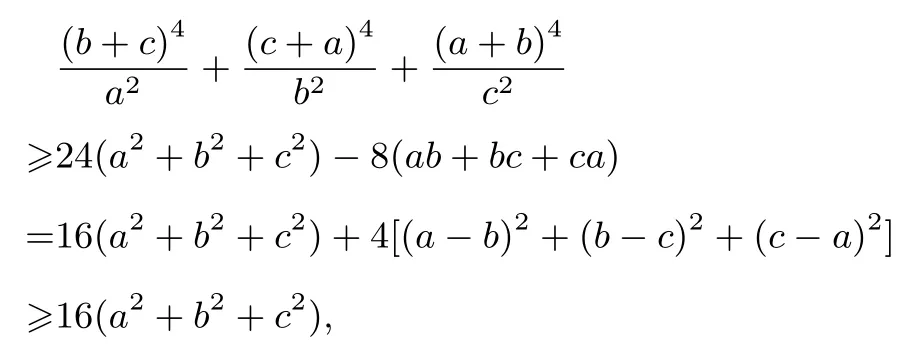
例8(自编题)设a ＞1,b ＞1,求证:a3+b3+8(a+b)≥a2+b2+8ab+8.

分析这个不等式直接证明不好证,而转化为分式不等式证明则容易进行.

证明因为a ＞1,b ＞1,所以

由二元均值不等式得

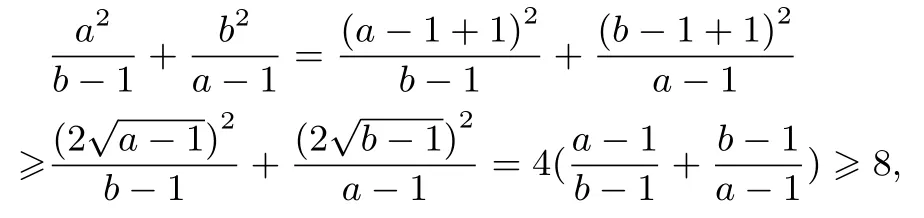
当且仅当a=b=2 时等号成立,所以原不等式成立.

说明不等式(8)为第26 届独联体数学奥林匹克竞赛题: 证明: 对任意a ＞1,b ＞1,有不等式≥8.

例9(自编题)设a ＞1,b ＞1,求证: 2(a4+b4)+27(a+b)≥2(a3+b3)+27ab+27.

证明因为a ＞1,b ＞1,所以

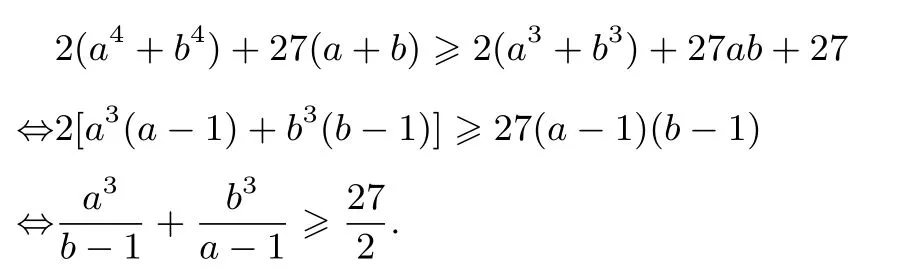
由二、三元均值不等式得

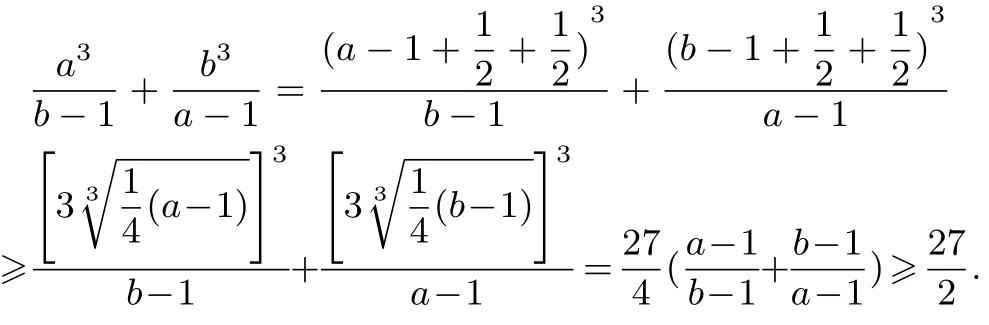
当且仅当a=b=时等号成立,所以原不等式成立.

例10(自 编 题)设a,b,c ＞0, 求证: (ab+bc+ca)[(a+b)2+(b+c)2+(c+a)2]≥12abc(a+b+c).

证明不等式可化为

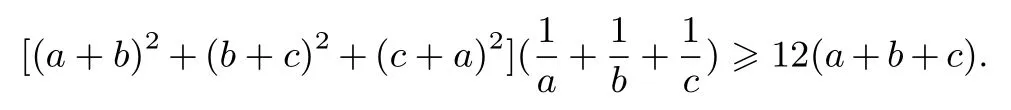
三、证明条件不等式

例11(自编题)已知实数a ＞1,b ＞1,c ＞1, 且a2+b2+c2=9,求证:a3+b3+c3≥

证明由a ＞1 得a-1＞0,a2-1＞0,由三元均值不等式得

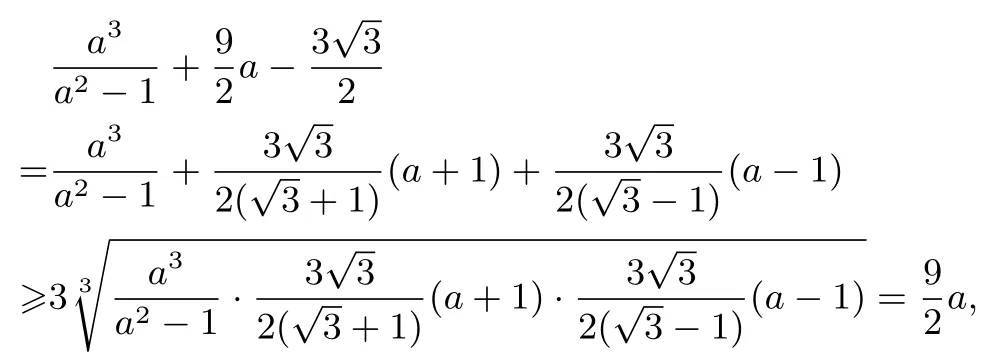
例12(自编题)已知实数a ＞1,b ＞1,c ＞1, 且a2+b2+c2=5,求证:a5+b5+c5≥

证明由a ＞1 得a-1＞0,a2-1＞0,由五元均值不等式得

当且仅当a=时上式等号成立.所以即同理,

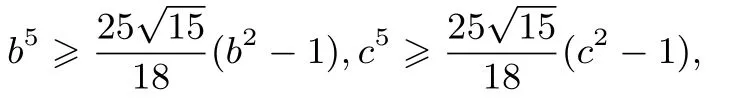
以上三式相加得

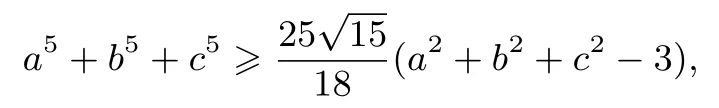
即a5+b5+c5≥

四、证明多元对称不等式

例13(自编题)已知λ为正实数,xi ＞ λ(i=1,2,··· ,n,n≥3),k为整数,且k≥n,求证:

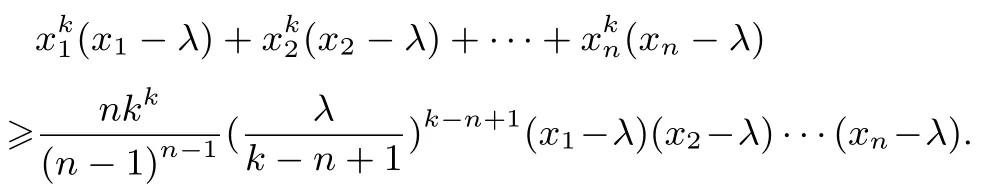
证明原不等式可化为

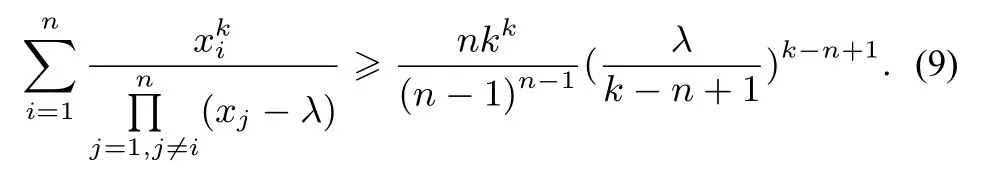
记Ai=

则由k元均值不等式得:

即

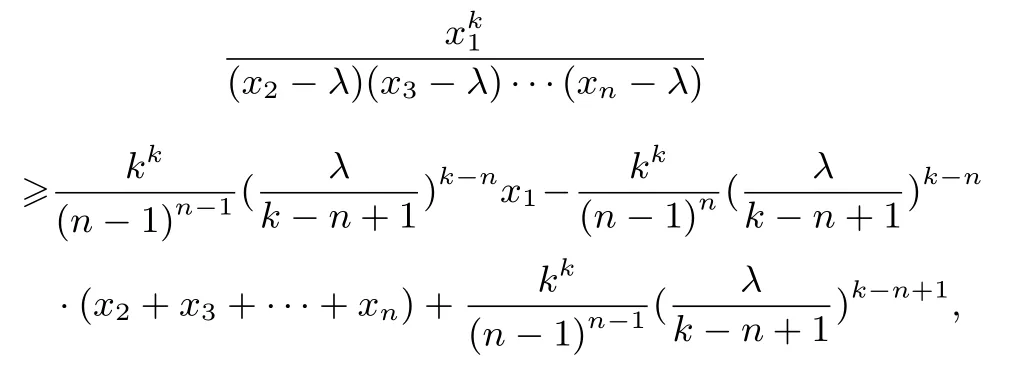
同理可证,

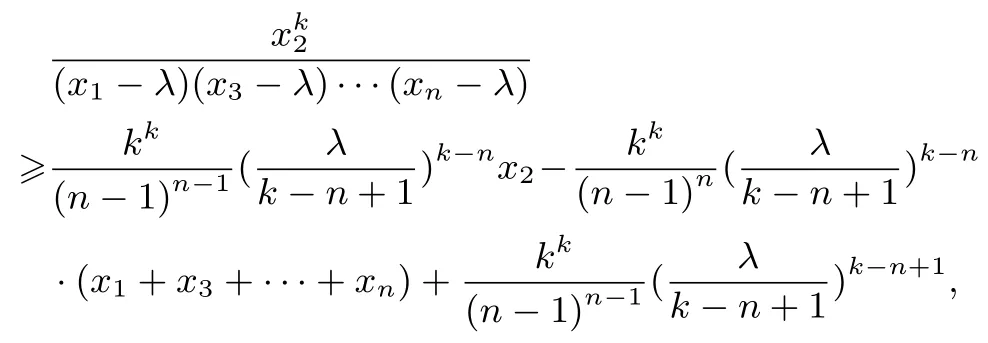
以上n个不等式相加即得不等式(9).

从以上的证明可以看出, 当且仅当xi=(i= 1,2,··· ,n)时所证不等式等号成立.所以原不等式成立.