凸显核心概念 彰显素养目标*——2019年甘肃省中考数学卷第28题解析与思考

甘肃省甘州区思源实验学校(734000)李永明

《普通高中数学课程标准(2017年版)》明确提出了发展学生数学核心素养的课程目标,综观全国近几年的中考压轴题,都能把知识技能、数学思考、问题解决和情感态度等方面全面的考查,凸显核心概念 彰显素养目标.2019年甘肃省中考数学卷第28题以创新引领,紧扣基础、层次分明、数形互动,立足模式,解法多元,彰显思想为特征,在每个维度都能有机融合,逐步实现由知识立意向能力立意转变,由能力立意向素养立意实现,体现了考查学生感悟、意识、思想、能力等数学核心素养的意图,达到提升学生数学核心素养的目的.

1 试题呈现

2019年甘肃中考第28 题如图1,抛物线y=ax2+bx+4 交x轴于A(-3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P的横坐标为m.

图1

(1)求此抛物线的表达式;

(2)过点P作PM ⊥x轴,垂足为点M,PM交BC于点Q.试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标,若不存在,请说明理由;

(3)过点P作PN ⊥BC,垂足为点N.请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?

2 试题解读

本题是甘肃卷简答题的压轴题,试题围绕抛物线的表达式、点的存在性、最大值等热点问题进行综合设计,其中蕴含了丰富的数学思想和方法,有分类讨论、方程思想、模型思想、转换思想等,这些都能有效地考查学生的核心素养.

2.1 紧扣教材,方法多样,凸显核心概念

核心概念本质上体现了数学的基本思想,是数学课程的目标点.试题紧扣教材,遵循历年的考查方向,以平面直角坐标系为背景,结合等腰三角形、直角三角形、一次函数的图象、二次函数的图象等基本图形,主要考查了二次函数的表达式、一次函数、二次函数与基本几何图形结合的综合能力,每一问梯度明显,层次分明,真正体现了所有学生在本题中都有不同的收获.第(1)问源于北师大版教材九年级下册的“3 确定二次函数的表达式”,一般采用待定系数法、交点式、顶点式等多种方法解答;第(2)问源于北师大版八年级下册的“等腰三角形”,一边为底、腰分三种情况进行分类讨论,并利用勾股定理、一次函数、方程、方程组等来解决;第(3)问源于北师大版教材九年级下册的“4 二次函数的应用”求最值的问题,可应用顶点式法、交点法、点到直线的距离公式等方法来解决.这三问都紧密结合教材中的核心知识点,采用多种不同的解题方法,从不同层次来考查学生的综合能力,凸显了核心知识的综合应用.

2.2 提炼模型,分类讨论,培养应用意识

模型思想是10 个核心概念中唯一以“思想”指称的概念.第(1)问灵活的设计了抛物线与x轴的两个交点和抛物线的表达式,能让学生从题目中提炼出抛物线的表达式这个数学模型,用通用方法待定系数法求出抛物线的表达式,学生也可以用交点式等方法求出抛物线的表达式,充分体现了数学基本特性;第(2)问学生提炼等腰三角形模型,固定一条边为底,其它两条边为腰,分三种情况进行分类讨论,逐步渗透了代数式、方程、一次函数、方程组、基本图形等数学模型;第(3)问以“最大值问题”为背景,渗透点的坐标、代数式、直角三角形、三角函数、一次函数、二次函数等数学模型,培养了学生的应用意识和创新意识.

2.3 理解抽象,化动为静,提升核心素养

化动为静是理解抽象问题的重要方法.命题人设计的第(2)问点的存在性问题,第(3)问最值问题这些都是比较抽象的数学问题,也是最能体现符号意识、运算能力、推理能力、模型思想等核心概念.第(2)问探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形,解决这一类问题,首先假设线段BC上存在这个点,画出示意图形,根据图形中线段的等量关系,然后通过勾股定理列方程求解,动点问题就转化成了方程解的存在性问题;第(3)问用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,根据函数表达式设点P和点Q的坐标,化动为静,然后表示出线段PQ的长度,用三角函数就可以表示出线段PN的长度,即关于未知数m的一个二次三项式,通过配二次函数的顶点式就可以求出最大值,提升了学生的核心素养.

3 解法赏析

关于第(1)问:

解法1:待定系数法

图2

图3

图4

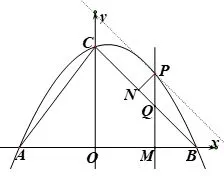
图5

四、教学思考

4.1 回归教材,加强核心概念教学

注重知识的来龙去脉,加强核心内容的教学,要让所有的数学知识回归教材.即教学中要让学生知道题目中的数学知识“从哪里来”,“又会到哪里去”,哪些是核心知识,又该如何复习等.第(1)问求此抛物线的表达式,问题源于北师大版教材九年级下册的“3 确定二次函数的表达式”,这是一个基础性的必考题,一般采用待定系数法、交点式、顶点式等多种方法,分析清楚所有问题以后,教师可以引导学生结合课本重点例题、习题复习待定系数法、交点式、顶点式等核心内容,回归教材知道这些知识点的来源出处,真正起到画龙点睛的作用.

4.2 关注模型,强化数学模型教学

数学建模是通过建立模型的方法来求得问题解决的思维活动过程,一般要经历“问题情境——问题模型——求解验证”三个过程,教学中教师要紧密结合实际,引导学生运用函数、方程、方程组、几何图形等数学模型,把它们多方位的渗透,逐步培养学生的数学模型思想.第(2)问中线段AC固定,点Q为动点,要求点Q的坐标,必须先要化动为静固定点Q的位置,进而假设出线段AC可以是等腰三角形的底或腰,这是一个抽象的建模过程,为了验证点Q的存在性,再利用方程检验其真假.这些环节中都需要教师在教学中逐步渗透和引导学生不断感悟,在每个教学环节中逐步渗透模型思想,从相对简单到相对复杂,从相对具体到相对抽象,让学生逐步积累活动经验,掌握数学建模方法,逐步形成运用数学模型去进行数学思考的习惯,培养学生的核心素养.

4.3 训练思维,加强几何直观教学

数学是思维的体操,教数学一定要“教”思维.教思维要以基本的数学图形为载体,学生“借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果.”教学过程当中,教师让学生识图、画图,逐步养成看图、画图的好习惯,并鼓励从图形中“质疑——发现和提出问题”,学会从“数”和“形”两个方面认识数学.第(3)问的教学中要充分利用图形进行分析,尽量把问题变的直观,直观了就容易展开形象思维,建立数学模型.所以,一定要加强几何图形的教学,将相对抽象的思考对象“图形化”,从“形”的方面感知数学,从“数”的方面解决问题,培养学生的创新意识.