改进的粒子群算法在太阳能光伏发电资料同化中的应用研究
李君妍,童亚拉
(1.湖北第二师范学院计算机学院,武汉 430205;2.基础教育信息技术服务湖北省协同创新中心,武汉 430205;3.湖北工业大学理学院,武汉 430068)
近年来,随着太阳能作为新能源带动光伏发电被广泛应用,质量高的光伏发电预测成为了一种需求[1-2],资料同化是数值预报模式提供高质量初值的方法,其中变分同化问题是一个非线性最优化问题,由于计算量太大、模式复杂及同化结果依赖于初猜值的选取,对于算法的收敛性、精确性均有很高的要求[3-4].国内外学者们为解决此问题做了大量研究工作,其中最有代表性的是Tao Sun等设计的多时标的四维变分数据同化方案[5],Tian等设计的非线性最小二乘四维变分数据同化方法[6],Rossella Arcucci采用截断奇异值分解方案和Tikhonov正则化方法[7-8],以及吴祝慧等设计的基于区域逐步分析的同化方法[9].然而,粒子群在特定同化过程中所达到的精度及速度还远远不够,这也是大多数智能优化算法在资料同化的应用上研究解决的重点.
鉴于PSO存在过早收敛或陷入局部极优的问题,刘晓彦等引入“早熟”判断机制,对粒子更新后的位置进行混沌扰动,避免陷入局部最优[10],但算法速度有待提高;王晨思等提出了一种权重寻优的粒子群算法,通过动态自适应方式对惯性权重进行更新,提高了算法的精度而算法时间没有改善[11];徐星等将热力学原理和热运动机制引入到粒子群优化算法中,提出了一种基于分子动理论的粒子群优化算法(MMT-PSO),大大提高了算法的精度[12],但在处理大数据问题时算法速度较慢.郑琴通过改进权重下降策略以及学习因子,提出了一种动态惯性权重PSO算法以求解含不连续开关过程的变分资料同化问题.与GA同化方案和伴随方法相比,数值试验结果显示:PSO方案的同化结果质量远高于前两种方案,鲁棒性也更强,但由于粒子个数的有效设置较差,完成同化所耗费的时间远大于伴随方法[13].张成兴提出结合时变加速因子的粒子群算法,通过时变的加速因子,较好平衡了粒子群算法的全局和局部搜索模型,但算法速度提高不大[14].受上述启发,本文设计了一种新的分子运动粒子群算法——并行分子运动论粒子群优化算法(PMPSO),其基本思想是将粒子群分成N个子集(N不大于CPU的核数),每个子集同时进行粒子迭代运算,以提高算法处理速度;每次迭代完后将每一子集中的头号精英粒子数据传递给公共部分,再进行下一次迭代,这样,既提高了算法处理速度又不降低进化精度.将PMPSO用于资料同化过程[15-16],与动态权重粒子群算法PSOCIWAC和时变双重压缩因子粒子群算法PSOTVCF相比,实验结果表明PMPSO在上时间、精度上具有很大的优势.
1 资料同化控制方程
本文里的资料同化控制方程来源于文献[17]中的偏微分方程:
(1)
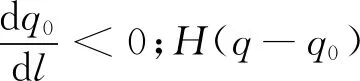
(2)
模拟参数化过程中的“on-off”开关.相应于(1)的数值模式为:
(3)
其中,Δl表示空间步长,li=iΔl,i为空间格点;Δt表示时间步长,tk=kΔt,k为空间层.N=T/Δt为积分过程中总的时间层;M+1=(T/Δt)+1为空间离散点总数.
2 基于分子运动论的粒子群算法
本算法中的粒子属性包括速度和位置以及加速度.此外,借鉴统计物理学和热力学中的质心和加速度的概念,定义了群质心和加速度.
群质心计算公式如下:
(4)
其中,Xi为种群内第i个粒子的坐标;mi表示中第i个粒子的质量,可视mi为粒子i的权重,实际处理时将mi视为粒子i的适应值,不妨假设粒子质量均为1,式(4)可简化为
(5)
当F在斥力和引力之间转换时,F的大小和方向随分子间距离变化而变化,根据牛顿第二定律
(6)
加速度a的大小和方向也随之变化.若不计加速度大小变化,当分子力为引力时a=1,为斥力时a=-1.
综上所述,粒子的速度更新公式变更为
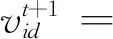
(7)
式中,ai为粒子i的加速度.初始化时粒子的加速度设置1,迭代过程中,粒子i与群质心间的距离d(Xcen,Xi)时刻调整[12].
融合了分子运动论的PSO算法在精度上得到了提高,这是因为算法把种群中每个粒子类比成分子,由于粒子和质心间的距离不同,粒子与质心间的分子作用力控制粒子的飞行方向,决定了粒子是向着质心还是背着质心的方向飞行.当d(Xcen,Xi)小于某个阈值d1时,分子作用力为斥力,此时粒子远离质心,种群多样性得以保持,全局搜索能力增强;当d(Xcen,Xi)小于某个阈值d2时,分子作用力为引力,此时粒子飞向质心,算法收敛性得以保持,局部搜索能力增强,这种机制有效增加了种群多样性,从而平衡全局和局部搜索[12].
3 资料同化中的分子运动论粒子群算法
3.1 适应度函数计算
PSO中个体根据适应度的高低进行评价,当个体适应度越高,则离目标函数最优解越近;当个体适应度越低,则离目标函数最优解越远,即适应度高的状态应该对应目标函数的较优状态.由于变分同化是最小化问题,于是将上述基于分子运动论的粒子群算法运用到变分同化问题之中求解变分同化代价函数的最小值.
资料同化代价函数定义如下:
(8)
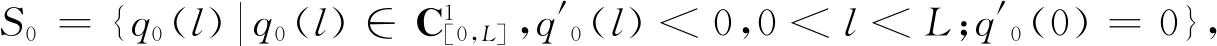
相应式(4)的离散代价函数为
(9)
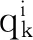
定义PSO中的适应度函数为:
(10)
其中,
3.2 基本流程
将基于分子运动论的粒子群算法应用于变分资料同化的计算流程如下:
1)初始化种群粒子.初始化粒子的位置、速度和加速度,确定最大迭代次数;
3)更新粒子的pbest和gbest.重新计算每一个粒子的适应度值,并将其与粒子的最优位置比较,从而更新粒子的pbest,再比较当前所有的pbest和gbest,以更新gbest;
4)如果达到最大迭代次数,执行7),否则执行5);
5)计算每个粒子距离种群重心的距离,若距离重心超过最远距离则加速度为正,反之加速度为负;
6)通过公式(9)和(5)调整粒子的速度与位置,然后执行2);
7)输出全局最优解,算法结束.
4 并行分子运动论粒子群算法(PMPSO)在资料同化中的应用
针对标准粒子群算法在精度上的不足,基于分子运动论的粒子群算法在此基础上进行了改进,但在同化时间即算法速度上却得不到提升.本文采用并行计算的原理对分子运动论粒子群算法加以改进.并行计算的基本思想是将粒子群分成N个子集(N不大于CPU的核数),每个子集交给一个线程控制,同时进行粒子迭代运算,以提高算法处理速度;每一子集中的头号精英粒子,将数据传递给公共部分在每次迭代完后,然后进入下一次迭代,其目的是让每个子集间进行信息交流以增加多样性.采用这种方式增加多样性是因为以异步通信形式进行并行运算可有效避免精度下降的同时,实现信息交流;另外,由于并行算法的本质是最大限度的提高硬件的利用率,算法结果依旧能保持良好的精度.
基于PMPSO算法的资料同化计算流程如下:
1)初始化种群粒子.初始化粒子的位置、速度和加速度,确定最大迭代次数;
2)将粒子随机分成N个种群,并分配给计算机的N个核;
4)更新粒子的pbest和gbest.重新计算每一个粒子的适应度值,并将其与粒子的最优位置比较,从而更新粒子的pbest,再比较当前所有的pbest和gbest,以更新gbest;
5)如果达到最大迭代次数,执行8),否则执行6);
6)计算每个粒子距离种群重心的距离,若距离重心超过最远距离则加速度为正,反之加速度为负;
7)通过公式(9)和(5)调整粒子的速度与位置,将四个种群的全局最优和个体最优比较留下最好的,然后执行3);
8)输出全局最优解,算法结束.
5 数值实验结果分析
5.1 仿真环境
借用文献[13]和文献[14]的实验数据和实验分析方法,将时变双重压缩因子粒子群算法(PSOTVCF)、动态权重粒子群算法(PSOCIWAC)和本算法(PMPSO)分别应用于变分资料同化,进行研究精度和时间上的比较.其中,后两种算法中的惯性权重从0.7线性递减到0.1;PSOTVCF的加速度因子:第一个压缩因子为常量,C1=2.6,C2=1.2;第二个压缩因子呈时变状态,C1N=2.88,C1M=2.68,C2N=2.45,C2M=1.25,PSOCIWAC和PMPSO的加速度因子:C1=2.6,C2=1.2;d1,d2分别设置为0.01和0.4.初始化200个粒子进行1 000次迭代;测试环境为硬件Intel Core i5,软件MATLAB R2017a.
5.2 收敛精度
图1是200次迭代同化后收敛精度的比较.图中,所划出的横线分别表示3种实验迭代次数为200时1 000次同化试验的平均值,横坐标表示迭代次数,纵坐标表示收敛精度的对数log10J,越小代表同化后的初值越接近观测值,从图中可以看出PMPSO算法精度明显高于PSOCIWAC算法和PSOTVCF算法.
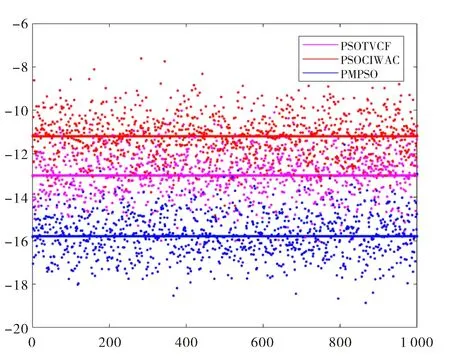
图1 200次同化(Iter=200)后收敛精度比较Fig.1 The convergence accuracy comparison after 200 times iteration
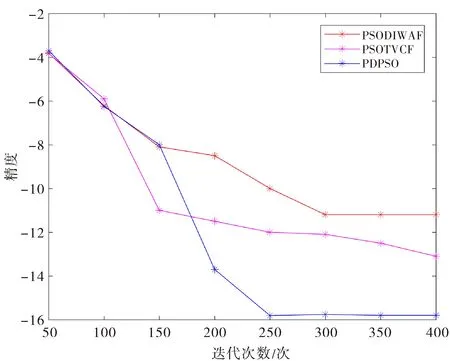
图2 收敛精度变化趋势图Fig.2 The convergence accuracy change tendency
图2展示了3种算法随迭代次数增加所对应的收敛精度变化趋势图.图中横坐标表示以每隔50代取一次的方法记录种群精度的次数,纵坐标表示收敛精度的对数log10J.观察图1可知,当迭代次数达到100代,3种方法收敛精度变化大致相同;当迭代次数达到150代,PSOTVCF显示出较大优势,同化质量远超PSOCIWAC和PMPSO,但仍有粒子尚未收敛;当迭代次数达到200代,PSOTVCF和PSOCIWAC图像趋于平衡状态,表示两种算法皆已基本收敛,而PMPSO还处于未完全收敛的状态,此时PMPSO收敛精度已经远超其余两种算法.当迭代次数达到400次时,PSOCIWAC收敛到-11.2,PSOTVCF收敛到-13,PMPSO收敛到-15.8.可知PMPSO同化结果的质量远高于PSOTVCF和PSOCIWAC,这是因为算法把种群中每个粒子类比成分子,由于粒子和质心间的距离不同,粒子与质心间的分子作用力控制粒子的飞行方向,决定了粒子是向着质心还是背着质心的方向飞行.分子作用力为斥力,此时粒子远离质心,种群多样性得以保持,全局搜索能力增强;分子作用力为引力,此时粒子飞向质心,算法收敛性得以保持,局部搜索能力增强.这使得种群的多样性得以协调,算法能够平衡全局搜索和局部搜索.
5.3 同化时间
表1展示了不同迭代次数所对应耗费的同化时间,每种迭代次数进行4次同化实验,下表取其平均值进行展示.
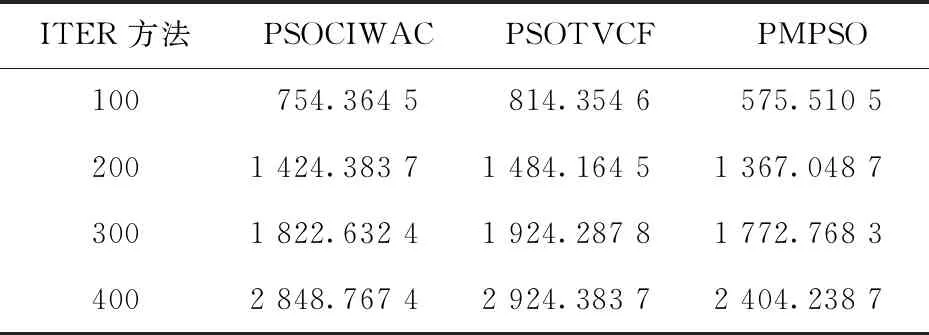
表1 同化耗费时间表Tab.1 Assimilation time table
由表可知,PMPSO在不同迭代次数所对应耗费的同化时间最短,这是因为PMPSO运用多核CPU的计算方式,将粒子群分为四个粒子群子集,再把每个子集代入一个核进行计算,由此大大缩短了同化时间.综上所述,PMPSO在同化时间上相对于其他三种算法得到了提升,具有一定的优越性.
6 结语
针对分子运动论PSO算法在处理大数据时速度较慢的问题,本文着重并行计算思想改进了算法,最大限度的提高计算机硬件以提高算法运行速度,在种群更新策略上,每一子集中的头号精英粒子,将数据传递给公共部分在每次迭代完后,然后进入下一次迭代,以保证多样性.将所设计的算法应用于变分资料同化中,与动态权重PSO算法和双重时变压缩因子PSO算法相比,在收敛精度和同化时间上有了较大的提升.同时,本文仅将算法应用于含“开关”过程的变分资料同化中,后续可尝试着将PMPSO应用于其他场景下的资料同化,扩大所设计算法的适用空间.

