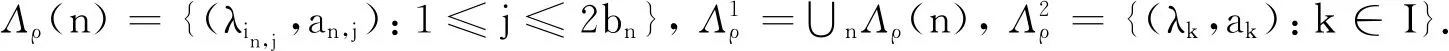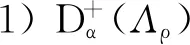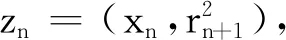框架谱Beurling维数和密度的连续性
刘 春 苔
(武汉轻工大学数学与计算机学院,武汉 430023)
指数型框架,亦称为Fourier框架[1-2],具有广泛的应用[1-3],其定义如下.
定义1设μ是d中有限Borel测度,Λ是可数集.若函数族{e2πi〈λ,x〉:λ∈Λ}是L2(μ)中的框架,则称μ是L2(μ)的Fourier框架谱测度,且称Λ为测度μ的一个Fourier框架谱.特别的,若E(Λ)为L2(μ)的正交基,则称μ为谱测度,且称Λ为μ的一个谱.
为行文方便,Fourier框架谱测度和Fourier框架谱分别简称为框架谱测度和框架谱.如何确定一个测度是否为框架谱测度(或谱测度)是一个非常吸引人的问题,已经涌现大量结果(参见文献[3-10]及它们所提及的文献),本文关心框架谱测度和谱测度的另一个问题:确定框架谱或谱的结构.对于此问题,常用的工具是Beurling密度和Beurling维数,其定义如下.可数集Λ⊂d的α阶上、下Burling密度定义为
这里,B(x,r)为球心在x,半径为r的闭球,#E表示集E的势.称数
为集Λ的上Beurling维数,记为dimBΛ.
当d=1,μ为[0,1]上的Lebesgue测度时(此测度为谱测度),可数集Λ是否为L2(μ)的框架谱可用1阶上下Beurling密度来刻画[11-13].对于分形测度,Jorgensen和Pedersen[14]证明了四分Cantor测度是谱测度;对于由自仿迭代函数系所确定的自仿测度μ,文献[4]证明了在一定条件下,框架谱的Beurling维数等于此测度支撑集的Hausdorff维数.那么此结论能否推广到谱或谱测度呢?很不幸的是,对于四分Cantor谱测度而言,这个答案是否定的:它存在上Beurling维数为0的谱.一个有趣的开问题是:此谱测度谱的上Beurling维数和Beurling密度是否具有连续性.本文利用构造法,对一类框架谱测度(或谱测度),证明了其框架谱(或谱)的上Beurling维数和上Beurling密度具有连续性.如下为主要结果,其中d中的距离和测度δ0在下节给出.
定理1设μ为d中一个框架谱测度(或谱测度),Λ为其一个框架谱(或谱).如果0≤α≤dimBΛ,且s满足:若α=0,则s=∞;若0<α 直线上原点的Dirac测度记为δ0.从此节开始,均假定μ为d上非原子的Borel测度,且记ρ=μ×δ0.设a=(a1,…,ad),b=(b1,…,bd)∈d,定义 d(a,b)=max{|ai-bi|:1≤i≤d}. 闭球B(x,r)={y∈d:d(x,y)≤r}.定义μ的Fourier变换为 引理1[15]可数集Λ为μ的谱当且仅当对任意ξ∈d有 引理21)若μ是框架谱测度,Λ={λn}为其一个框架谱,则ρ为框架谱测度,且对任意{an}⊂R,集Λρ={(λn,an)}均为ρ的框架谱. 2)若ρ是框架谱测度,且有谱Λρ={(λn,an)},则μ为框架谱测度,且Λ={λn}为其一个框架谱. 3)若将框架谱测度和框架谱分别替换为谱测度和谱,上述结论仍成立. 证明设h(x,y)∈L2(ρ),那么y=0.从而f(x)=h(x,0)∈L2(μ).注意到 这表明 设λ∈n,a∈,则 〈f(x),e2πi〈x,λ〉〉L2(μ). 1)设A为μ的下框架界.那么对任意{an}⊂R,有 即下框架界条件成立.类似可证上框架界条件成立.从而ρ为框架谱测度,且Λρ为相应的框架谱. 2)设A为测度ρ的下框架界,那么 即下框架界条件成立.类似可证上框架界条件成立.从而μ为框架谱测度,且Λ为相应的一个框架谱. 3)注意到对任意a,η∈, 条件μ为谱测度,Λ为其一个谱,等价于下面恒等式成立: 它等价于ρ为谱测度,Λρ为其一个谱. 引理3设Λ={λ1,λ2,…}⊂d,Λ′={(λn,an):n≥1},其中诸an为实数,则对任意α≥0,有 证明当z=(x,y)∈d+1和r>0时,若(λn,an)∈B(z,r),则an∈B(y,r).因此 #Λ′∩B(z,r)≤#{an}∩B(y,r). 则由上Beurling密度的定义可以导出所需结论. 下面均假定实数列{rn}满足 引理4设α>0和s∈[0,+∞],令 (1) 其中k为满足rk≤r 证明对于n≥1,1≤j≤bn和m=0,1,定义 (2) (1)式左边不等式成立.下证右边不等式. 所以,当y∈时,至多存在一个不小于k的整数(记其为n),使得Γ(n)与B(y,r)相交非空.因此集Γ(n)∩B(y,r)的势不超过 当s=0时,取K=(r/log logr)α;当s∈+,取K=s·rα;当s=+∞时,取K=rαlog2r.直接验算,知若2j>K,则因此,倘若f(r)为题设所给,则有 #Γ(n)∩B(y,r)≤f(r)rα. 综上,对任意y∈,由{rn}的快速增长性,有 本节将给出主要定理的证明,为此先给出3个引理. 证明令a2n-m=(-1)m2n,n≥1,m=0,1.记Γ={an:n≥1},Λρ={(λn,an):n≥1}.注意到差分序列{a2(n+1)-m-a2n-m=2n}为严格单增序列,所以对于任意r>2, 于是当r充分大时,若n≥2log2r,则 |a2n-1|=|a2n|≥22log2r=r2>2r. 所以#Λρ∩B(0,r)<2log2r.设α>0,那么 故由引理3知dimBΛρ≤α.故dimBΛρ=0. 对于后一结论,设Λρ={(λn,an):n≥1}为ρ的一个(框架)谱,那么由引理2 2)知Λ={λn:n≥1}为μ的一个(框架)谱.注意到μ的(框架)谱是无穷集,故#Λρ=+∞.因此 所以后一结论也成立. 引理6设μ,ρ,Λ如引理5所给,且dimBΛ>0,则对于任意0<α 证明因为dimBΛ>0,所以当α∈(0,dimB(Λ))时有 (3) 因此存在实数列{rn}和d的点列{xn}使得 挑选{rn}的子列(不妨依旧记为{rn}),使之满足引理4的要求并且满足下述不等式, 其中cn为引理4所给.令an,j,bn,f(r)和Γ(n),Γ1亦为引理4所给.那么, 任取Λ∩(B(xn,rn)B(xn-1,rn-1))中含有2bn个元的子集,并记其为Λ(n)={λin,1,…,λin,2bn}.设I=N(∪n,j{in,j}),并令Γ2={ak:k∈I}为中任一上Beurling维数为0的点列. 由引理4知, 因此Λρ(n)⊂B(zn,rn).所以 从而 综上,当s为正实数时,引理结论成立.当s=0时,上述下界证明表明当β<α时, 而当s=+∞时,上述上界证明表明当α<β 所以dimBΛρ=α.因此Λρ即为所求. 当n充分大时,有 故Λ∩(B(xn,rn)B(xn-1,rn-1))的势不小于 (4) 因此当0 所以dimB(Λρ)=α.证明完毕. 定理1的证明定理的结论分为三种情形:α=0;α∈(0,dimBΛ)和α=dimBΛ.而这三种情形分别被引理5、6、7所证,所以定理结论成立.1 预备知识

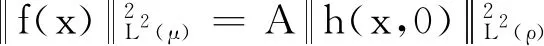
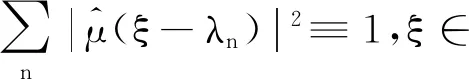
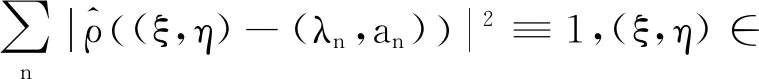

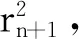
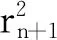
2 主要结论及其证明