一类差分不等式解的估计

陈立强，王五生

(河池学院数理学院，广西 宜州 546300)

1919年，格隆沃尔—贝尔曼(Gronwall-Bellman)[1-2]在研究微分方程的解对参数的连续性依赖时，有了下面的不等式：

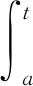
(1)

其中，常数c≥0，对未知函数u(t)有下面的估计,

在微积分不等式理论研究中，格隆沃尔—贝尔曼型积分不等式是研究Differential Equation (DE)、Integral Equation(IE)和 Differential-Integral Equation (I-EE)的解等一系列理论的重要工具，这些类型方程解的存在与否、如果存在是否唯一、进而这些解是否有界、显式解是否能容易的表出等定性性质是可以看成格隆沃尔—贝尔曼型积分不等式的推导结果.继而，格隆沃尔—贝尔曼型积分的各种推广形式开始为学者们所研究，其应用也越来越广，本文可做为其成果之一.然而，查看当前文献发现，积分号内不含未知函数导函数的积分不等式已有研究，例如文献[3-7]及其引文.此外，Pachpatte[8]研究了下面的不等式：

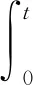
t∈+.

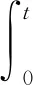
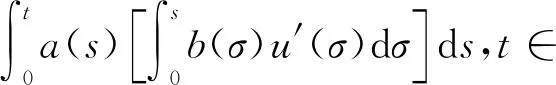
随着不等式理论研究的推进，数学家开始关注格隆沃尔—贝尔曼型不等式的离散形式及其推广形式，见文献[9-12].这方面，Pachpatte[13]研究了以下差分不等式：

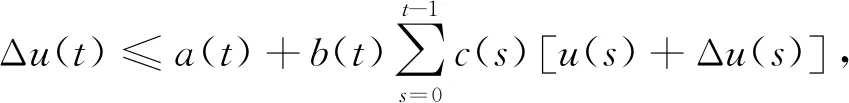
t∈0，

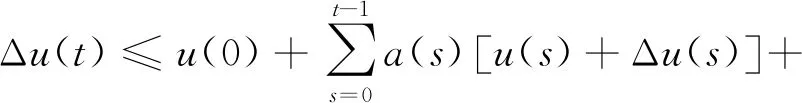
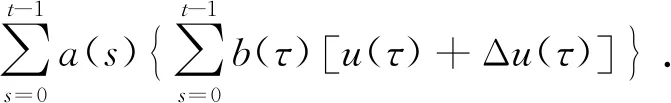
Akin-Bohner等[14]研究了下面的不等式，这个积分不等式与其他不等式重要不同在于其带有时标和线性，

t∈T0，

Zareen[15]研究了下面的不等式：

t∈+.

Kendre和Latpate[16]研究了Volterra-Fredholm型积分不等式：

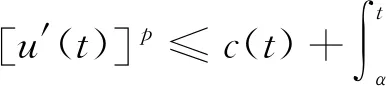
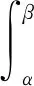
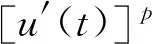
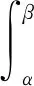
文献[17]研究了下面的积分不等式：

(2)

作者把一维的积分不等式拓展到二维的积分不等式.

在文献[18]中Cheung利用Ou-Yangh和Pachpatte的思想研究了

uq(t，s)ψ(u(t，s))dsdt，

(3)

把二维积分不等式拓广到二维的p次幂的形式.

在文献[19]中Wang研究了

φi(u(t，s))dsdt.

(4)

(4)式在(2)式的基础上，把常数a扩展成二维函数，并且把(3)式中的两项和扩展成n项和.

2016年，Zhang等[20]研究了积分不等式

在形式上把Gronwall-Belllman[1-2]的常数扩展成了一般函数a(t)，而且在(4)式的基础上把p次幂放到了求和符号里并对多项积分不等式求p次幂，推动了积分不等式发展.

最近的文献[21]研究了

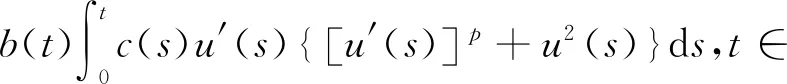
这个积分不等式研究了积分号外具有非常数因子，且积分号内含有未知函数的非线性积分不等式.

受文献[8，13-21]的启发，本文研究了一类沃尔泰拉—弗雷德霍姆(Volterra-Fredholm)差分不等式，其针对待求函数求和，且待求函数非线性.

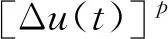
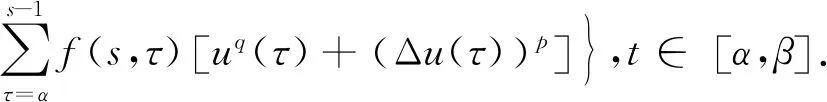
(5)

不等式(5)把文献[13]中的不等式(5)推广成非线性沃尔泰拉—弗雷德霍姆型不等式，给出了不等式(5)中未知函数的估计.最后举例说明了本结论可用来推导相应类型的沃尔泰拉-弗雷德霍姆型方程解的估计．

1 主要结果与证明

为了叙述的方便，先定义下面要用到的符号：

+=[0，∞)，α，β∈N，α<β，

ht(t，s)∶=Δ1h(t，s)=h(t+1，s)-h(t，s)．

引理1[22]令y≥0，p≥q≥0和p≠0，则对任意K>0有关系式：

引理2[16]若使得函数a(t)，b(t)，c(t)在共同的定义区间[α，β]∩上连续、非负且已知，a(t)是[α，β]∩上的单调增函数，u(t)满足：

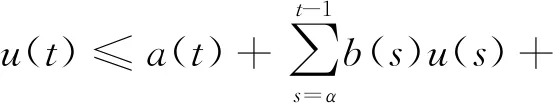
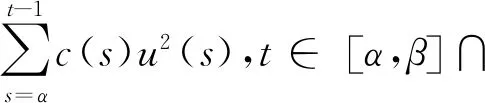
(6)

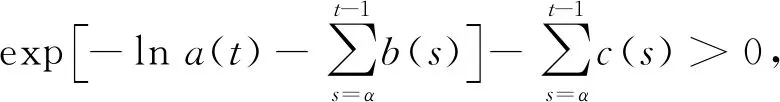
t∈[α，β]∩.

为了使下面的定理表达方便，先定义几个函数.

(7)

(8)

(2x-c(β))-1.

(9)

定理1假设不等式(5)中的函数c(t)∈C(I，+)，f(t，s)，且h(t，s)，ht(t，s)∈C(D，+)，f(t，s)，h(t，s)都是已知函数；h(t，s)当固定s关于t不减，c(t)在区间I上非减，u(α)=0，p>q>0是常数.F在+上严格递增，u(t)和Δu(t)待求，满足(5)式.∀t∈[t0，∞)，如果

则对于任意K>0，未知函数u(t)的估计式如下：

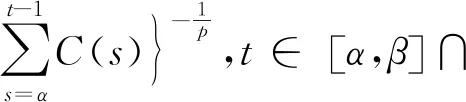
(10)

证明由不等式(5)可以推出

t∈[α，β]∩.

(11)

把不等式(11)的右端定义成函数z(t)，

t∈[α，β]∩.

(12)

那么由(12)式可看出z(t)是非减函数，且

(13)

(14)

进一步有

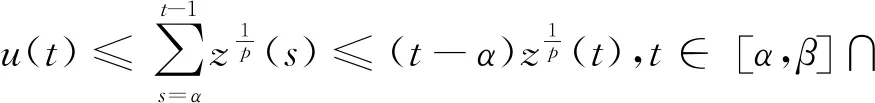
(15)

求(12)式定义的函数z(t)的差分,

(16)

把(13)式和(15)式代入(16)得到

t∈[α，β]∩.

对于任意K>0，利用引理1可以推出，

B(t)z(t)+C(t)z2(t)，t∈[α，β]∩.

(17)

其中，B(t)，C(t)满足(7)式和(8)式定义.把(16)中的t改为s，再把两边关于s从t0到t-1求和，可以得到如下结果，

t∈[α，β]∩.

(18)

显然，(18)式有(6)式的形式，其他函数具备引理2中的条件，所以，由引理2得(18)式中z的上界：

t∈[α，β]∩.

(19)

由(12)式和(14)式看出

2z(α)-c(β)=c(β)+

(20)

由(19)式和(20)式得

2z(α)-c(β)=z(β)≤

(21)

由(9)式定义，(21)式可以改写成

从而有

(22)

把(22)式代入(19)得到

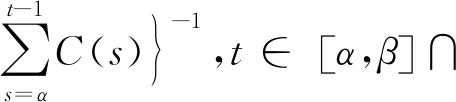
(23)

综合(15)、(23)式得(10).

2 应用

运用定理1来研究一类和差分方程解的上界，比如，有下面方程，

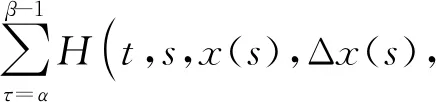
(24)

推论1假设方程(24)中G，H∈C([α，β]∩×[α，β]∩×××，)，W1，W2∈C([α，β]∩×[α，β]∩××，)满足下列条件：

|G(t，s，x，y，z)|≤h(t，s)yp(xq+yp+z)，

(25)

|H(t，s，x，y，z)|≤h(t，s)yp(xq+yp+z)，

(26)

|W1(t，s，x，y)|≤f(t，s)yp(xq+yp)，

(27)

|W2(t，s，x，y)|≤f(t，s)yp(xq+yp)，

(28)

|d(t)|=c(t)，

(29)

其中，h(t，s)，f(t，s)，c(t)以及p，q满足定理1之定义,则∀K>0，方程(24)的解x(t)的估计如下：

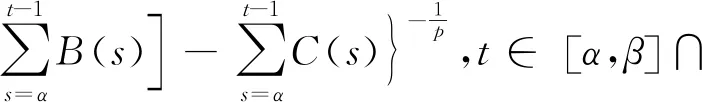
(30)

其中，B(t)，C(t)，F(t)由(7)式，(8)式和(9)式定义，且满足定理1中的相应条件．

证明根据条件(25)～(29)，由方程(24)推出

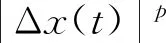
t∈[α，β]∩.

(31)

可见(31)式具有(5)式的形式，又满足定理1中的条件，由定理1可以得到所求的方程解的估计式就是(30)式．