新冠肺炎疫情演化情境下应急物资需求预测研究
李 清,苏 强
(1.上海政法学院经济管理学院,上海 200333;2.同济大学经济与管理学院,上海 200092)
2019年12月底,湖北武汉陆续发现多例肺炎患者,后被证实为是一种新型冠状病毒引起的急性呼吸道传染病.随着春节到来,人流大规模大范围移动,该病毒逐渐蔓延,在海外很多国家和地区也相继出现,呈现出爆发式增长的趋势.截至2021年1月4日,据中国31个省、自治区、直辖市和新疆生产建设兵团的报告,累计确诊病例87 183例,累计死亡病例4 634例;累计收到中国港、澳、台地区通报确诊病例9 878例,死亡病例160例[1].全球222个国家和地区累计确诊病例85 617 337例,累计死亡病例1 852 571例.美国、印度和巴西是当时累计确诊病例人数最多的三个国家,每日新增患病感染人数以较快的速度增加,多个国家甚至出现了新冠病毒新变种,疫情传播风险进一步加大[2].中国本土疫情呈现零星散发和局部聚集性疫情交织叠加态势,防控形势仍然严峻复杂.各地仍有零星新增病例,主要以境外输入病例为主,境外输入确诊病例294例,累计确诊病例4 339例.
全球化带来的国际贸易和人口流动会扩大疫情的传播范围,使其进一步扩散和蔓延[3].为描述疫情传播趋势,国内外专家采用传染病学和数学建模等方法对新冠疫情进行了研究.中国疾控中心新型冠状病毒应急响应机制流行病学组基于截至2020年2月11日中国内地所有上报的新冠肺炎病例,分析了患者的年龄、性别、病死率、疾病传播时空特点和流行病学曲线[4].在传染病传播方面,Sun等将人群分成不同类别,建立常微分方程模型[5].张刚庆等[6]和Bolzoni等[7]分别考虑了易感者、感染者和痊愈者三类人群,建立传播扩散模型,模拟疫情传播过程.Kim等[8]和Liu等[9]采用计算机模拟和数值计算方法建立并完善传染模型.Zhao等建立指数增长模型描述2020年1月10日到24日的病例时间序列曲线,对疫情早期阶段的基本感染数量进行估计[10].随着疫情传播进程,病毒感染数量的变化,控制策略和检测技术发生了显著变化.Tang等构建动态传输模型,采用随时间变化的接触率和诊断率,对每日再生数进行重新估计,制定更好的干预措施[11].Lin等考虑个人和政府行为(延长假期、限制旅行和强化检验检疫等),建立新冠疫情概念模型,估算传染病传播中的关键因素,估计和捕捉疫情发展趋势[12].基于新冠肺炎传播机理、隔离和治疗感染者等措施的研究,白宁等建立动力学模型,预测湖北省疫情发展情况,并评估相应控制策略的有效性[13].
随着春节临近,境外回国人员增加,境内人员流动性大且聚集活动增加,进口冷链食品和货物物流增大,加大了疫情传播风险.新冠肺炎疫情在短期内并不会消失,考虑到疫情的突发特性及其带来的重大经济社会影响,国务院联防联控机制在落实个人防护措施、社会和企事业单位防控措施、行业防控责任和地方政府责任等方面提出了明确要求[14].2020年2月24日推出的《突发公共卫生事件应急管理研究之二:从抗击新冠肺炎看应急医疗资源优化配置》研究报告中强调,在公共卫生事件应急管理中,应急医疗资源是物质基础,其配置如何直接关系事件处置的及时性和有效性,优化应急医疗资源配置的意义重大[15].
针对传染病等公共突发事件的应急救援,Rachaniotis等[16]、Liu等[17]、He等[18]建立了数学规划模型,解决了救援物资的配置决策和优化问题.黄天春分析灾害生命周期各阶段中应急救援行动和网络的特性,为应急救援工作提供了技术支持[19].在传染病传播和应急救援过程中,救援物资需求量往往难以精确计算,在各方面信息不确定的情况下,Liu等以最小化生命损失为目标,探讨确保医疗救援物资的供应机制[20].基于传染病动力模型,马知恩等将人群分为易感者、潜伏者、感染者和痊愈者四类,建立SEIR模型,并根据模型对应急物资需求进行预测[21].区别于地震等突发自然灾害,传染病的传染率、治愈率和死亡率等关键信息不确定,医疗救援物资需求存在特殊性.针对难以获得精确疫情信息,葛洪磊以最小化贝叶斯风险为目标建立应急物资分配决策模型,求解最优信息观测次数和物资分配量,从时间、事件、信息特征和感染规模等7个维度将新冠肺炎疫情分成5种情境,分析每个情境下的关键因素,建立多周期贝叶斯序贯决策模型,分别提出各情境下的救援物资配置方案,并基于武汉疫情数据进行分析和验证[22-23].
目前大多数文献假设应急需求对时间因素不敏感,然而,实际救援中医疗资源需求随时间动态变化,早期医疗物资配置量会对后期需求有影响.此外,现有文献主要关注传染病传播模型和应急救援的研究,将两个方面统一集成考虑的文献不多.本文基于传染病模型构建应急物资需求预测模型,分别建立时变需求和贝叶斯序贯决策物资需求模型,为实际应急救援工作提供科学有效的预测方法.
1 时变需求物资预测模型
1.1 疫情演化阶段分析
医疗物资配置决策受新冠肺炎疫情时间、空间、感染者数量和疫情事件信息等多个因素的影响,一方面这些因素将决定采取哪种级别的防控措施,另一方面防控措施的具体执行也将影响疫情传播,缩小传染规模.疫情最早通报时间为2019年12月31号,但在12月底就发现了相关病例,其传播和发展可以总结为如表1所示的4个阶段.

表1 新冠肺炎疫情演化4个阶段Tab.1 Four evolution stages of COVID -19
根据表1中的4个阶段,考虑湖北和全国除湖北外其他省市的每日新增患病感染人数和现有患病感染人数,绘制图1和图2.
疫情初期主要出现在湖北武汉,之后传播到全国各地.产生阶段,患病感染者随着报道和排查的深入逐步被发现,新增患病感染人数逐渐增多,总人数在100以下;全国除湖北外的地区暂未发现患病感染者,但自1月20日开始出现患病感染者.爆发阶段,1月31日前湖北每日患病感染人数缓慢增长,总人数小于1 500人;之后呈现快速增长趋势,峰值的每日患病感染人数超过3 000人,总人数大于2 000人;得益于及时的交通管制策略,全国除湖北外地区的患病感染人数呈现出先缓慢增长再缓慢减少的趋势,人数在1 000人以下.高峰阶段,受疫情多次传播的影响,经全面排查湖北每日新增患病感染人数在2 000人上下波动;由于统计方式的改变,2月12日新增患病感染人数急剧增加,之后逐渐减少.这一阶段,各社区实行封闭式管理,因此,全国除湖北外地区的每日新增患病感染人数逐渐减少,疫情逐步被控制.衰退阶段,湖北每日新增患病感染人数在短暂上升后急剧下降,并从3月18日开始清零.全国除湖北外地区的每日新增患病感染人数在20人上下波动,随着复工复产的逐步实施,患病感染人数有较小幅度的上升,但是整体在可控范围内.因春节期间国内人员流动量较大,同时受到境外人员和货物输入的影响,在衰退阶段国内一些省市仍存在零星病例.
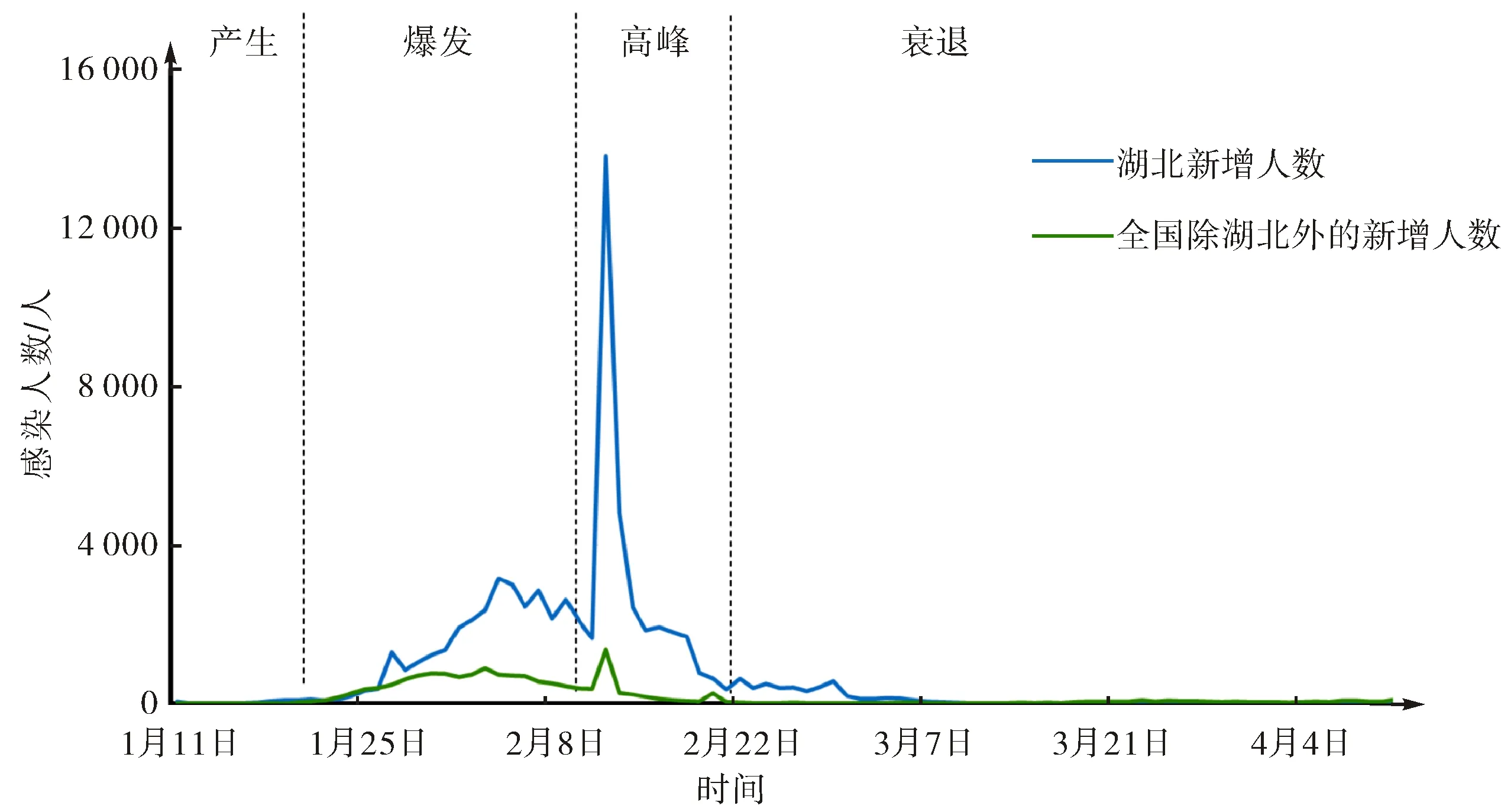
图1 新冠肺炎不同阶段每日新增患病感染人数Fig.1 Number of new infections per day at different stages of COVID -19
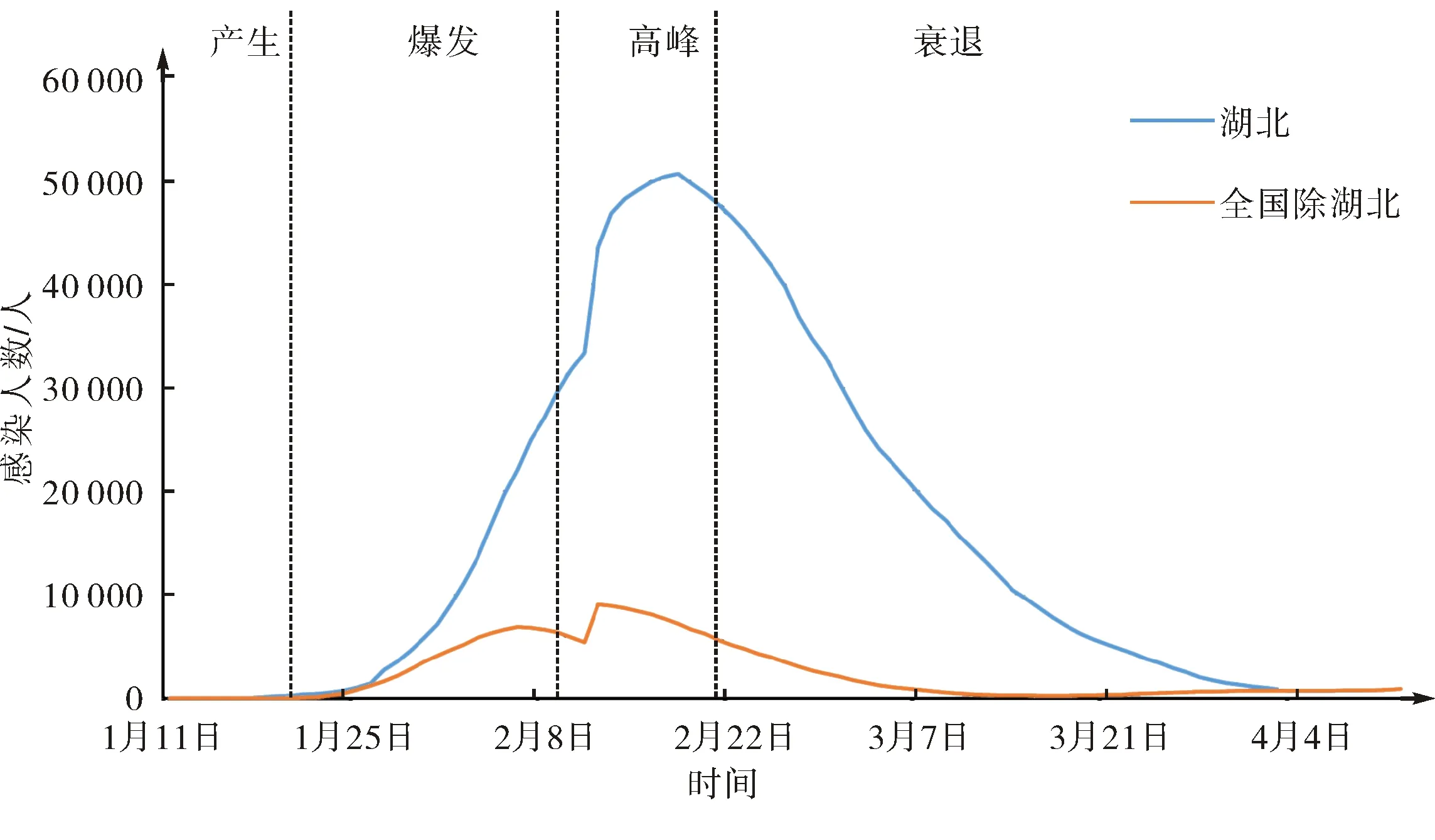
图2 新冠肺炎不同阶段患病感染人数Fig.2 Number of infections at different stages of COVID-19
1.2 疫情SEIR模型
基于新冠疫情演化特征,考虑隔离措施的影响,本文建立SEIR模型模拟疫情传播和发展趋势.在疫情产生、传播、爆发和衰退整个过程中,感染者、康复者和死亡者数量随时间不断变化,而医疗物资需求量与感染者数量息息相关,因此首先预测患病感染者和潜伏期感染者数量,接着计算医疗救援物资和防护物资的需求量.
基于SEIR模型[9],不考虑人口迁徙、自然出生和死亡,本文将人群N分为易感、潜伏、感染、痊愈和死亡五类.其中,S(t)表示t时刻易感者数量,也即t时刻健康人群数量;E(t)为t时刻潜伏期感染者数量;I(t)为t时刻患病感染者数量;R(t)为t时刻痊愈者数量;D(t)为t时刻死亡者数量.五类人群间的转换关系如图3所示.
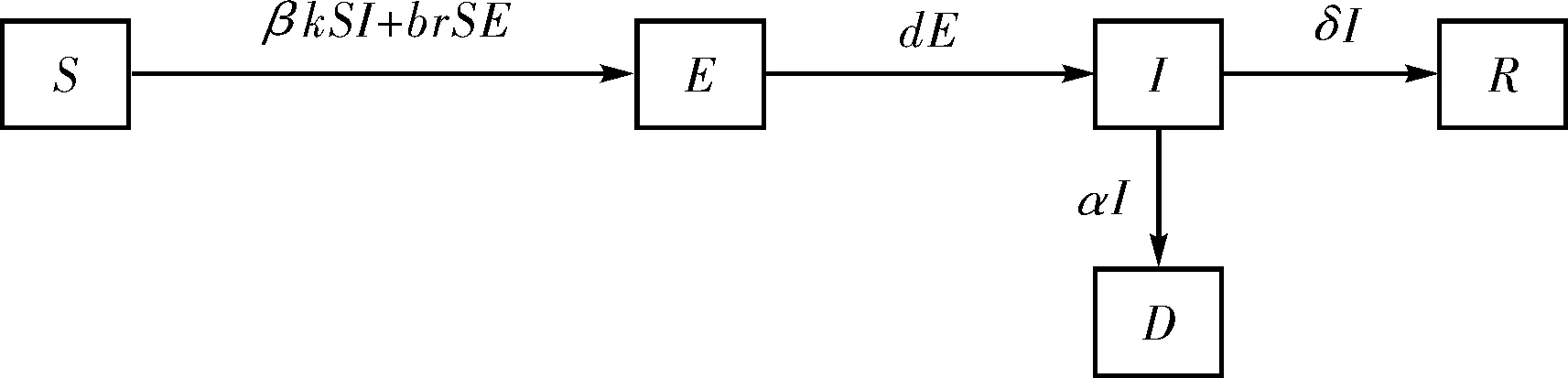
图3 SEIR模型Fig.3 SEIR model
基于图3构建如式(1)~(6)的微分方程模型:
N=S(t)+E(t)+I(t)+R(t)+D(t),
(1)
S(t+1)=S(t)-βkS(t)I(t)-brS(t)E(t),
(2)
E(t+1)=E(t)+βkS(t)I(t)+
brS(t)E(t)-dE(t),
(3)
I(t+1)=I(t)+dE(t)-(α+δ)I(t),
(4)
R(t+1)=R(t)+δI(t),
(5)
D(t+1)=D(t)+αI(t),
(6)
其中,β表示患病感染者的传染概率;k表示每个患病感染者平均接触的人数;b为潜伏期感染者的传染概率;r为每个潜伏期感染者平均接触的人数;d表示潜伏期感染者患病概率;α为死亡率;δ为康复率,β,b,d,α,δ>0.在实际观测中发现潜伏期感染者经过潜伏期后有一定的概率转为健康患者,因此,引入n表示潜伏期感染者转为健康人群的概率,τ表示潜伏期,则当t>τ时,易感者和潜伏期感染者的转换方程如式(7)和(8)所示.
S(t+1)=S(t)-βkS(t)I(t)-
brS(t)E(t)+nE(t),
(7)
E(t+1)=E(t)+βkS(t)I(t)+
brS(t)E(t)-dE(t)-nE(t).
(8)
在疫情实际传播中,国家和地方均出台了相关的管控措施.2020年1月23日,武汉实行交通管制,2月11日开始,全国的社区实行封闭式管理.在上述SEIR模型中,考虑管控措施对疫情传播的影响,实行管制后,对患病感染者和潜伏期感染者平均接触人数进行调整,即降低k和r这两个参数的值.
1.3 医疗物资需求预测模型
基于SEIR模型,本文建立医疗物资需求预测模型[17].假设t时刻医疗物资需求量是关于患病感染人数的函数,如式(9),通常采用线性函数形式,即式(10),其中a为系数.
dt=f[I(t)],
(9)
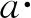
(10)
对于口罩和防护服等每天或每隔一段时间需要更换的物资,其需求为患病感染者的函数,根据式(9),可以得到t和t+1时刻该类物资需求量分别为dt和dt+1.对于呼吸机和床位这类可以反复使用的物资,其需求量会随时间变化,早期医疗物资配置会在一定程度上减缓疫情,并影响后期物资实际需求量.实际应急救援中,t时刻可能会有pt单位的救援物资到达.在这种情况下,t+1时刻实际需要配送的物资量为dt+1-pt,而不是dt+1.引入因子ηt,建立式(11)衡量前期物资配置量对后期物资需求的影响.
(11)
患病感染者接受一定时间的治疗后恢复健康,假设患病感染者的治疗周期为Γ,有效治愈率为δ,得到t=1时刻的医疗物资需求量,如式(12)所示;t=2和t=3时刻的医疗物资需求量,分别如式(13)和(14)所示.
(12)
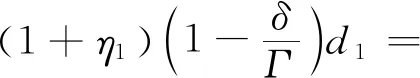
(13)
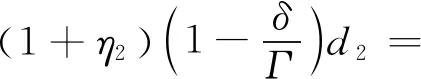
(14)
由式(12)~(14),得到递推公式(15),也即t=n时刻的医疗物资需求量.
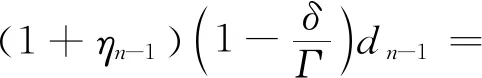
(15)
以每天为一个决策周期,计算得到时变需求下每天的物资需求量.
2 基于贝叶斯序贯决策的物资预测模型
在疫情演化过程中,信息不确定且实时更新,应用贝叶斯决策可以建立更符合实际的物资预测模型.采用贝叶斯分析对收集到的信息进行更新,建立贝叶斯序贯决策模型,以1 d作为决策周期对疫情信息进行观测;基于先验信息和观测得到的信息,采用贝叶斯方法计算后验信息;根据每个周期的后验信息预测物资需求量.为充分利用初始先验信息和每个周期的观测信息,将每个周期的后验信息作为后一周期的先验信息,根据观测信息不断推进,降低信息不确定性[23].
2.1 符号定义
t:决策周期,t∈T;
β:患病感染者的传染概率;
It:t周期(时刻)患病感染者数量;
ω:每个患病感染者在每个决策周期需要的单位物资数量;
nt:t周期传染概率观测次数;
Vt:t周期物资需求量.
2.2 模型构建
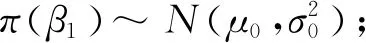
当物资预测量小于需求量时,决策产生损失.在观测到信息后再制定物资需求决策,无法满足观测信息前的需求,造成物资配置延迟,产生延迟损失.由于疫情信息不确定导致物资配置不能满足实际需求,造成失误损失.第t周期的延误损失、失误损失和加权损失函数分别如式(16)~(18)所示:
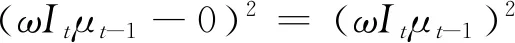
(16)
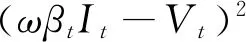
(17)
(18)
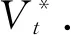
(19)
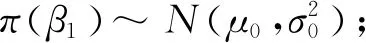
(20)
3 算例分析
3.1 预测患病感染人数与实际患病感染人数对比
采用SEIR模型对湖北每日新增患病感染人数进行预测,参考相关文献和报道[13],模型中相关参数的定义和取值见表2.
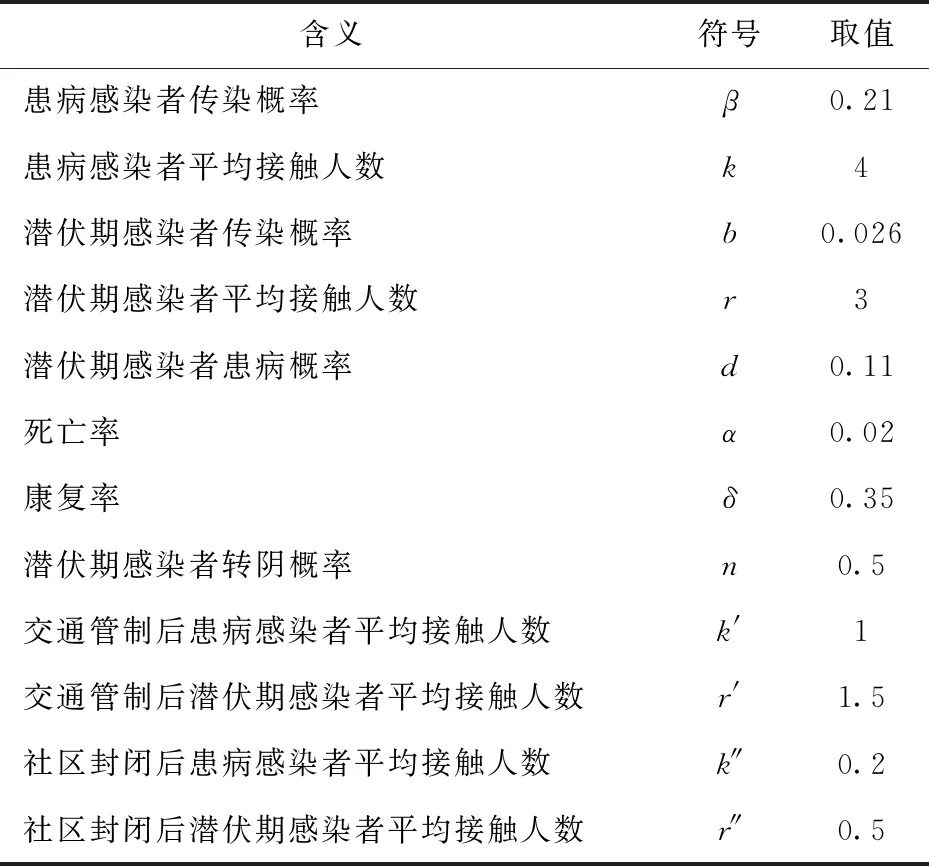
表2 参数定义和取值Tab.2 Parameter definitions and values
湖北省总人口计为59 170 000.从2020年1月11日开始统计,11日湖北有患病感染人数41人,SEIR模型预测的每日患病感染人数与实际每日患病感染人数如图4.
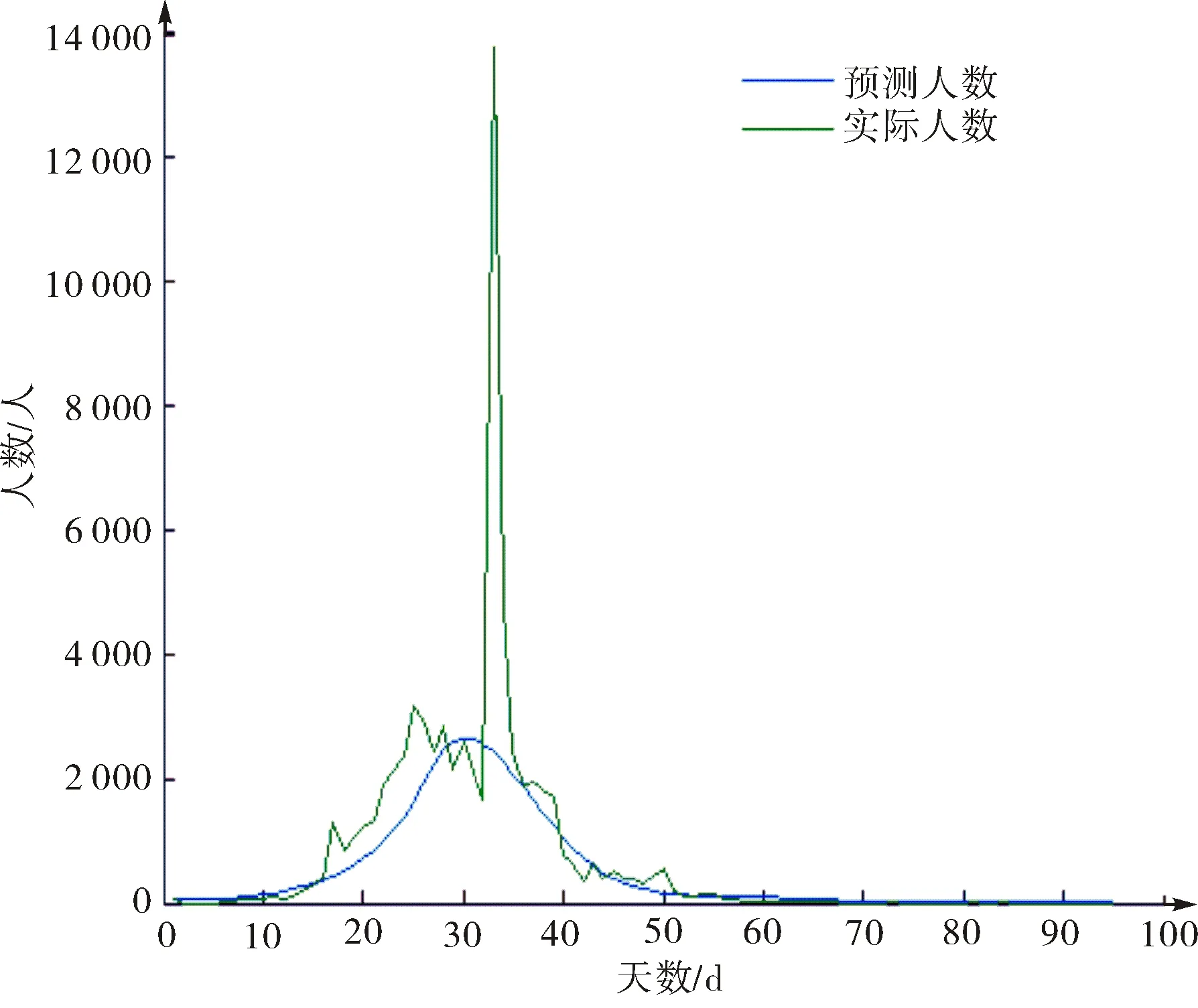
图4 预测患病感染人数与实际人数比较Fig.4 The predicted number of infections compared with the actual number
图4中蓝线为预测每日患病感染人数,绿线表示实际每日患病感染人数.两条曲线的走势大致相同,相关系数为72.58%.
受到统计标准影响,2月12日(第33天)出现了非常大的峰值,模型出现较大误差.因此,以2月11日(第32天)和13日(第34天)新增患病感染人数的平均值代替原始数据,对其进行修正.此外,1月11日湖北新增患病感染人数为41例,受到初期检测技术和排查范围的影响,接下来的4 d新增患者数量均为0.为进一步降低误差,以1月16日(第6天)作为初始时刻统计患病感染人数.
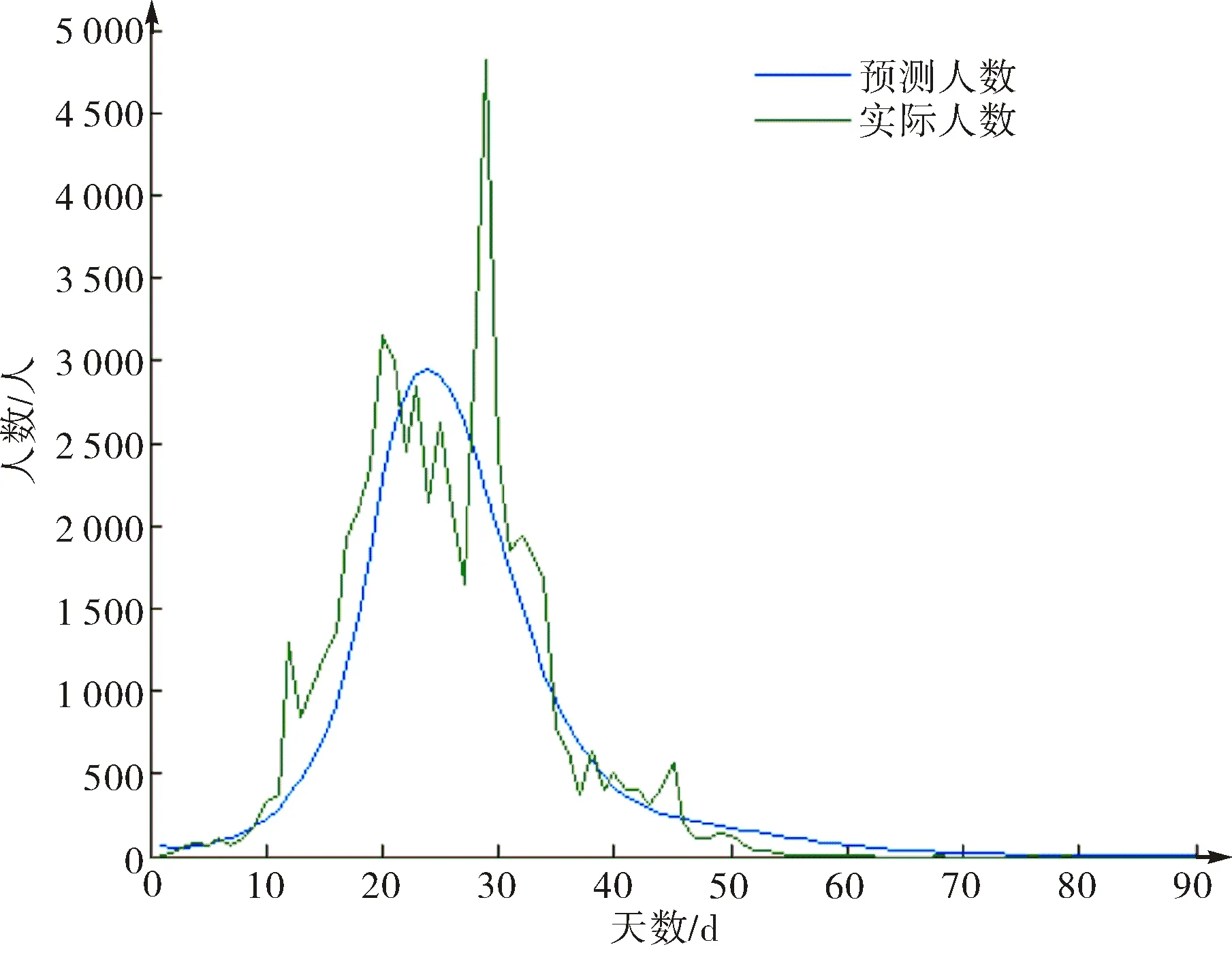
图5 预测患病感染人数与实际人数比较(修正)Fig.5 The predicted number of infections compared with the actual number (revision)
采用1月16日到4月14日这90 d的数据对预测模型进行修正,结果如图5所示.预测每日患病感染人数与实际每日患病感染人数的相关系数达到91.83%,SEIR模型与实际情况贴合较好,模型能较准确地描述疫情演化情况.
3.2 基于时变需求模型的物资需求预测
采用时变需求模型计算每日物资需求量,假设患病感染者治疗周期为Γ=15,有效治愈率为δ=0.25,a=1表示每个患病感染者每日物资需求量为1个单位.
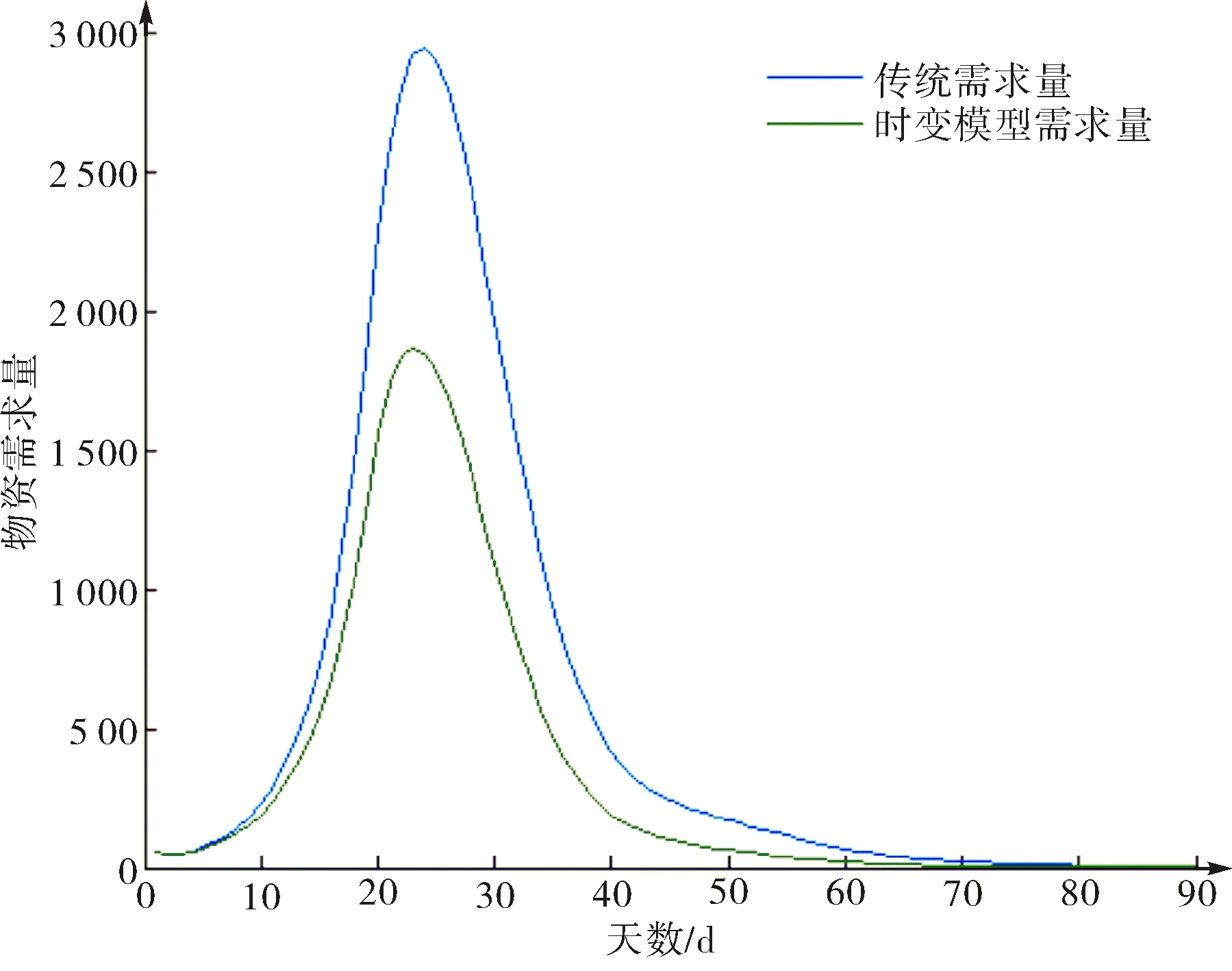
图6 基于预测患病感染人数的时变需求模型物资需求量Fig.6 The material demand of time varying model based on the predicted number of infections
采用SEIR模型预测每日患病感染人数,根据式(10)计算传统物资需求量,如图6蓝线所示.根据式(15)计算时变物资需求量,如图6绿线所示.两条曲线趋势一致,时变需求量在期初与传统需求量一致,之后逐渐小于传统需求量.
根据实际每日新增患病感染人数,分别计算传统物资需求量和时变物资需求量,具体如图7.
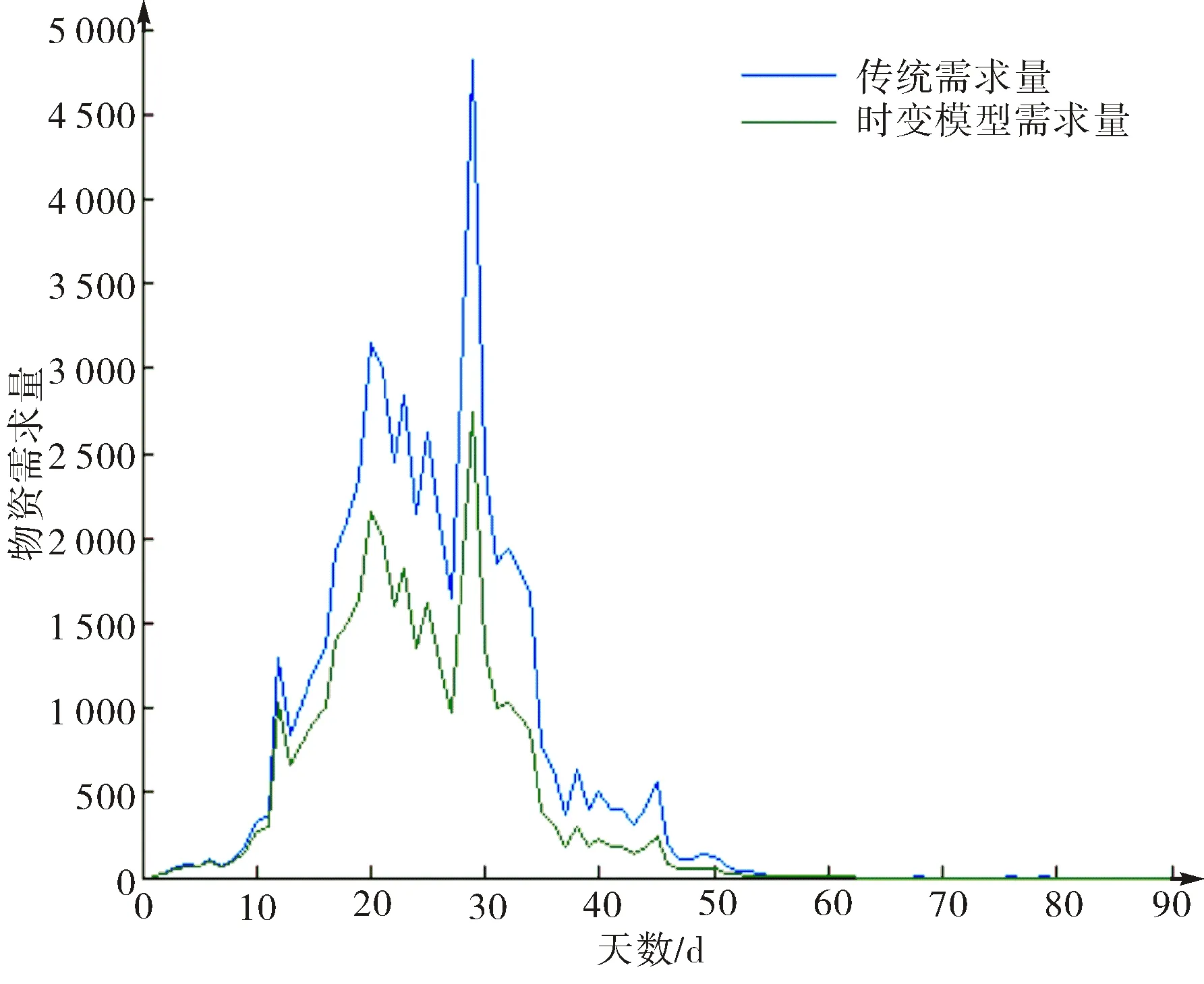
图7 基于实际患病感染人数的时变需求模型物资需求量Fig.7 The material demand of time varying model based on the actual number of infections
根据式(10)计算传统物资需求量,如图7蓝线所示.根据式(15)计算时变物资需求量,如图7绿线所示.考虑到前期物资配给量对后期需求量的影响,时变需求量整体小于传统需求,时变需求曲线与传统需求曲线的趋势基本一致.
3.3 基于贝叶斯序贯决策的物资需求预测
假设决策周期初始湖北省的感染率服从均值为1.019 8,标准差为0.543 4的正态分布[23],每日观测次数为随机生成的正态分布随机数,取值范围为1到4.当一天有多次观测时,取多个观测值的平均值和标准差作为观测均值和标准差.根据每一天患病感染人数计算当天感染率,并与期初的感染率相比较,求得下一周期感染率的均值和标准差.采用贝叶斯序贯决策模型预测物资需求量,并与传统需求进行比较,具体如图8、图9所示.
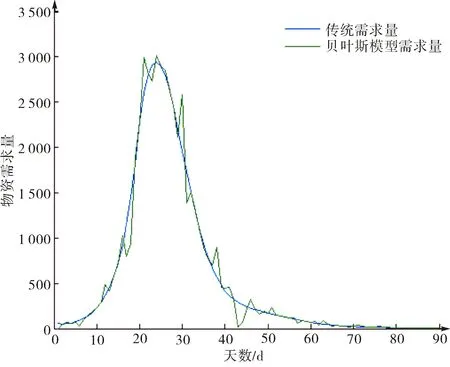
图8 基于预测患病感染人数的贝叶斯序贯决策模型物资需求量Fig.8 The material demand of Bayesian sequential model based on the predicted number of infections
基于SEIR模型对每日患病感染人数进行预测,根据式(10)计算得到传统物资需求量,如图8中蓝线所示.根据式(20)计算贝叶斯模型物资需求量,如图8中绿线所示.贝叶斯模型需求量受传染概率影响,呈现出上下局部波动的趋势.
根据实际每日新增患病感染人数,计算传统物资需求量和贝叶斯模型物资需求量,分别如图9中蓝线和绿线所示.假设传染概率不断更新,根据前一阶段的先验概率和这一阶段的观察值求得这一阶段的传染概率,不断调整传染概率值.贝叶斯模型需求量与传统物资需求量的趋势一致,两条曲线贴合情况较好.
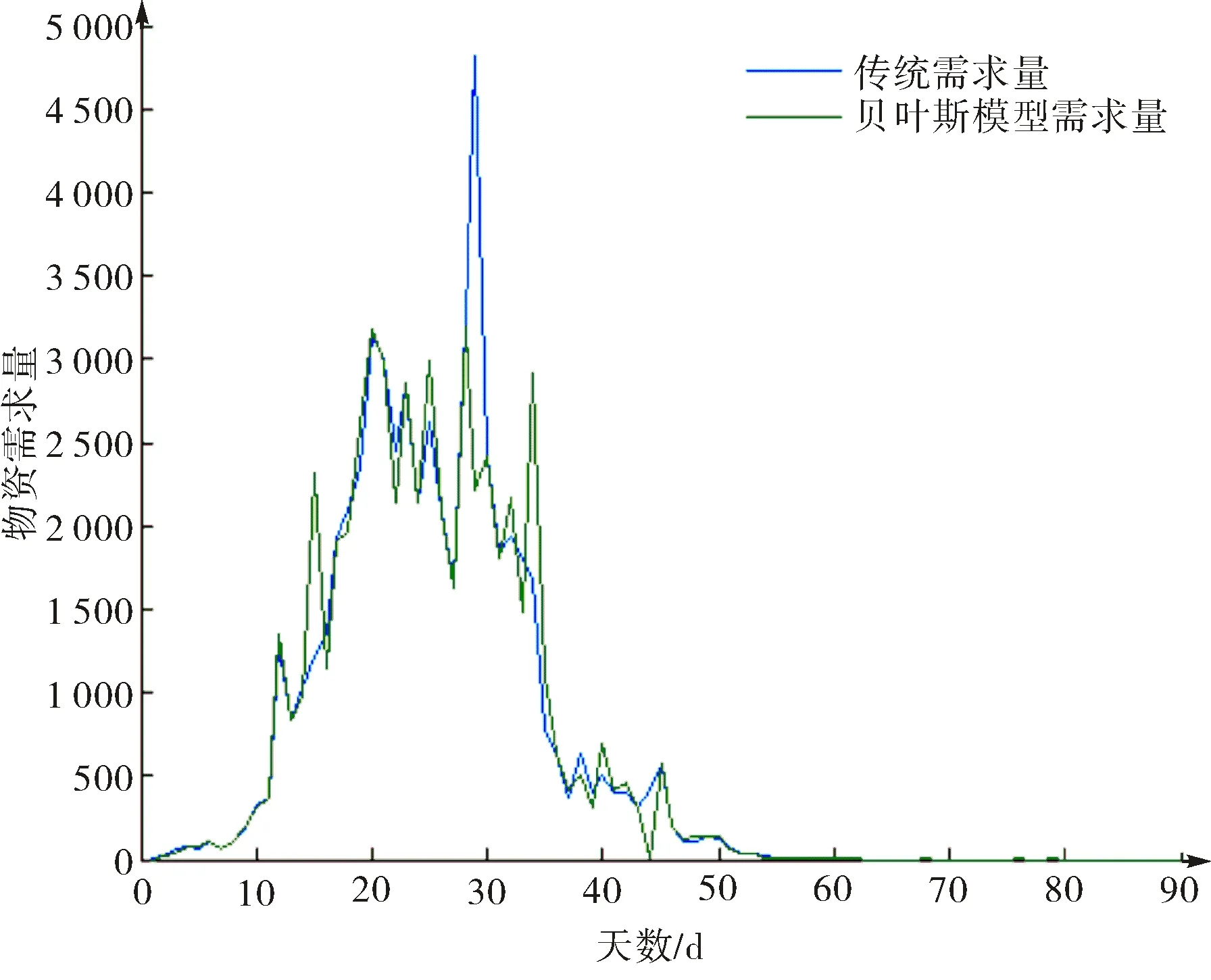
图9 基于实际患病感染人数的贝叶斯物资需求量Fig.9 The material demand of Bayesian sequential model based on the actual number of infections
3.4 两种需求预测模型的比较
根据预测患病感染人数,分别采用时变需求模型和贝叶斯模型对物资需求进行预测,两种模型与传统物资需求量的误差见图10.
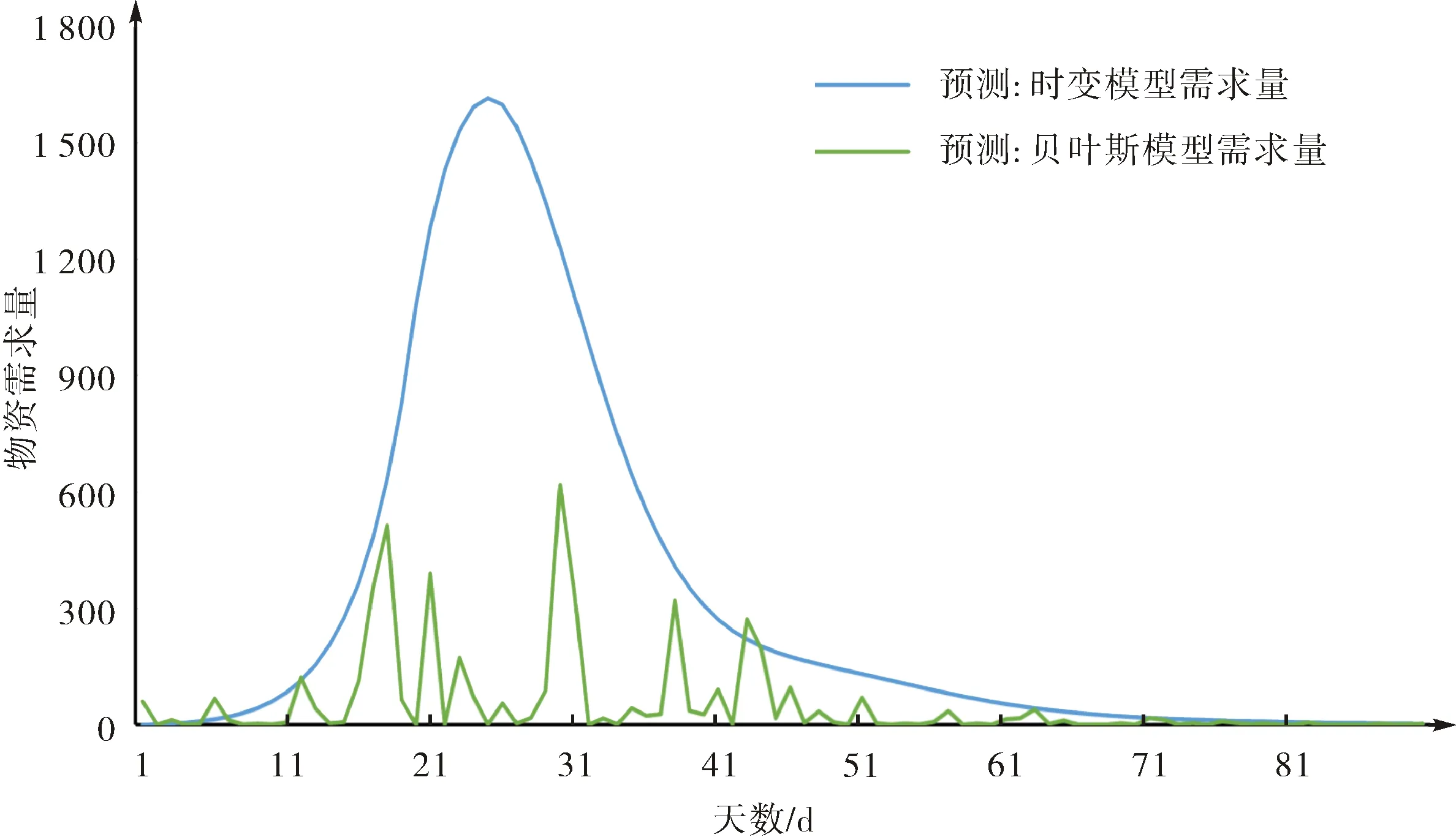
图10 基于预测患病感染人数的两种模型的需求预测误差Fig.10 Demand forecasting errors of the two models based on the predicted number of infections
时变需求模型的误差逐步增加,到达峰值后逐步减小,最后趋于0;患病感染人数越多,误差越大.贝叶斯模型的物资预测量受到传染概率影响,误差呈现出随机波动趋势,并随着患病感染人数减少逐渐变小.
根据实际患病感染人数,分别采用时变需求模型和贝叶斯模型对物资需求进行预测,两种模型与传统物资需求量的误差见图11.
时变需求模型的误差与实际患病感染人数趋势一致,先逐渐增加,到达峰值后逐步减小,最后趋于0.患病感染人数越多,误差越大.贝叶斯模型的物资预测量受到传染概率的影响,其误差呈现出随机波动的趋势,出现峰值的日期与患病感染人数出现峰值的日期基本一致.
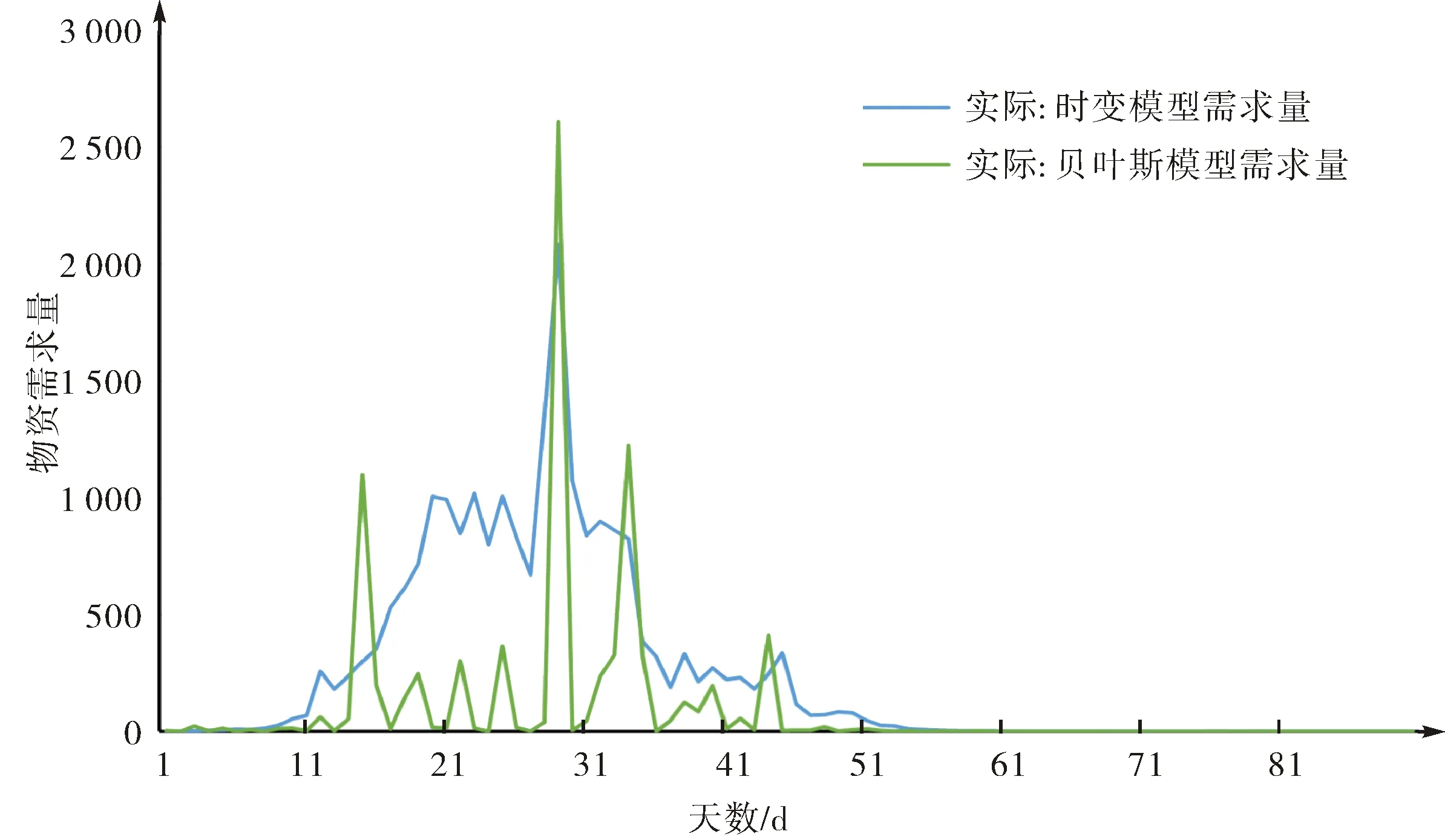
图11 基于实际患病感染人数的两种模型的需求预测误差Fig.11 Demand forecasting errors of the two models based on the actual number of infections
基于预测和实际患病感染人数两种情况,时变需求模型和贝叶斯需求模型与传统需求的总误差统计见表3.
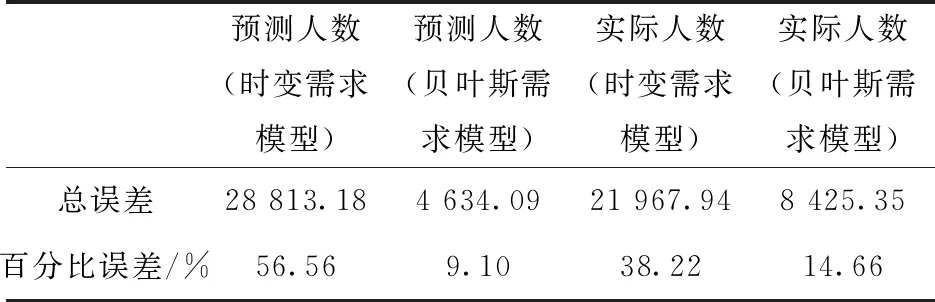
表3 两种模型总误差Tab.3 Total errors of the two models
基于预测患病感染人数,时变需求模型和贝叶斯需求模型与传统需求量的总误差分别为28 813.18和4 634.09.规划周期内预测患病感染人数的总和为50 943人,因此,其百分比误差分别为56.56%和9.10%.基于实际患病感染人数,时变需求模型和贝叶斯需求模型与传统需求量的总误差分别为21 967.94和8 425.35,规划周期内实际患病感染人数的总和为57 477人,因此,其百分比误差分别为38.22%和14.66%.两种情况下,贝叶斯需求模型的误差均小于时变需求模型.
4 总结
新冠肺炎疫情自2019年12月底出现后在全世界传播蔓延,引起了全球的广泛关注.目前,我国总体上疫情防控局势稳定,但各地仍不时出现零星病例,而国外疫情态势仍十分严峻.本文根据代表性事件和患病感染人数特征,将新冠肺炎疫情的传播演化分为产生—爆发—高峰—衰退四个阶段,分析每个阶段的特征.基于经典SEIR模型,考虑本次疫情的隔离措施和潜伏期感染者转阴特征建立传播模型,预测每日患病感染人数.根据预测患病感染人数和实际患病感染人数,采用时变需求模型预测每日物资需求量.最后,考虑传染概率不断更新的情况,建立贝叶斯序贯决策模型预测每日物资需求量.在预测和实际患病感染人数两种场景下,贝叶斯模型的与传统需求模型的误差均小于时变需求模型的.
面对突如其来的疫情和不断变化的形势,政府加强信息平台建设,实时更新疫情信息,可有效防止小道消息和谣言散播而加剧群众恐慌,引起物资哄抢或其他恶劣行为.与此同时要制定并完善应对大规模传染病的应急预案,建立针对不同灾难的应急物资储备体系,同时有效开展物资生产和运输活动,保证疫情重点区域和其他区域的物资稳定快速供应,为疫情防控提供重要物质基础.另外,还需要建立科学的物资预测和配送体系,根据实时更新的信息预测物资需求并制定合理的物资分配方案,要防止仓库物资堆积如山居民却物资供应不足的情况出现,确保物资能得到有效利用.
此次新冠肺炎疫情在老年患者中传染概率较高,且男性患者比例高于女性.此外,除了传染概率,康复率、死亡率和潜伏者转阴概率也随着时间不断变化.进一步的研究中,可以在SEIR模型中考虑年龄和性别等因素,建立更符合新冠疫情的传播模型;同时考虑其他关键信息的不断更新,以更准确预测物资需求量.

