含p-Laplacian无穷点边值问题正解的存在性

王 和 香

(喀什大学数学与统计学院，新疆 喀什 844006)

近年来，随着人们对非连续介质电动力学、聚合物流变学、黏弹力学、分形和混沌等问题的深入研究，发现在解决问题过程中，利用分数阶构建的模型比整数阶模型更适用、提供的方法也更多样化.因此，对于分数阶微分方程的研究越来越受到学者们的重视，这也极大地促进了含p-Laplacian算子的分数阶微分方程边值问题的发展．

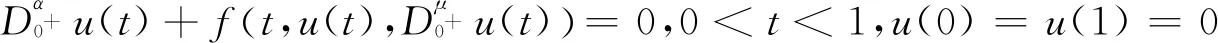
多重正解的存在性.受以上文献启发，本文将研究一类具p-Laplacian算子的无穷多点边值问题：

(1)

正解的存在唯一性，其中0<γ≤1，α≥2，n-1<α≤n，0<β<α-1，ηi∈，是标准的Riemann-Liouville导数，φp为p-Laplacian算子，满足且

f是在[0，1]×[0，+∞)→[0，+∞)上的连续函数，a(t)∈C((0，1)，[0，+∞))，当t=0，1时奇异．

1 预备知识与引理

定义1[4]函数y:(0，+∞)→R的α>0阶Riemann-Liouville积分是指

其中[α]表示α的整数部分，右边是在(0，+∞)上逐点定义的．

定义2[4]函数y:(0，+∞)→R的α>0阶Riemann-Liouville微分是指

n=[α]+1，

其中[α]表示α的整数部分，右边是在(0，+∞)上逐点定义的．

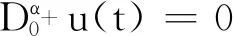
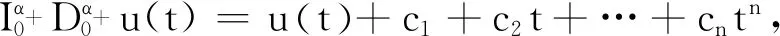
定理1[5](Arzela-Ascoli定理)设{f(t)}是定义在α≤t≤β上的一致有界且等度连续的实函数族，则从其中必可选取一个在α≤t≤β上一致收敛的函数列{fn(t)}．

为简化计算，假设如下条件成立：

(A1)p(0)≠1，q(s)≥0，s∈[0，1]；

给出如下记号，设

K(t，s)=

G(t，s)=K(t，s)+q(s)tα-1，

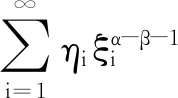
注记2若ηi=0，(i=1，2，…)，则p(s)≡0，q(s)≡0;若ηi≥0(i=1，2，…)，且p(0)<1，则q(s)≥0，s∈[0，1]．

引理3[6]设y∈L[0，1]且p(0)≠1，则边值问题

(2)

引理4[6]函数K(t，s)具有以下性质:

1)K(t，s)>0，∀t，s∈(0，1);

其中,h(s)=[1-(1-s)β](1-s)α-β-1，M1=max{1，β-1}．

引理5[6]引理3中定义的Green函数具有如下性质：

1)G(t，s)>0，∀t，s∈(0，1);

2)G(t，s)≤tα-1Φ1(s)，∀t，s∈[0，1];

3)tα-1Φ2(s)≤G(t，s)≤M1Φ2(s)，∀t，s∈[0，1]，

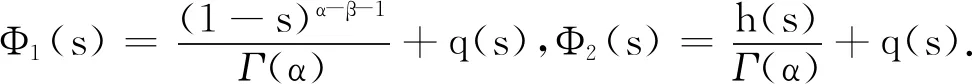
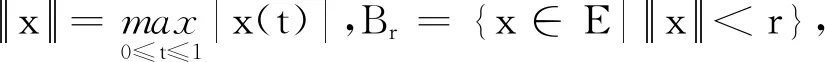
P={x∈E:x(t)≥0}，

引理6边值问题

(3)

有唯一解

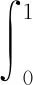
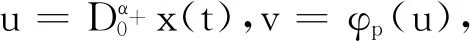
(4)

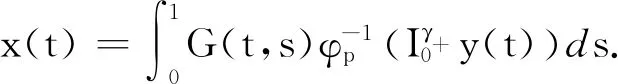
引理7假设条件(A1)和(A2)成立，则BVP(1)有唯一解

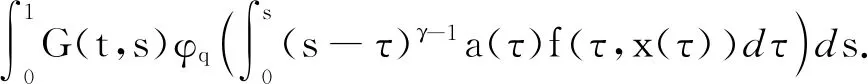
证明过程同引理6．

引理8定义算子A:P→E，

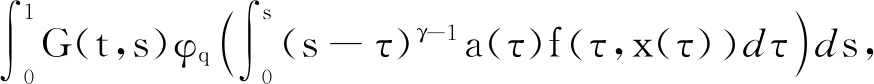
则A:P→Q全连续．

证明A:P→Q.由引理5，易证A:P→Q，再由Arzela-Ascoli定理，可证A:P→Q全连续．

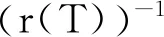
2 主要结论

给出以下条件：

(H1)f(t，0)在[0，1]上不恒为0；

x，y∈[0，+∞)；

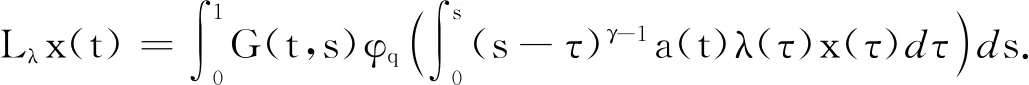
定理1若条件(H1)-(H4)成立，则BVP(1)有唯一正解．

证明因为f(t，0)≠0，所以0不是A的不动点.故只需证明A在Q中存在唯一解．

首先，证明解的存在性．

设Q1={x∈P:∃l1，l2，使得l2tα-1≤x(t)≤l1tα-1}，对∀x∈Q{0}，设

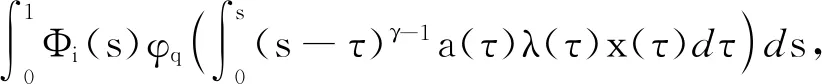
由引理5和li(x)>0，i=1，2有

l2(x)tα-1≤(Lλx)(t)≤l1(x)tα-1，

(5)

因此Lλ：Q{0}→Q1，由引理9，可证谱半径r(Lλ)>0且Lλ有正特征函数ψ1，即

Lλψ1=r(Lλ)ψ1．

易得

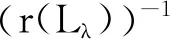
(6)

对∀x0∈Q{0}，设xn=A(xn-1)，n=1，2，…，假设x1-x0≠0(否则证明结束)，由(5)和(6)式有

则

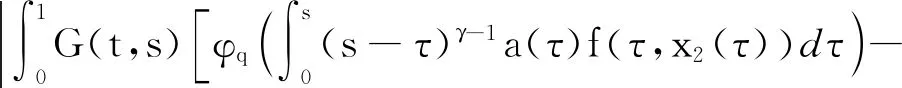
如此下去，有

n=1，2，…，

因此，对∀n，m∈Ν有

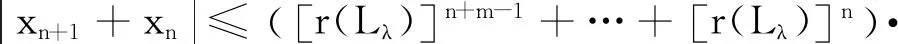
下证唯一性.

设z≠x*是A的非负不动点，则存在l1(|x*-z|)>0，使得

因此，

|Ax*-Az|=

类似上面的方法可以得到

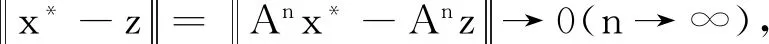
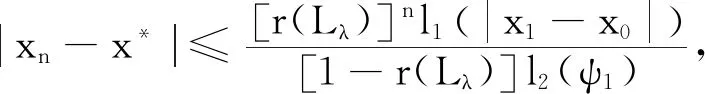
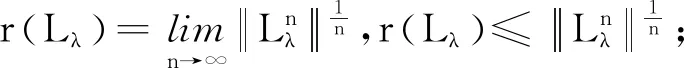
3 举例

考虑边值问题：

(7)

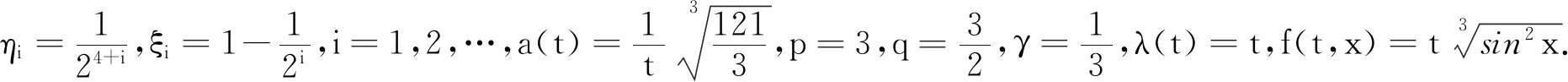
有

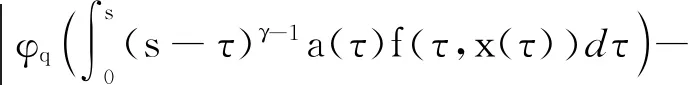
易得

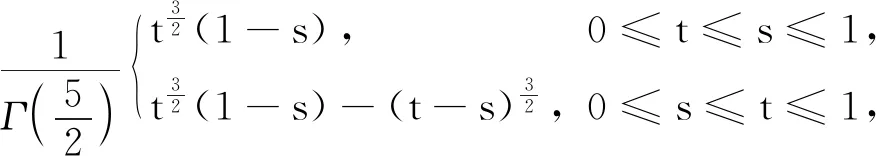
设

计算可得

故有

0.968<1.

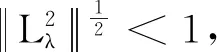
综上,满足定理1所需条件，故边值问题(7)有唯一正解．