从“蒲莞并生”再看《九章算术》中的“盈不足术”
郑硕,孙小淳
(中国科学院大学,北京100049)
“盈不足术”是我国古代一项非常重要的数学成就,它对世界数学的发展同样产生过重大影响[1]。在公元前二世纪初的数学书《算数书》中,就有通过“盈不足术”计算面积为一亩的正方形田地边长的记载[2]。中国传统数学经典《九章算术》中专门有一章介绍“盈不足术”的各种形式及其应用。将复杂的数学问题通过两次精巧的假设,转化成盈不足问题的形式,进而求解。这种以特定的数学模型来处理一大类应用问题的方法,正是中算家所擅长的[3]。
基于“盈不足术”这种“万能性”,数学史家在考察“盈不足术”时,倾向于把它描述成是一个可以不断扩展其运用范围的方法,“盈不足术”中蕴含的是一种“模型化”方法,可用于解决各种数学问题。这种乐观进步的编史学思路大体上也符合“盈不足术”的一般情况,但在一些特殊情况下,“盈不足术”在解题上的拓展就出现了问题。本文探讨的“蒲莞相生”问题,就属于这种情况。
“盈不足术”可以从线性问题拓展到非线性问题的求解,就是一个典型的编史学误读。钱宝琮认为,使用“盈不足术”求解一次函数问题时,这种解法是准确的;求解非一次函数时,得的数值是所求数的一个近似值[4]。李继闵也认为“盈不足术”解决问题给出线性问题的精确解和非线性问题的近似解[5]。白尚恕同样指出一次方程问题,以“盈不足术”计算,都得确切解,非一次方程问题,所得为近似解[6]。这里所谓“非线性问题”,指的是《九章算术》中的“蒲莞并生”“良驽相逢”“两鼠对穿”等问题。本研究以“蒲莞并生”问题为例进行分析。结果表明,“盈不足”章中的“蒲莞并生”问题并不是非线性问题,而是分段线性问题,所以使用“盈不足术”求解“蒲莞并生”问题得到的不是近似解,而是精确解。
本文对《九章算术》中使用“盈不足术”求解的二十个问题入手,对“盈不足术”的问题类型作出了划分,可以分为“一盈一不足”“两盈”“两不足”“一盈一适足”“一不足一适足”5种情形[7]。然后对“盈不足术”问题的拓展进行分析。当遇到“蒲莞并生”问题,原来“从线性问题”拓展到“非线性问题”的看法就成问题了。沈康身对“蒲莞并生”做出了正确的理解,用分段线性函数来描述蒲莞的生长,解决的还是非线性问题[8]。本文在此基础上,对这一问题做更加精细的解读,以求对“盈不足术”有更加深刻的理解。
1 《九章算术》中的“盈不足术”
《九章算术》成书于东汉(公元25年到220年)时期[9],是一部数学问题集,包括246个问题,并给出了解法。其中第七章叫“盈不足”,里面有20个问题,都是用“盈不足术”来解决。其中典型的是前4道题“今有共买物”“今有共买鸡”“今有共买琎”和“今有共买牛”。《九章算术》中的盈不足问题,
一般地可表示为下列“共买物”的数学模型[10]。
今有共买物,人出八,盈三;人出七,不足四。问:人数、物价各几何?
答曰:七人,物价五十三。[11]288
今有共买鸡,人出九,盈一十一;人出六,不足十六。问:人数、鸡价各几何?
答曰:九人,鸡价七十。[11]288
今有共买琎,人出半,盈四;人出少半,不足三。问:人数、琎价各几何?
答曰:四十二人,琎价十七。[11]288
今有共买牛,七家共出一百九十,不足三百三十;九家共出二百七十,盈三十。问:家数、牛价各几何?
答曰:一百二十六家,牛价三千七百五十。[11]289
《九章算术》给出的标准“盈不足”术文为:
置所出率,盈、不足各居其下。令维乘所出率,并以为实。并盈、不足为法。实如法而一。有分者,通之。盈不足相与同其买物者,置所出率,以少减多,余,以约法、实。实为物价,法为人数。其一术曰:并盈、不足为实。以所出率以少减多,余为法。实如法得一人。以所出率乘之,减盈、增不足即物价。[11]291-292
设两次付钱数(所出率)分别为a1和a2,盈(多余钱数)、不足(缺少钱数)分别为b1和b2。“置所出率,盈、不足各居其下”,即矩阵维乘”也即交叉相乘,“并以为实”就是将交叉相乘的结果相加a1b2+a2b1作被除数;“并盈、不足为法”是将盈数和不足数相加b1+b2作除数;“实如法而一”即就是“不盈不朒”时每人要出的钱数。
“置所出率,以少减多”是以两次假设人均出钱数a1和a2作差,|a1-a2|;“余,以约法、实。实为物价,法为人数”是以|a1-a2|为除数,将“实”a1b2+a2b1和“法”b1+b2代入算式;便得到物品价钱为和买家人数为将a1,a2,b1,b2代入算式,即得物品价钱和买家人数。“其一术”即另一种方法是用较大的“所出率”乘以人数需要“减盈”,以较小的“所出率”乘以人数则需要“增不足”。即物价同样可以求得物品价钱。
上述实际为“盈不足”问题的一般解法的代数表达。考虑到实际解题过程是一个试验值的过程,会出现“一盈一不足”型、“两盈”型、“两不足”型、“一盈一适足”型、“一不足一适足”型5种情形,分别对应于b1>0,b2>0;b1>0,b2<0;b1<0,b2>0;b1>0,b2=0;b1<0,b2=0的情况。《九章算术》对上述五种情况都给出了例题。“一盈一不足”型就是上面列举的第1题至第4题。
“两盈”型的例题是第5题“今有共买金”,“两不足”型的例题是第6题“今有共买羊”。
今有共买金,人出四百,盈三千四百;人出三百,盈一百。问:人数、金价各几何?
答曰:三十三人,金价九千八百。[11]294
今有共买羊,人出五,不足四十五;人出七,不足三。问:人数、羊价各几何?
答曰:二十一人,羊价一百五十。[11]294
对这两种情况《九章算术》给出的解法术文为:
两盈、两不足术曰:置所出率,盈、不足各居其下。令维乘所出率,以少减多,余为实。两盈、两不足以少减多,余为法。实如法而一。有分者,通之。两盈两不足相与同其买物者,置所出率,以少减多,余,以约法、实,实为物价,法为人数。其一术曰:置所出率,以少减多,余为法。两盈、两不足以少减多,余为实。实如法而一,得人数。以所出率乘之,减盈、增不足,即物价。[11]294-295
依据术文,可知解“两盈”“两不足”型问题的公式为

式(1)、(2)、(3)分别表示每人要出的钱数、物品价钱、买家人数。这三个公式实际就是针对两个特殊情况把上述典型的解式重新表达一下。
“一不足一适足”型的例题是第7题“今有共买犬”,“一盈一适足”型的例题是8题“今有共买豕”。
今有共买犬,人出五,不足九十;人出五十,适足。问:人数、犬价各几何?
答曰:二人,犬价一百。[11]297
今有共买豕,人出一百,盈一百;人出九十,适足。问:人数、豕价各几何?
答曰:一十人,豕价九百。[11]297
同样地,《九章算术》也给出了这两种类型问题的术文:
盈适足、不足适足术曰:以盈及不足之数为实。置所出率,以少减多,余为法。实如法得一人。其求物价者,以适足乘人数,得物价。[11]297
依据术文,可知解“一不足一适足”“一盈一适足”型问题的公式为

式(4)(5)分别表示物品价钱、买家人数。因为适足的正是人均出钱数,所以每人要出的钱数就是a2。因为在《九章算术》中并没有明确零的概念,本文表述使用的a1、a2、b1、b2均为正数,且都是以少减多。如果引入负数,用负的盈数表示不足,负的不足表示盈,再用零表示适足,那么,上述5种类型就可以统一化归到第1种类型即标准的“盈不足”公式求解。
2 “盈不足术”问题的拓展
上述8道例题中第1题至第4题即是标准的“一盈一不足”型问题,第5题至第8题分别是“两盈”型、“两不足”型、“一不足一适足”型、“一盈一适足”型问题。这8道题目都符合盈不足问题的基本形式,数理关系简单明了,都有明确的两次假设及相应的结果,依据术文即可方便求解,可以说是“盈不足术”的“范型”问题,亦可称作“盈不足术”的“本术”问题。本文认为这应是《九章算术》为拓展使用“盈不足术”所做的“模型”,为的是对号入座,将一般问题都划归为这5个“模型”解法。
通常求解数学问题的方法是依据题目中所给的数据,一步步推演得到结果。因为每一类问题有其特殊的思维过程,碰到新问题如果不得要领,新问题就如同“黑箱”。但对于一个一般的数学问题,先假设一个结果,代入题目中验算,肯定是盈、不足、适足三种情况之一。只需要通过两次假设,就可以把原来的问题划归为“盈不足”问题再进行求解,而无须考虑题目中纷繁的数量关系。就如“黑箱”,虽然不能观察其内部的系统状态,但只用分析其输入、输出变量,依然可以确定其结构参数。
《九章算术》“盈不足”章里接下来列举的12道例题,就是将一般的数学问题转化为标准“盈不足”问题来处理。即,虽然所举例题不符合“盈不足术”的“范型”问题的形式,但仍可利用两次假设将其划归为“盈不足术”的“本术”问题。钱宝琮主张非标准“盈不足”问题可分为四类“:互换”类,简单的比例问题(第9题、第15题);“合率”类,分工合作问题(第10题);“推解”类问题(第13题、第16题、第17题、第20题)“蒲莞”类问题(第11题、第12题、第19题);“方程”类,方程本术问题(第14题、第18题)[12]。这里分别列举说明:
“盈不足”章第15题。
今有漆三得油四,油四和漆五。今有漆三斗,欲令分以易油,还自和余漆。问:出漆、得油、和漆各几何?
答曰:出漆一斗一升四分升之一,得油一斗五升,和漆一斗八升四分升之三。[11]305
术曰:假令出漆九升,不足六升;令之出漆一斗二升,有余二升。[11]306
题意是知道3份漆可换得4份油,4份油可调和5份漆,现在有3斗漆,要用其中一部分换油,再用换来的油调和剩余的漆,问换油要多少漆,换得多少油,又调和了多少漆?按照术文,3斗就是30升,假设出9升漆,则可以换得12升油,调和15升漆,但30升漆出9升还余21升,15升漆有油可以调和,有6升漆没有油可以调,所以是不足6升;再假设出12升漆,则可以换得16升油,调和20升漆,但30升漆出12升还余18升,而所换得的油可以调和20升漆,所以是多余2升。代入盈不足公式得应出漆得油1升,和漆
“盈不足”章第10题。
今有垣高九尺。瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺。问:几何日相逢?瓜、瓠各长几何?
答曰:五日十七分日之五,瓜长三尺七寸一十七分寸之一,瓠长五尺二寸一十七分寸之一十六。[11]299
术曰:假令五日,不足五寸。令之六日,有余一尺二寸。[11]299
题意是知道有墙高9尺,瓜蔓自墙顶向下延伸,每日长7寸,葫芦自墙角向上生长,每日长1尺,问几日后两者相遇,各自长了多少?按照术文,假设5日瓜、瓠相遇,瓜蔓生长5日长度是3.5尺,葫芦生长5日长度是5尺,和9尺的墙相比少了5寸,这就是不足5寸;再假设6日瓜、瓠相遇,瓜蔓生长6日长度是4.2尺,葫芦生长6日长度是6尺,和9尺的墙相比多了1.2尺,所以有余1.2尺。代入盈不足公式得相遇日数日,瓜长度尺,亦即3尺寸,瓠长度亦即5尺寸。
“盈不足”章第13题。
今有醇酒一斗,直钱五十;行酒一斗,直钱一十。今将钱三十,得酒二斗。问:醇、行酒各得几何?
答曰:醇酒二升半,行酒一斗七升半。[11]303
术曰:假令醇酒五升,行酒一斗五升,有余一十;令之醇酒二升,行酒一斗八升,不足二。[11]303
题意是知道醇酒每斗值50钱,行酒每斗值10钱,用30钱买2斗酒,醇酒和行酒各买多少?按照术文,醇酒5钱1升,行酒1钱1升。假设买5升醇酒、15升行酒,那么总价是5×5+1×15=40钱,盈10钱;再假设买2升醇酒,18升行酒,总价是5×2+1×18=28钱,不足2钱。代入盈不足公式得升,即买醇酒升,买行酒升。
“盈不足”章第14题。
今有大器五、小器一,容三斛;大器一、小器五,容二斛。问:大、小器各容几何?
答曰:大器容二十四分斛之十三,小器容二十四分斛之七。[11]303
术曰:假令大器五斗,小器亦五斗,盈一十斗;令之大器五斗五升,小器二斗五升,不足二斗。[11]304
题意是知道5件大器,1件小器容量是3斛,1件大器,5件小器容量是2斛,问1件大器和1件小器容量各是多少?按照术文,3斛就是30斗,先设大器容量是5斗,根据已知条件一,则小器容量是30-5×5=5斗,推得1件大器,5件小器容量是30斗,较已知条件二余了10斗;再假设大器容量是5.5斗,按已知条件一得小器容量是30-5×5.5=2.5斗,推得1件大器,5件小器容量是18斗,较已知条件二不足2斗。代入“盈不足”公式得大器容量是斛,小器容量是亦即斛。
从以上几题可以看出,题目中的已知条件和问题之间的关系并不十分明显,甚至有些错综复杂,但并不妨碍使用两次巧妙的假设将题目转化为“盈不足”问题,然后套用公式进行求解,“盈不足术”的运用由此得到了拓展。
3 “蒲莞并生”问题对“盈不足术”拓展的性质
一般认为,用“盈不足术”解数学问题,只有在求解一元一次方程的问题时,才能求出精确解。以现代的代数式表示
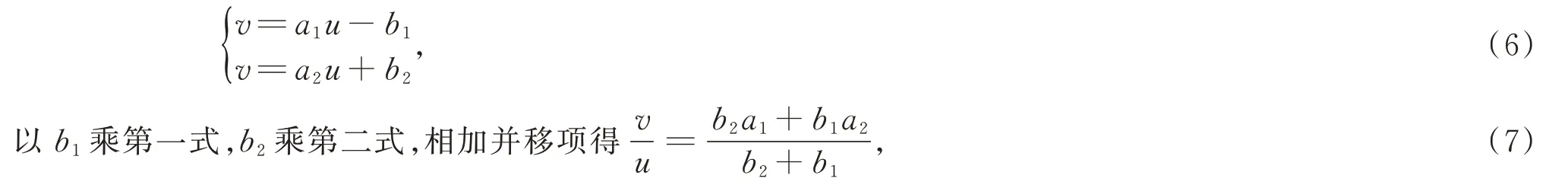
即如果假设x为所求的数,依照题目中所示的条件,通过两次假设,算出f(a1)=b1和f(a2)=-b2代入公式(7)得

很明显,如果问题属于线性问题,f(x)就是通过(a1,b1)和(a2,-b2)的直线,其与x轴的交点就是f(x)的根;而为非线性问题时,通过(a1,b1)和(a2,-b2)的直线与x轴的交点并不是f(x)的根,“盈不足术”实际上是一种线性插值的方法,这种解法得到的结果只可能是近似解。
且看“盈不足”章第11题“蒲莞并生”问题。
今有蒲生一日,长三尺;莞生一日,长一尺。蒲生日自半,莞生日自倍。问:几何日而长等?
答曰:二日十三分日之六,各长四尺八寸一十三分寸之六。[11]301
术曰:假令二日,不足一尺五寸;令之三日,有余一尺七寸半。[11]301
题意是知道蒲草第1日长高3尺,莞草第1日长高1尺,之后蒲草每日长高数是前一日的一半,而莞草是前一日的两倍,问两种植物多少日高度相等?按照术文,假设2日高度相等,则蒲草生长了4.5尺,莞草生长了3尺,相差1.5尺,所以是不足一尺五寸;再假设3日高度相等,则蒲草生长了5.25尺,莞草生长了7尺,超过1.75尺,这就是有余一尺七寸半。代入盈不足公式得长度相等日数日,各自高度尺,亦即4尺寸。

即这是一个指数方程,并非是一元一次方程,借助对数可求得x=log26≈2.59日,与“盈不足术”所得的解略有不同。这样理解,“盈不足术”看起来是拓展到了“非线性问题”的求解,只不过所得解为近似解。

然而实际情况并非如此。其实关于“蒲莞并生”问题,“蒲生日自半,莞生日自倍”意思蒲和莞每日都是等速率生长的。即蒲第1日生长速率恒为3,第2日生长速率恒为第3日生长速率恒为莞第1日生长速率恒为1,第2日生长速率恒为2,第3日生长速率恒为4……其累加生长高度图像是离散阶梯式的,并非是连续的光滑曲线,如图1所示。

图1 蒲莞累加生长高度折线图Fig.1 Line graph of cattail and bulrush accumulated growth height
所以“蒲莞并生”问题正确的解应该是
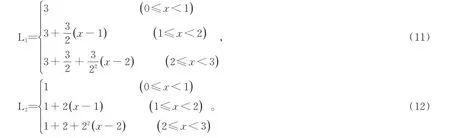
其中L1为蒲生长长度,L2为莞生长长度。蒲和莞应该在2<x<3时长度相等,列出方程1+2+22(x-2),解得日[8],因为在这一段是线性方程,所以按照盈不足术求解可以得到日的精确解。
沈康身还指出,对于等比级数和等差级数来讲,非正整数的项数在数学上是无意义的[8]。因此“蒲莞并生”问题根本不能用上述指数方程求解,需进一步分析。判断《九章算术》中问题的解题过程,不能仅依据“术曰”所说的方法。实际解题过程,应该比“术曰”所讲的更复杂,“术曰”很可能隐藏了一些中间的“试错”过程。
不妨来想象一下“试错”过程,分三种情况:
第一种情况:假令一日,不足两尺;令之二日,不足一尺五寸。这样这个问题就对应上述的“两不足”型问题,如第6题。照此求得的解为:
第二种情况:假令一日,不足两尺;令之三日,有余一尺七寸半。这同“术曰”一样,对应的是“一盈一不足”型问题,如第1题至第4题,但假设的天数不一样。答案是:
第三种情况:假令三日,有余一尺七寸半;令之四日,有余九尺三寸四分寸之三。对应的是“两盈”型问题,如第5题,则答案应该是:
上面三种假设情况应是在解题过程中可能出现的情况,但是得到的解与正确解大相径庭,问题就在于:在假设的区间内,蒲莞的高度变化根本不是线性的,而运用只能用于求解线性问题的“盈不足术”求解,当然会出问题。根据上面的数学式表述,“蒲莞并生”实际上是一个“分段线性问题”。《九章算术》“术曰”给出的解法,两个“假令”值已经处在其中一段线性区间,这时,问题已经变成了“线性问题”,解就在这个区间中,因而解是精确的。实际解题不可能一次就到这一步,前面可能的“试错”过程被隐藏了。
4 结语
《九章算术》中的“盈不足术”构造了解决一般数学问题的算法基础,在运用代数方法解决问题有困难时,这种利用两次假设与结果对比的“双设法”把表面非盈不足型问题划归为盈不足型问题然后再求解,为解决数学问题拓展了新思路。“盈不足术”是中国数学史上解应用问题的一种别开生面的创造,它在我国古代算法中占有相当重要的地位[13]。这种方法无疑是可以拓展到解决非线性问题的,但同时必须对非线性变化的细节有所分析。
本文分析的“蒲莞并生”问题,过去的研究者可能出于对“盈不足术”的自信,就直接认为《九章算术》已经把“盈不足术”拓展到非线性的问题解决了。但经仔细分析表明,“蒲莞并生”问题并不是严格的“非线性问题”,而是分段的“线性问题”。当试解值接近真值到一定区间时,在那个区间中就是“线性问题”,使用“盈不足术”求解的“蒲莞并生”问题仍然是线性问题,而并不是非线性问题。这样,对《九章算术》使用“盈不足术”解决问题的范围,就有了更加准确的认识。

