订正与会通：勾股定理在晚明《几何原本》（1607）中的呈现

潘澍原

（中国科学院 自然科学史研究所，北京100190）

晚明耶稣会士传教来华，欧洲学术随之输入，译介成书，刊布流播，获得相当程度的回应，其中最著名的是《几何原本》六卷。作为古典数学巨著《原本》（Elements）的汉文首译，《几何原本》往往被视作中西文明交流的象征。在其诸多内容中，勾股定理或最具代表性——它不仅是欧洲古典几何学中的经典命题，也密切关涉中国古代算学的重要畛域。本文将首先简述勾股定理的历史认知特别是在《原本》中的论证和后续传流，其次考察定理在《几何原本》等晚明西学著作中的译介概况，进而依据文本细节，重点分析相关内容如何通过翻译和校阅的具体实作呈现于《几何原本》之中，并讨论其背后的考量与认知，以期揭示晚明西学译介的某些重要特征，说明数学知识跨文化传播的复杂样态。

1 数学经典中的经典命题：勾股定理、《原本》及其传流

勾股定理揭示直角三角形的三边关系——斜边上的正方形面积等于两直角边上的正方形面积之和。这一关系简洁而深刻，相关认知可以上溯久远。古巴比伦时代的泥版文书就有不少涉及直角三角形斜边或矩形对角线的数学问题（至迟公元前17世纪），其富于范例性的解法已蕴含等价于定理内涵的一般性原则［1］。古印度吠陀经典《绳法经》（Śulbasūtras，至迟公元前6世纪）则明确表述，连接矩形对角的弦线造作的正方形面积是其长、宽两边各自造作的正方形面积之和，并据此进行图形的构造和变换［2-4］。至若中国古代，较早成书的《周髀》首章以边长3、4、5的直角三角形为例，通过一般性的图形分割移补解说三边关系；《九章算术》（约1世纪）则有一般直角三角形任知两边而推求余边的“句（勾）股术”及各类解直角三角形问题［5-6］①近年清理公布的秦简《数》（公元前212以前）有“圆材薶地”题，与《九章算术》“句股”章“圆材埋在壁中”题设问相近，数据、解答一致，其解法基于对勾股定理内涵关系的一般性认知，参见文献［7］。。就具体语境而言，这些认知尚不能视为定理，而是实施计算操作的“勾股法则”②Jens Høyrup在讨论古巴比伦时期的相关数学实作时强调，彼中并无定理，只有潜在的运算法则，参见文献［1］395－396，402。笔者以为，这一判断亦适用于古代印度和中国的相关认知，唯两者有明确乃至抽象的法则表述。。近世欧洲普遍将勾股定理的发现乃至论证归功于古希腊哲学家毕达哥拉斯（Pythagoras，约公元前570年至约公元前490年），而称以毕氏定理（Pythagorean theorem），其名延续至今，而其说难以确知①古典时代以降的学术叙事传统将毕达哥拉斯视为古希腊哲学和数学的重要奠基者，“毕氏定理”之名正是此传统延续至近代的一个体现。自19世纪中晚期开始，现代研究逐步怀疑以至否定此前归于毕氏本人的哲学思想和数学贡献。20世纪初，古典学家、希腊数学史家T.L.Heath面对相关证言年代过晚的质疑，仍以为尚无充分理据否认毕氏首先确立并论证勾股定理的传统，参见文献［8］351－352，［9］144－145。及至1960年代，古典学家W.Burkert通过其经典研究全面否认毕氏的数学家身份和数学贡献，学界由此形成基本共识；然亦有部分学者认为其论断过于苛刻，并推定毕氏对包括勾股定理在内的古希腊早期数学认知确有重要贡献。有关此一学术论争的述评，可参见文献［10］。。然则毕氏之后，古典时代的希腊学者确可能掌握勾股定理的知识内涵。譬如，在哲学家柏拉图（Plato，约公元前429年至公元前347年）的《美诺篇》（Meno）中，苏格拉底（Socrates）逐步引导美诺的仆人明了，面积倍于已知正方形的正方形须作于原形对角线之上，即指向定理在直角三角形等腰时的特例［9］297-298，［11］。

就今所知，勾股定理的一般性证明，首见于希腊化早期数学家欧几里得（Euclid，约公元前330年至约公元前260年）编纂的《原本》（约公元前300年）。该书13卷内容涵盖几何、数论、比例理论、不可分量等，广泛吸收希腊古典时代发展形成的数学知识，而以其基本、典要者为“原本”。这些知识以定义、公设、公理为基本原理（first principle），以定理和问题为命题的类型区分，以陈述、设定（setting-out）、目标（definition of goal）、作图、证明、结论等为命题的形式划分，通过综合方法，依据演绎逻辑编排命题次序，由此组织而成公理化体系。正缘于此，《原本》成为古希腊数学知识最为重要而集中的载体［12］。其书卷I讨论点、线、角、三角形、正方形、平行四边形等平面几何学的基础内容，卷中列述48道命题，由经逐步推证最终导向勾股定理及其逆定理，而两者又为其后多卷命题论证所倚赖②关于《原本》卷I的论证结构及勾股定理对其后诸卷命题论证的支撑，参见文献［13］。。因而，在《原本》的逻辑架构中，勾股定理享有关键地位。

《原本》卷I命题47陈述定理如下③据J.L.Heiberg编校希腊文本（1883）的Heath英译。：

在直角三角形中，对直角的边上的正方形等于夹直角的边上的正方形。［8］349

“对直角的边”即斜边，“夹直角的边”即两直角边，而其上正方形之“等”，即指面积相等④《原本》中表此意涵的“等”自卷I命题35出现，参见文献［8］327－328。。命题证明的核心是，自直角顶点作斜边之垂边的平行线，分斜边上正方形为两形，而各与两直角边上正方形等面积。简要言之（引征卷I命题及公理置黑括号内），如图1，设直角三角形ABC，角BAC为直角。先于边AB、AC、BC上各作正方形GB、HC、BDEC【命题46】。自点A作直线AL平行于BD和CE，连点作直线AD、FC。

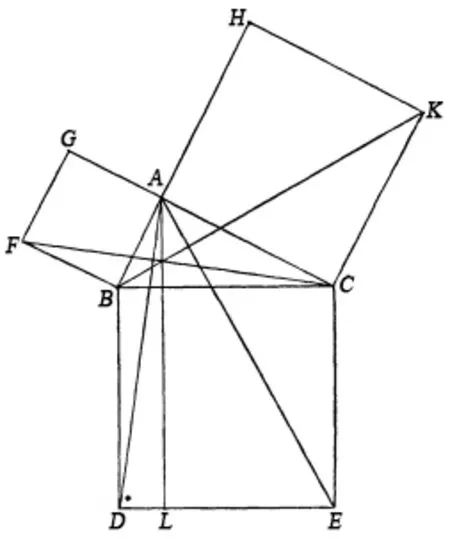
图1 《原本》中的勾股定理图示Fig.1 The diagram of Pythagorean theorem in the Elements

（1）三角形ABD和FBC中，边BC与BD等（正方形BDEC），边AB与FB等（正方形GB），角DBA与FBC等（直角DBC和FBA等，同加角ABC亦等【公理2】），故两形全等【命题4】。

（2）平行四边形BL和三角形ABD同以边BD为底，且同在平行线AL和BD内，故BL面积倍于ABD【命题41】。同理，正方形GB面积倍于三角形FBC（角BAC和BAG均为直角，故边CA与AG同线【命题14】）。

（3）由（1）（2），平行四边形BL与正方形GB等面积。同理，平行四边形CL与正方形HC等面积。即正方形BDEC面积等于正方形GB和HC面积之和【公理2】。

《原本》成书之后即为世所重，在古代晚期已称经典，中古时代输入阿拉伯世界，继而又回转欧洲，抄本众多，移译不绝，内嵌在其演绎结构中的勾股定理亦随之传流。另一方面，勾股定理本身也因其经典命题的价值得到专门的研究。一个值得指出的现象是，直角三角形等腰时的定理特例往往受到关注。例如，正因前揭《美诺篇》中苏格拉底式的证明仅针对等腰直角三角形，阿拉伯数学家塔比·伊本·库拉（Thābit ibn Qurra，836—901）才应友人的请求将其一般化［14］。又如，作为《原本》在文艺复兴时期最具影响的两个拉丁文排印本，1482年坎帕努斯（Campanus of Novara，约1220—1296）译本和1505年赞贝蒂（Bartolomeo Zamberti，1473—1543）译本的相应命题均以等腰直角三角形为图［15-16］；1516年双译合编本的坎氏、赞氏题图则分别为等腰和非等腰形式（图2）［17］。在同时期意大利学者瓦拉（Giorgio Valla，1447—1500）百科式的遗著（1501）中，定理的证明遵从《原本》，却各就等腰和非等腰直角三角形给出两种图示，申说部分还专门讨论等腰情形并附相应图解（图3）［18］。

图2 坎帕努斯—赞贝蒂双译合编本《原本》中的勾股定理Fig.2 The Pythagorean Theorem in the First Conjunction of Campanus’s and Zamberti’s Translations of the Elements

图3 瓦拉《关于追求与避免之事的著作》中的勾股定理Fig.3 The Pythagorean Theorem in Giorgio Valla’s De expetendiset fugiendisrebusopus

2 勾股定理在晚明的译介：《几何原本》及其他

《几何原本》在晚明的翻译和出版，成为勾股定理自欧洲传入中国的自然路径。这部西学经典的问世，有赖耶稣会士利玛窦（Matteo Ricci，1552—1610）和亲教士人徐光启（1562—1633）的精诚合作。利玛窦于万历十年（1582）航抵澳门，进入内地后逐步采取“适应政策”传教，尤积极结交士宦显贵等社会上层，以讲谈著述构建自身的“西儒”形象。万历十九年（1591）开始，利氏在韶州、南京等地数度向士人指授《原本》的部分内容，并与瞿汝夔（1549—1612）初译其第一卷。万历二十八年末（1601），利氏入都贡献，获准留居。徐光启则于万历三十二年（1604）会试中第，馆选在京，得与利氏长相过从，商量问学。万历三十四年（1606）秋，利、徐二人谈论欧洲学术，语及《原本》之精要，遂据利氏业师丁先生（Christoph Clavius，1538—1612）编注本合译其书；次年（1607）春，前六卷译毕刊行①《几何原本》翻译成书及刊印的详细经过，参见文献［19］。。

丁先生是耶稣会早期最为杰出和权威的数学家和天文学家，长期任教于该会罗马学院（Collegio Romano），大力倡导、推行数学教育，为此订立课纲，编撰教材，影响广远，尤以多次修订再版的《欧几里得原本十五卷》（Euclidis Elementorum libri XV）闻名②丁氏的生平和著述，参见文献［20-22］。。该书并非普通意义上希腊文本的翻译，而是包含大量注解——既有先前诸家的集解，也有丁氏自己的阐释和评论，命题的证明也往往重加撰述以使其更为清晰显明，便于理解［8］105。利玛窦早年在罗马学院研修四年有余（1572—1577），尝从丁先生受学，研习以《原本》为基础的“数学科学”［23］，［24］54-58，嗣后入华传教，业师著作正是译撰西学的当然之选。《几何原本》第一卷“求作”（公设）、“公论”（公理）及各卷“界说”（定义）的数量与安排，是其书出自丁氏编注本1574年初版的明证［24］137-138；诸命题除可与欧几里得原书对应的内容以外，亦时有“增”“注”“用法”等，具体表现出丁氏纂辑与注解的风貌。

《几何原本》所译勾股定理即第一卷第四十七题，命题陈述与对应的丁氏《欧几里得原本十五卷》卷I命题47陈述原文分别作：

凡三边直角形，对直角边上所作直角方形与余两边上所作两直角方形并等。［25］41a

In rectangulis triangulis，quadratum，quod a latere rectum angulum subtendente describitur，aequale est eis，quae a lateribus rectum angulum continentibus.［26］72r

比照前揭《原本》陈述，丁氏文本的句式、意涵皆同。汉译“对直角边”沿用拉丁原文的指示方式，表意准确，相对该边而称的“余两边”则代指原文“夹直角的边”（lateribus rectum angulum continentibus）；全句以“凡”起首，强调定理对于任意直角三角形均成立①事实上，“凡”系《几何原本》定义、定理陈述的常用词，以增强表述的一般性，参见文献［24］165。，由此完全表达出原文“在直角三角形中”（In rectangulis triangulis）而“直角三角形”为复数的准确内涵。《几何原本》中的陈述虽未严格依照底本译出，亦可谓尽传原意，简明确当。至于证明，汉译文本也基本按原有方式展开明晰的论述。

《几何原本》而外，勾股定理亦见于晚明西学著作《大测》（1630）和《测量全义》（1631），但两书皆只简单述及题旨，而未予严格证明。《大测》系崇祯初年明廷开局修历、引用西法之际耶稣会士邓玉函（Johann Terrenz，1576—1630）等编译的三角学专论，卷首“因明篇”将勾股定理作为平面三角学的基础知识列出：

直角旁之两腰，其能与弦等。能等者，谓两腰上两方形并与弦上方形等也。《几何》一卷之四七②邓玉函：《大测》卷1，崇祯三年（1630）刊崇祯历书本，6a。。

句尾小注明确标示征引《几何原本》中的勾股定理，然则陈述方式颇异：所举正方形相等关系，先及直角边而后斜边；“直角旁之两腰”的称法与《原本》“夹直角的边”近似，且以斜边为底而指称为“腰”；更直接以特殊名称“弦”代指对直角的斜边③又，《大测》陈述勾股定理所用之“能”，或承自《几何原本》第二卷第一题“注”中所称“二卷前十题皆言线之能也”，其下注文云“能者，谓其上能为直角形也”。。稍后成书的《测量全义》由耶稣会士罗雅谷（Giacomo Rho，1593—1638）、汤若望（Johann Adam Schall von Bell，1592—1666）等译撰，全面论述欧洲实用几何知识④《测量全义》题名之“测量”实指欧洲数学传统中的“实用几何”（practical geometry），参见文献［27］470脚注②。关于此点，仍将另文详为阐论。，第五卷“测面下”有“变形法”，其五“两正方形变为一正方”，题注曰“《几何原本》一卷四十七题备论其理，此则用法”⑤罗雅谷，龙华民，汤若望等：《测量全义》卷5，崇祯四年（1631）刊顺治二年（1665）重修西洋新法历书本，27a。，说明该题只是以《几何原本》所论勾股定理为理据的图形变换方法⑥既往研究多以此题为勾股定理证明之另法，参见文献［6］15。其欧洲源流及相关讨论拟别作阐述，此不赘。。题中令两正方形边相接互成直角，以此构造直角三角形，其斜边联结两正方形各一角，

即以为底，作正方形，其积与两元形并积等⑦罗雅谷，龙华民，汤若望等：《测量全义》卷5，崇祯四年（1631）刊顺治二年（1665）重修西洋新法历书本，27a。。

相较《几何原本》，这一表述直截地将一形与两形并“等”实为面积相等的含义显明出来。

3 剜字而存图：利玛窦、徐光启对勾股定理一般性的理解和处理

前已述及，勾股定理在汉译文本中的论证依循《原本》而明晰无误，不过相关文本的具体内容和样态仍值得进一步讨论。《几何原本》中的定理在陈述之后一般分为“解”“论”两部分，前者包含命题的设定和目标，后者则是证明及辅助作图［24］162。第一卷第四十七题之“论”首叙作图：“试从甲作甲癸直线与乙戊、丙丁平行，本篇卅一。分乙丙边于子。”［25］41b其后半句明刊本原作“ 分乙丙边于子”，留有两字阙空（图4）⑧纪志刚2012年校点《几何原本》第一卷时首先发现此阙，并在上海交通大学数学史讨论班上初步分析其学术内涵。其后笔者考阅十数种明刊《几何原本》，包括已知刊印最早的中国国家图书馆藏韩应陛题跋本（馆藏著录为万历三十五年（1607）初刊本）在内的所有印本均有此阙。。同样引人注意的是，命题图示列有两幅，分别表现直角三角形等腰和非等腰情形（图4），却未见相关说明。明刊阙空原系何字，又何故剜去？题图何以同时列示两种情形，其中有何意蕴？

图4 《几何原本》明刊本中的勾股定理Fig.4 The Pythagorean theorem in Jiheyuanben，Ming edition

欲讨论这些问题，必须在底本和译本之间比对考析勾股定理除前揭命题陈述以外的全部内容。首先，题图以等腰、非等腰两种形式并举，为丁氏编注本所原有（图5）［26］72r，利玛窦和徐光启在汉译时照样沿用。次将拉丁文本和文言文本具录如下，以相同字母—数字对应编号，以下划线标识主要差异。

图5 丁氏《欧几里得原本十五卷》（1574）中的勾股定理Fig.5 The Pythagorean theorem in Clavius’s Euclidis Elementorumlibri XV（1574）

［S］In trianguloABC，angulusBAC，sit rectus，describanturque superAB，AC，BC，quadrataABFG，ACHI，BCDE.［G］Dico quadratumBCDE，descriptum super latusBC，quod angulo recto opponit，aequale esse duobus quadratisABFG，ACHI，quae super alia duo latera sunt descripta，siue haec duo latera aequalia sint，siue inaequalia.［P1］Ducatur enim rectaAK，parallela ipsiBE，vel ipsiCD，secansBC，inL&iungantur rectaeAD，AE，CF，BH.［P2-1］Et quia duo anguliBAC，&BAG，sunt recti，erunt rectaeGA，AC，vna linea recta；［P2-2］eodemque modoIA，AB，vna recta linea erunt.［P3-1］Rursus quia anguliABF，CBE，sunt aequales，cum sint recti，si addatur communis angulusABC，fiet totus angulusCBF，toti anguloABE，aequalis；［P3-2］similiterque totus angulusBCH，toti anguloACD.［P4-1］Quoniam igitur lateraAB，BE，trianguliABE，aequalia sunt lateribusFB，BC，trianguliFBC，vtrumque vtrique，vt constat ex definitione quadrati；［P4-2］Sunt autem&anguliABE，FBC，contenti hisce lateribus aequales，vt ostendimus；［P4-3］Erunt triangulaABE，ABCaequalia.［P5-1］Est autem quadratum，seu parallelogrammumABFG，duplum trianguliFBC，cum sint inter parallelasBF，CG，&super eandem basinBF；［P5-2］Et parallelogrammumBEKL，duplum trianguliABE，quod sint inter parallelasBE，AK，&super eandem basinBE.［P6-1］Quare aequalia erunt quadratumABFG，¶llelogrammumBEKL；［P6-2］Eadem ratione ostendetur，aequalia esse quadratumACHI，¶llelogrammumCDKL.［P6-3］Erunt enim rursus triangulaACD，HCB，aequalia，ideoque eorum dupla，parallelogrammum videlicetCDKL，&quadratumACHI.［P7］Quamobrem totum quadratumBCDE，quod componitur ex duobus parallelogrammisBEKL，CDKL，aequale est duobus quadratisABFG，ACHI.［C］In rectangulis ergo triangulis，quadratum&c.Quod demonstrandum erat.［26］72r-72v

解曰：［S］甲乙丙角形，于对乙甲丙直角之乙丙边上作乙丙丁戊直角方形。本篇四六。［G］题言，此形与甲乙边上所作甲乙己庚及甲丙边上所作甲丙辛壬两直角方形并等。

论曰：［P1］试从甲作甲癸直线与乙戊、丙丁平行，本篇卅一。 分乙丙边于子。次自甲至丁、至戊各作直线。末自乙至辛、自丙至己各作直线。［P2-1］其乙甲丙与乙甲庚既皆直角，即庚甲、甲丙是一直线。本篇十四。［P2-2］依显乙甲、甲壬亦一直线。［P3-1］又丙乙戊与甲乙己既皆直角，而每加一甲乙丙角，即甲乙戊与丙乙己两角亦等。公论二。［P3-2］依显甲丙丁与乙丙辛两角亦等。［P4-1］又甲乙戊角形之甲乙、乙戊两边，与丙乙己角形之己乙、乙丙两边等，［P4-2］甲乙戊与丙乙己两角复等，则对等角之甲戊与丙己两边亦等，［P4-3］而此两角形亦等矣。本篇四。［P5-1］夫甲乙己庚直角方形倍大于同乙己底、同在平行线内之丙乙己角形，本篇四一。［P5-2］而乙戊癸子直角形亦倍大于同乙戊底、同在平行线内之甲乙戊角形，［P6-1］则甲乙己庚不与乙戊癸子等乎？公论六。［P6-2］依显甲丙辛壬直角方形与丙丁癸子直角形等。［P7］则乙戊丁丙一形与甲乙己庚、甲丙辛壬两形并等矣。［25］41b-42a

比勘表明，底本与译本的文本内容大体一致。译本在具体表述上或稍有改易，如前引“试从甲作甲癸直线与乙戊、丙丁平行，分乙丙边于子”，在如实表达底本［P1］“Ducatur enim rectaAK，parallela ipsiBE，vel ipsiCD，secansBC，inL”之外，又增“从甲”二字。更显著的差异是，某些底本语段在译本中略而未表。其中，［P4-1］［P4-2］句尾是其述论依据的简略说明，［P6-3］是前句“同理所示”（Eadem ratione ostendetur）的理据概要，［C］重申题旨以为结论①《几何原本》全书均未继承这一结论形式，参见文献［24］162。，或显而易见，或述意重复，皆非紧要，而［G］后半句则别有意趣。经简化、转换、重组等方式，底本［S］［G］即命题设定和目标的主要内涵在“解”中得以等价表达，唯最后的补充说明“这两边或等或不等”（siue haec duo latera aequalia sint，siue inaequalia）未予译出——所谓“这两边”，是指相对于“对直角的边BC”（latusBC，quod angulo recto opponit）而言的“另两边”（alia duo latera），亦即直角边AB、AC。这一说明不见于欧氏原书［8］349-350，而题图的两种形式显然与之呼应②同时期的《原本》权威版本康曼迪诺（Federico Commandino，1509—1575）译注本亦无类似表述，其图示直角三角形非等腰，见文献［28］。③纪志刚2016年8月通览本文原稿后指出，勾股定理图示的等腰形式应当渊源有自，并给出数例，笔者就此追溯查考，特此致谢。。丁氏在编译《原本》时广稽群书，必当阅及勾股定理的两种图示及其等腰情形的有关论说，故而将两种图示兼收并取，同时在申述目标时阐明其不论直角三角形等腰与否皆成立，强调命题的一般性。汉译在“题言”中未及丁氏补说之意，固然无可厚非，却使得两幅图示缺乏应有的文本照应。

复次，明刊本阙空也与两种图示的配置紧密关联。事实上，直角三角形是否等腰与其斜边是否平分相应。由以上考察推测，阙处原文当是“而平”二字④清人校勘《几何原本》时已有同样或类似意见，典型者如光绪间刘铎纂辑《古今算学丛书》，依明刊本留阙，卷末校记称“‘分乙丙’上原空二格，疑是‘两平’二字，后挖去”（利玛窦，徐光启：《几何原本》卷1，光绪二十四年（1894）石印古今算学丛书本，52a，54b）。另《四库全书》文渊阁本改前句注文“本篇卅一”双行为单行以补阙空（卷1，54a），道光丁未（1847）海山仙馆刊本以“而平”二字补阙（卷1，48a），同治四年（1865）金陵书局刊本则仅补“而”一字（卷1，41b），此三种版本差异亦为纪志刚所发现。，原句即“试从甲作甲癸直线与乙戊、丙丁平行，而平分乙丙边于子”。可以推想，利玛窦和徐光启初译此题时，或受到前图直角三角形等腰的影响，不自觉地将甲癸直线平分乙丙边的特定图式写入译稿。待其书刊版初印以后，利、徐二人在校阅时察觉到“平分乙丙边”的表述有碍作图结果的一般性，而后续论证亦与甲癸如何切分乙丙边无关，遂将“而平”剜去⑤实际上，明刊《几何原本》为校正原有瑕疵而经剜版留阙者非此一处，它们既是汉译文本呈现过程的重要一环，也是相关知识传播和理解的特殊见证。，却仍保留前图的等腰形式⑥值得指出的是，命题在翻译过程中另有一项校正：底本［P2－1］因角BAC和角BAG均为直角而判定直线GA、AC系同一直线，边注征引“4.primi.”即卷I命题4，实际当引命题14，而汉译相应文句“其乙甲丙与乙甲庚既皆直角，即庚甲、甲丙是一直线”的注文改正作“本篇十四”。。从翻译和校阅的具体实作考量，利、徐沿用底本兼列直角三角形等腰和非等腰情形的图示，虽略去相应的文本说明，仍不失为一种对命题一般性的隐性表达。

4 会通中西：徐光启对勾股定理丁氏注解附题的理会与译解

完整述论勾股定理之余，《几何原本》第一卷第四十七题还附有四道增设命题［25］42a-44b。查对底本可知，原题注解（scholion）部分附有丁氏收集的相关命题8道，《几何原本》所附者乃自其第1、第4、第6、第8题移译（表1）。“一增”陈述的“凡直角方形之对角线上作直角方形，倍大于元形”，即适用于等腰直角三角形的定理特殊形式，丁氏将此特例列为首题，正是对其学术传统的一种回应，而利玛窦和徐光启亦予采纳。“二增题”“三增题”则是利用定理的作图，前者以两不等直角三角形化为并积不变的两相等直角三角形，后者以多矩形并为一矩形，正是欧洲几何学图形变换流播中国的早期实例。

表1 明译《几何原本》勾股定理所附增设命题陈述及对应底本注解原文Tab.1 The enunciations of the added propositions appended to the Pythagorean theorem in the Chinese translation of the Elements and the corresponding paragraphs in the sourcebook

至于“四增”则尤为令人瞩目①安国风曾对此“四增”作简要分析，参见文献［24］244－245。。其题曰：

三边直角形，以两边求第三边长短之数。

法曰：甲乙丙角形，甲为直角，先得甲乙、甲丙两边长短之数，如甲乙六，甲丙八，求乙丙边长短之数。其甲乙、甲丙上所作两直角方形并既与乙丙上所作直角方形等，本题。则甲乙之幂自乘之数曰幂得三十六，甲丙之幂得六十四，并之得百，而乙丙之幂亦百。百开方得十，即乙丙数十也。又设先得甲乙、乙丙，如甲乙六，乙丙十，而求甲丙之数。其甲乙、甲丙上两直角方形并既与乙丙上直角方形等，则甲乙之幂得三十六，乙丙之幂得百，百减三十六，得甲丙之幂六十四。六十四开方得八，即甲丙八也。求甲乙仿此。 此以开方尽实者为例，其不尽实者，自具算家分法。［25］44a-44b

此题旨趣，实与中国古代算学之“句股术”差相仿佛，即“句、股各自乘，并而开方除之，即弦”，“句自乘，以减弦自乘，其余开方除之，即股”等［29］。不过，其“法”仍是基于“甲乙、甲丙上所作两直角方形并既与乙丙上所作直角方形等”这样具体应用勾股定理的几何观点予以解说和计算，与作为算法程序的“句股术”及其求解仍有相当的差别②应予提及的是，此“四增”后收入耶稣会士艾儒略（Giulio Aleni，1582—1649）、瞿式穀（1593—1645以后）编译之《几何要法》（1631）卷三“有三边直角形以两边求第三边长短之数章第十四”，而略去尾句，改夹注“本题”为“《原本》卷一四十七”（艾儒略，瞿式穀：《几何要法》卷3，崇祯四年（1631）序闽中景教堂刊本，7b－8b）。又前揭《大测》“因明篇”陈述勾股定理后亦称，“此理之用，为先得二边以求第三边”（邓玉函：《大测》卷1，崇祯三年（1630）刊崇祯历书本，6a），其后具例求解，亦与此“四增”略同。。

为作进一步考察，引述底本丁氏注解附题VIII如下（今译文置花括号内）：

Cognitis duobus lateribus quibuscunque trianguli rectanguli，in cognitionem reliqui lateris peruenire.

Sit angulusA，rectus in trianguloABCsintque primo cognita lateraAB，AC，circa angulum rectum，quorumAB，ponatur 6 palmorum，&AC，8.Quoniam igitur quadrata rectarumAB，AC，nempe palmi 36&64 aequalia sunt quadrato rectaeBC；Si illa coniungantur simul，efficietur hoc palmorum 100.Latus ergoBC，continebit 10 palmos.Tantum enim est latus，seu radix quadrata 100 palmorum，vt perspicuum est apud Arithmeticos.Sint secundo cognita lateraAB，BC，sitqueAB，6 palmorum，&BC，10.Quoniam igitur quadrata rectarumAB，AC，aequalia sunt quadrato rectaeBC；Si quadratum rectaeAB，quod continet palmos 36 detrahatur ex quadrato rectaeBC，quod est palmorum 100，remanebit quadratum rectaeAC，64 palmorum.Latus ergoAC，continebit 8 palmos.Tanta enim est radix quadrata，seu latus 64 palmorum.Quod est propositum.Caeterum non semper hac arte inuenientur numeri rationales，quia non omnes numeri habent latus，radicemve quadratam，vt notum est apud Arithmeticos；Vnde latus inuentum saepe numero exprimi nequit，nisi per radicem surdam，quam vocant：Sed de his alias.［26］75r-75v

｛已知直角三角形的任意两边，以求知剩余一边。｝

{设角A是三角形ABC中的直角，且首先已知直角边AB、AC，其中AB设定为6掌宽的，而AC（设定为）8（掌宽的）。既然直线AB、AC的平方，也就是36掌宽和64掌宽，等于直线BC的平方；如果它们相加，这将得出100掌宽。故边BC将有10掌宽。边确实是如此大小，即100掌宽的平方根，正如算术家明了的。其次已知边AB、BC，且AB为6掌宽的，而BC（为）10（掌宽的）。既然直线AB、AC的平方等于直线BC的平方；如果直线AB的平方——那有36掌宽，从直线BC的平方——那是100掌宽的——中减去，将余下直线AC的平方64掌宽。故边AC将有8掌宽。平方根确实是如此大小，即64掌宽的边。这就是命题的要求。另外，由此方法不总是求得有理数，因为并非每个数都有边，或者说平方根，正如算术家知道的；因而所求边往往不能用一个数而只能用所谓的不尽根表示。然此另当别论。}

丁氏注解附题VIII在述论风格上类于命题中的问题，而“四增”求解部分所冠“法曰”一词，正是《几何原本》专用于问题的形式术语［24］162。“四增”的设例用数、求解方式等多与底本一致，而添注引证“本题”，则有意强调其解法以勾股定理为依据。不过，相较丁氏底本的表述，汉译文本的算法特征更为突出。如底本的问题陈述仅是“求知剩余一边”，汉译则明言所求为第三边的“长短之数”①一般而言，中国古代算学中的“数”，指一般量而非数量。。虽则丁氏在具体述论中对正方形边长赋值并展开运算，但其具体量值均为带单位的度量——“掌宽”（palmus）即欧洲文艺复兴时期承用的罗马长度单位名称，而汉译将此等单位尽皆省去②此细节承林力娜（Karine Chemla）2019年7月审阅文稿时向笔者点出，特此致谢。，只以纯粹的数量演示运算。

更富意趣的是，汉译文本中出现诸如“甲乙之幂”等表示某边之上正方形面积的称法，并注曰“自乘之数曰幂”，又有“开方尽实”“不尽实”等语，均采用中国古代算学术语，而原文的“Arithmeticos”亦被转译为富于传统意味的“算家”。这些译语显系徐光启之手笔，既反映出他对勾股、开方等中算知识的了解乃至稔熟，也表现出他对欧洲传华知识的理会和接纳。面对丁氏注解中引入具体算例的问题，徐氏并未以内涵相近的“句股术”③在徐光启所能阅及的宋元以降特别是明代流行的算书中，“句股术”多以具体的某某“法曰”或“术曰”表述。代言其义，却又在翻译过程中自觉或不自觉地借用中算术语组织表述，在潜移默化之间会通旧学与新知，而这亦生动展现出本土固有的学术语境在外来知识受容过程中隐微的涵化（acculturation）作用。

5 结语

《几何原本》无疑是徐光启西学译介的开端，而由其督修的历算大典《崇祯历书》可算作终点。正是在《崇祯历书》的规划纲要中，徐氏提出“欲求超胜，必须会通；会通之前，先须翻译”［30］347的历法修改方针。这一超卓的识断屡为近世论者所激赏，而学界亦多就其说，将明清之际学术知识自欧洲的传入、介绍和翻译与中国学者的研习、接纳和会通，视为两个前后接续的过程。例如，徐氏在《几何原本》译成之后为中算传统的勾股知识补作论证的《句股义》，就被视为中西会通的代表著作。

然而，通过审读、比勘和分析《几何原本》第一卷第四十七题及其拉丁底本的相应内容，可以对此等观念稍加检讨。诚如所见，利玛窦和徐光启翻译及至最终呈现勾股定理的过程，显然不是从拉丁文本到文言文本的简单语义转换，其间既有对作图叙述的修正，也有对古算术语的借用，而相关的学习与讨论、理解与考量亦深蕴其中，形成更为丰富的内涵。作为积极译介西学的知识实践者，利玛窦和徐光启在翻译、校阅过程中对文本谬误的订正和对关联知识的会通，或是主动之举，或是潜意而为，而这些实作都渗透着他们理解不同文化中的数学知识的努力和热忱。藉此考察，我们亦得以从微观角度理解数学知识的跨文化传播何以成为可能。

后记并致谢：本文的核心内容和思路2016年首揭于笔者博士学位论文，时匆遽成稿，未遑深论。2016年8月承硕士导师纪志刚教授通览原稿并予具体意见，因此复作相关考索，订补前论。2019年7月修订稿又承林力娜（Karine Chemla）研究员细致审读，批点指要，助益良多。2020年重修新稿，期间数就疑难咨问Jens Høyrup教授及学兄郑方磊博士，每得解惑。教益种种，谨申谢忱。