从形式到方法：徐有壬“缀术”的双重意义

王鑫义，郭世荣

（内蒙古师范大学 科学技术史研究院，内蒙古 呼和浩特010022）

徐有壬（1800—1860），字君青（钧卿），浙江乌程（今湖州市）人，晚清八大算学家之一［1］。他所著的《测圆密率》三卷（1840年前后）是在没有受西方近代数学影响之下独立研究的结果，共有56“术”，每“术”即为一个公式。《割圆八线缀术》（以下称“《缀术》”）则是他的代表作，原作三卷，后由吴嘉善（1820—1885）述草（1862）和左潜（？—1874）补草（1873）为四卷，该书包括了《测圆密率》中全部的级数展开式，并创造了推求级数展开式的“缀术”。

关于徐有壬的《测圆密率》和《割圆八线缀术》，李俨［2］、钱宝琮［3］、李迪［4］、王海林［5］、孙力［6］、罗见今［7－8］和张升［9］等对此有过详尽分析，各有侧重，但对“缀术”的中算来源只有一些零星讨论，忽略了“缀术”作为运算方法这层意义，且对“因式立术，由术立法”的实质阐述不多。鉴于此，本文以徐氏《测圆密率》和《割圆八线缀术》为研究对象，对相关问题做进一步的考察和分析。

1 “缀术”表达级数的中算来源

清代数学家真正全面掌握天元术是从李锐（1769—1817）完全读懂《测圆海镜》开始的。此后，清代中后期的数学家对天元术和借根方都很熟悉，对二者关系的认识也逐渐深入［10］。

1.1 天元、四元术的影响

1822年，徐有壬首次读到《四元玉鉴》钞本后，“积思三昼夜，写出细草”［11］，他未刻的《四元算式》是对《四元玉鉴》的细草，也是清代研究《四元玉鉴》最早的著作。黎应南在《演元九式》序中称“徐有壬甄而明之，使读者有下手处”［12］，认为徐氏通晓并帮助读者理解四元术。徐有壬对《四元玉鉴》的深入研究，为以后罗士琳（1789—1853）的细草和其他人的注释起了重要作用［5］12，从徐氏给罗士琳《演元九式》（1827年）的序中也可看出，他是完全理解四元术的数学含义及相消方法的［13］。此外，徐氏曾将《四元玉鉴》3册寄赠朝鲜学者金正喜［14］；沈钦裴（《四元玉鉴细草》三卷，1829年）、罗士琳（《四元玉鉴细草》三卷，1835年）对四元术的理解也都受到了徐氏的影响。可以说，徐有壬为四元术于清代被重新理解的关键人物［13］45。

徐有壬在研究《四元玉鉴》的基础上，对垛积招差之法最有心得，而其《造各表简法》（又称为《垛积招差》）早在1856年已经写成［15］。他在《造各表简法》的序中写道：“余读《四元玉鉴》，究心于垛积招差之法，推之割圆诸术，无所不通。”［16］事实上，徐有壬研究割圆术比戴煦和李善兰都早，并把垛积招差二法运用到了割圆问题中。

1.2 对天元术、借根方和代数学的理解

1859年，冯桂芬与徐有壬一起研究《代微积拾级》，徐有壬认为：“是法壬叔外鲜能通晓，书中文义语气多仍西人之旧，奥涩不可读，惟图式皆可授，宜以意紬绎图式，其理自见。”［17］表明他对李善兰等的翻译工作并非全然接受。在《缀术》中，徐氏比较了代数学与天元术。可见，徐有壬未用代数学，一是表达的不便性；二是运算的繁琐性；三是深谙天元术的本质，并非完全的泥古不化；但与中西两种文化固有的观念和方法不无关系。

需要注意的是，徐有壬同时掌握借根方，深谙天元术，又接触过代数学。他在研究《四元玉鉴》并为之补细草时强调天元术的重要性与实用性，在《缀术》中则与左潜都表明天元术优于借根方，并把“缀术”视为天元术的变形，而在读到《代微积拾级》时，又指出其佶屈聱牙、晦涩难懂。这些不同阶段的观点反映了他研究天元术、借根方与代数学的动机与动力的不同，不只反映了天元术与代数学这两种主流学术传统的竞争与比较的过程。天元术、四元术与借根方对理解代数学起了很大作用，反过来，西方代数学也是帮助理解天元术、四元术和借根方的重要工具。

2 算式、率式和级数式的说明

2.1 构成要素

算式由三部分构成：率名（即连比例各率，用一、二、三等表示率名）、率数（即分子或乘数，用商业暗码〡、〢、〣、〤、〥等表示）和除法（即分母用小字旁书寄于率上）。

对于“率式”，在“比例法”中有所说明：“比例既毕，乃取各式之四行齐等列而相并，得数重列之，为所求各率式也。”［18］所谓“各率式”是指用“比例法”求得的每行率式，“算式”仅指其中的一部分，实指单项式，而“各率式”是多项式或是多个单项式的和。由于这些“算式”共存于一式即“率式”，各项之间构成连比例，因此，对于“率式”也可以按各算式的相关规则去运算。

对于“级数式”，徐有壬先在《缀术》卷二中引入了“级数”：“新译西算所云‘级数’是也，其求法初若繁重，究之得数级后，其余‘级数’可以推类，而得以等级井然也。”［18］由此说明：一方面徐有壬已见到《代微积拾级》，将“级”解释为“等级”；另一方面，他对“级数”的认识只具其形，在发现所蕴含的规律后，通过类推，以期各率式的求解能依附于“级数”之形。

在《缀术》卷四中，徐有壬使用了“级数式”这一术语，因在前几卷中讨论的对象是“术”，而卷四中讨论的对象由“术”变为“式”，且他在寻求“立法之原”时，试图给出具有一般性的适用方法。

2.2 运算法则

《缀术》卷一的预备知识中还给出了加、减、乘、除法，齐母通分和化分。其中的乘法是用一常数乘，若所乘常数与分母有公因子，可用约去分母中的公因子来代替作乘法。若分母不同者，先齐其分，即用通分法互乘后再相加。“化分”主要为了解决同率名中分母不统一的问题，如：

依据“齐母通分”，“互乘齐之”，“变其式不变其实”，使得弦求矢式的各率式中的分母成“二、二四、二四六”等依次递增之数，同时与西算中级数表达形式保持一致。

2.3 推导方法

“比例法”是基本方法，“还原术”和“借径术”等都以“比例法”为前提，也是“比例法”的应用拓展。“凡第一行式只一位者用此法”［18］，此时第一率式为算式即单项式。较之“比例法”，“比例商除法”的适用范围更广，可将“比例法”纳入其中。由“正弦求余弦式”，用“比例商除法”得“弦求切式”，记“弦求切式”的各率名为ϕn，正弦为ϕ2，半径为r=ϕ1，所求的正切为tanα，余弦为cosα，有：

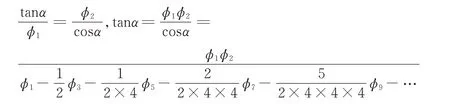
在《象数一原》（1843年）卷二“半分起度弦矢率论”中，项名达所用的“除法式”与戴煦在《外切密率》（1852年）中推导本弧求切线时所用的方法是相同的。从著作的完成时间看，“比例商除法”并非徐有壬首先使用，但他首先给出该方法名称。

“借径术”相当于“代换法”，“还原术”先把“算式”变为“率式”，用“比例法”求各率式，将两率式相乘，通过各率式的加减，最后只剩一新的算式，即为所求。这一过程与明安图的“反求”、李善兰的“回求”等计算思路大体一致。

3 “缀术”运演级数的方法特征

《缀术》卷二伊始，徐有壬表明了欲得“缀术”的前提是求得各率式，各率式“连缀而下”，依据连比例各率，再以各率式为基础，将“式”变为“术”。并指出了“缀术”“能于算术中自成一队者”［18］，是因为在“弦求矢”等问题时，对于出现的开方问题，可通过屡乘屡除的方法来解决。

3.1 矩形的几何解释

前人对徐有壬的几何证明作了细致详尽地推导，本文不再赘述。在这一过程中，徐有壬运用了“出入相补原理”“今有术”“三要法”等初等方法，并结合了“比例商除法”“还原术”“借径术”等推导方法。事实上，并不是徐有壬首先使用此类初等方法解决级数展开问题，早在《割圆密率捷法》卷三的“三法”中，明安图构造了新的几何图形，创造出求二分全弧通弦的方法，在论述中使用了“廉”①指磬折形一侧边之长。、“隅”②指拐角小方形的宽度。和“廉隅共积”③指磬折形面积，即两长方、正方的和。等术语，依次求得初商、次商和三商等，明氏所构造的这一几何模型是用无穷级数来逼近平方根［19］。明、徐作法的不同之处在于前者依据开方术，后者避开开方术。《四元玉鉴》中的类似问题也运用了“出入相补原理”，徐有壬研究了《四元玉鉴》后，对其中的题目及其解题方法都较为熟悉。

3.2 加减差的处理

李俨曾依徐氏原意给出了《测圆密率》中弧背求正切式前六项的系数分子，后来尝试将“一差至四差”等公式化，但结果并不明显。《测圆密率》卷三第13、14、17、18术中均已出现了正切数，但结果不够清晰［7］856。张升［9］111将徐有壬的和式进行了重新组合，对卷三中“差”的系数用公式明确地表示出来，并对“差”作了进一步研究，重新组合得到了形式上的美观，而徐有壬对此略而不述，如此组合仍旧不能摆脱“差”对第几数的依赖。其中的正切级数展开式含有加差形式，是因为徐氏以研究每项之间的递推规律为主要目的，加减差则是辅助函数形式［5］39。

在《缀术》卷四中，他将各率式转化为含有加减差形式的各术，所关注的不再是如何方圆互化，而是如何由“算式”变为“率式”再变为“术”，由“术”再寻求“立法之原”。徐氏将得到的各式分为不含加减差和含有加减差，前一类的各率式系数分子可用递推关系来统一表达，后一类则无法得到统一的表达式。“既得各求式，乃可镕而为术，未能求得差根无可立为术”［18］，表明立术的前提是求得差根，而求得差根则是立术的关键。在“弦求矢式”中，他引入了“分段除法”和“分段乘法”，含有加减差中各式的“分段除法”与“分段乘法”规律较为明显，并且可递推，不含加减差中各式的“分段除法”规律明显，而“分段乘法”规律不明显，需用加减差的形式来解释。为什么徐有壬会引入“缀术”来研究各项之间的关系呢？实际上，要想找到级数展开式的规律就需研究每项的系数规律，徐有壬在明安图和董祐诚等人的工作基础上，观察到各项之间的比例关系，加之有些个别率式中的分子分母有着特殊的比例关系，为此，他想从整体上把握并寻求统一的解决方法，虽在《缀术》中通过大量的计算求出了各加减差，却未能确定求各加减差的递推规律，故未能立术。

3.3 方格捷法的使用

在“比例法”中，徐有壬将方格分为“除、乘、实、得”，满足“乘×实÷除=得”，每个式子相当于单项式与多项式相乘的运算。“若大小八线相求，则中两行相乘须画方格如天元术乘法逐层求之”，因为在大小八线相求中，某些率式中的“率数”不是常数，而是多项式，所以要用天元术［4］666。可见，在简单的“比例法”中“乘”和“实”两列的计算量较小，操作简单，基本为单项式与多项式相乘，但在大小八线相求的“乘”和“实”两列中，运算对象变成了多项式，需要进行多项式与多项式相乘，计算量较大，涉及的步骤较多，因此，方格法可以根据实际的运算对象和计算量的多少来选择。

吴敬将“格子算法”称为“写算”，程大位称为“铺地锦”［20］。写算在后来影响很大，清代数学著作涉及写算的很多［21］。在《缀术》中称为“方格捷法”，使人们对“铺地锦”有了新的认识。“方格捷法”的重要作用在于，一是在方格内可进行齐母通分再相加减的操作，二是在方格内通过虚线的联结即把相同率名的算式放一起，便于进行同类项的合并。

3.4 尾数的截留

一般而言，尾数的截留包括两个方面：项数的截留（即算至哪一项停止）和奇零小数的处理（即实际应用时对小数的处理）。在《缀术》中，有六处专论尾数截留的问题，多出现在左潜的“案语”中。如在“弦求矢式”中，“用比例法求其三率五率，以下各式列之，至十一率止。十一以下连缀不尽，今每式止求五位，故尾数截去不用也”［18］。求五位是指只求三率、五率、七率、九率和十一率。若半径取1，则从首项开始得数即为小数。在实际运算中，当取偶数各率时到ϕ10，取奇数各率时，到ϕ11止［4］674。左潜在《缀术释明》中指出：“求至十一率止，以下截去不用，缘级数式不必多求也”［22］，把原来的“各率式”视为“级数式”，他们已认识到级数展开式的项数是“无穷无尽”的。早在《测圆密率》的每术之后，徐有壬就有“如是递求，至单位下而止”的表述，这一点和明安图的表述相同，即求至出现小数时停止计算。

可见，徐有壬在一开始就指出各率式是“连缀不尽”的，并在计算之前就规定了求至十率或十一率，不关注各率式中数值的变化，也不关注求至十率或十一率后造成的误差问题。但是，徐有壬对“连缀不尽”和“级数式”等的表述，说明了他对级数“无穷无尽”的更深层次的认识。戴煦对这一问题则给出更为详细地分析和说明。

3.5 连缀而下与斜缀而下

在《缀术》卷二中，“求式者连缀而下，连比例各率之式”，即是利用连比例关系求出各率式之系数，从而将“式”变为“术”。从卷四“大小八线相求各式”起，排列方式也发生了变化，由“竖列之”调整为“横列之”，“因各算式太繁，故改用横列”［18］，原竖列的各算式中率数为单层即单项式，当率数变为多层即多项式的时候，竖列的方式不便于表达。对于“横列”后如何表达，徐有壬亦有详细介绍：“其率上旁书者为累除法，率下算式为乘数，与前各式例同，其乘数有数层者，非累乘法数，乃天元式也。”［18］虽调整排列方式前后各式大体相同，均有三部分构成，对于构成要素来讲，却有很大变化。竖列时的各算式由率名、率数和寄母构成，横列后的各算式由率名、累乘法和累除法构成，率名的奇偶不同所表达的意义也不同。“累除法”即系数的分母，“累乘法”的表达较为复杂，若为单层（即单项式）时与竖列的情形相同，若为多层（即多项式）时需用天元术的表达方式。

徐有壬为何提出“斜缀而下”？一是在方格中进行各算式或各率式的加减和率式的自乘（即“铺地锦”方法）；二是计算含有加减差的各率式时，计算量较大，通过“斜缀而下”可验证或直接给出该率式中后续几项。可见，“斜缀而下”是由方格的形式或竖列形式所带来的结果，如果换为横列的形式，以天元式表示，这一效果并不明显，但徐有壬并非发现某种对应后就以“斜缀而下”作为立术的依据，而仅是将“斜缀而下”作为验证的方法。一般情况下，“连缀而下”指同一率式，“斜缀而下”指不同率式，因含有加减差，前者只关注率名的变化而不关注其它变化，后者不仅关注率名而且关注各算式中分母的变化规律。但需要注意的是，“连缀而下”和“斜缀而下”均包含了徐有壬对级数展开中“无穷无尽”的把握，并非完全直观层面上的认识。

4 因式立术，由术立法

“是故‘缀术’之生，因于明氏而又足以尽明氏之变，明氏之未能立式也。试取明氏书驭之以‘缀术’，其递降各率，顷刻可求”［23］，显然，左潜把徐氏“缀术”视为一种推求方法。以往对《缀术》的研究中，更多的是将“缀术”视为一种表达相关运算操作的方法。

从形式上来看，徐有壬接触并深入研读了《四元玉鉴》后，使用了其中的术语和表述方式，指出了“借根方”在表达大小八线相求等问题上的局限性，即分母为多项式时无法有效表达。同时，西学作为“他者”，徐有壬等人不仅对西学作出了回应，而且重新审视了中算。中算家的级数表达式至徐有壬才开始趋于符号化［24］32，“缀术”的影响比微积分方法的影响更深远。如，左潜于《代微积拾级》《代数术》等书出版以后孜孜不倦地发挥徐氏“缀术”，又如，一些中算家在比较了“缀术”和“微积分”之后，明知微积分有许多优越性，却试图把微积分和“缀术”放在同样的位置上，究其心理正在于“缀术”为“国粹”［25］。

从方法上来看，《缀术》中徐有壬将“式”（算式）化为“术”，试图确定展开式中的每一项均以其前若干项的多项式形式表达的递推规律［6］87，再由此递推求得展开式任意项的表达式。“缀术”是《缀术》中“比例商除法”“还原术”和“借径术”的总括［26］，把几种运算手段有机地结合起来，建立一种演绎体系［26］64。“缀术”虽只是其表现形式，究本质而言，当为无穷级数递推研究［24］。至于“缀术”的计算，是通过对原算题的变式从原算法基础上推衍出新的算法，前提则是根据各率式结构的不同，即是否含有加减差先求得各率式，于是各率式的分母有法可寻，而其分子无法可依。

“因式立术”是建立在“算式”的基础上，用“缀术”处理级数问题的一个关键环节，“术”是在“式”的基础上提炼而出的［6］92。其中的算式实指单项式，各率式实指多项式或无穷级数，“术”为一般的无穷级数。整数的一些性质确实能够“移植”到多项式上来［27］，反过来，整式到整数也可以进行形式转换。徐氏之本意是由单一的形式完全统一起来，从而形成一个相互依赖的比较严密的新体系，从整体上研究进而寻求统一的作法。

5 结语

如上所述，徐有壬创造“缀术”与他刚开始接触四元术有关，“缀术”即为天元术的变形，其最终目的是以“缀术”来实现“因式立术，由术立法”，其中的算式指单项式，率式指多项式或无穷级数，“缀术”则是将“级数式”作为一个整体入算，借助四种计算方法推求级数展开式。“缀术”除了作为一种级数表示法之外，更是一种运算方法，“连缀而下”即递推，“缀”是形，“术”是质，“缀术”的质是由“缀术”的形——连缀之形来反映，而“缀术”的形须由“缀术”的质才能显现。概言之，其本质是以算式和率式为基础的连缀而成的运算方法。“因式立术，由术立法”则表明了徐有壬在探求内在原理时，欲将单项式与多项式推广至无穷多项，从而使算式与各率式满足级数式的相关条件。