无穷级数的柯西和与切萨罗和
赵小玲 上海电机学院 文理学院
无穷级数求和问题是级数教学中的一个起点,也是重点和难点。在《高等数学》中,首先定义了无穷级数的收敛和发散,接着才定义了收敛级数的和,这种和称为柯西和。可以发现,此种定义框架下,发散级数是不能求和的。但是,当我们改变和的定义方式时,某些发散级数也能求和,且与柯西和是相容的。意大利数学家切萨罗就提出了另一种定义方式方式,让我们可以求出某些发散的无穷级数的和。
一、柯西和
利用上述定义,即求部分和数列的敛散性,我们可以得到级数的敛散性,并求出收敛级数的和。
例1:用柯西和定义讨论下列级数的和。
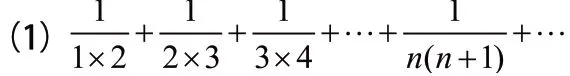
(2)1-1+1-1+…+(-1)n-1+…
(3)1+2+3+4+…+n+…
解:(1) 因为级数的前n 项的部分和
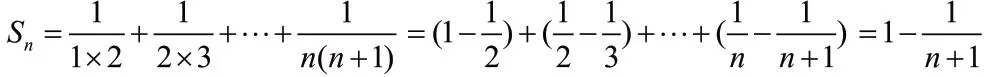
在判断级数收敛或发散时,我们还特别强调了如下一些性质。
(1)收敛级数的逐项和构成的新级数仍然收敛;发散级数的逐项和构成的新级数不一定发散;如果两级数逐项和的新级数发散,原级数中至少有一个发散;如果两级数逐项和的新级数收敛,原级数不一定都收敛。
(2)在级数中增加或减少有限项不改变级数的敛散性;但在收敛时,级数的和数不同的;
(3)在收敛级数上任意加括号构成的级数仍然收敛,且和不变;若加括号构成的级数发散,则原级数一定发散;若加括号构成的级数收敛,原级数不一定收敛(即不能用加括号改变级数运算顺序的方法求级数的和)。 在第三个性质中,着重强调了发散级数求和不能任意加括号。例如是发散的,但是在给此级数用不同的方法加括号以后有:这两个加括号后改变运算顺序的级数均是收敛的,但收敛到不同的数值。表明用任意加括号的方法求级数的和并不科学。
那么,对于发散级数,有没有一种方法可以更好地描绘级数趋近于哪一个常数呢。比如格兰迪级数,它的和一直在0 和1 之间摆动,我们直观上认为,它应该趋近于二分之一比较合理。事实上,用切萨罗求和,确实可以得到这样的结论。
二、切萨罗和
例如:用切萨罗和定义讨论例1 中各级数的和。
解:(1) 因为级数的前n 项的部分和
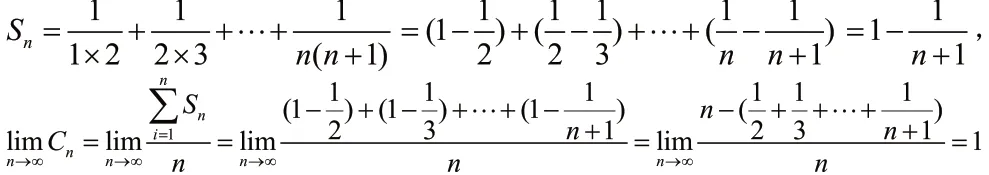
所以级数和为1。可见,此定义方式与柯西和是相容的,即柯西和若存在,则切萨罗和也存在且与柯西和相等。

当然,切萨罗和也不是万能的,对于(3)这个全体自然数相加的发散级数,用切萨罗定义不能求出它的和。
从以上例子可以看出,在研究无穷级数求和的发展过程中有着很多数学理论上的跳跃式发展。全体自然数相加的级数,用切萨罗定义不能求出它的和,但是用拉马努金和的定义方式可以得到一个令人瞠目结舌的 “和”。我们在数学的学习过程中要特别注意数学思维的培养,注意数学架构的严谨清晰,有理有据。在一定的公理体系下,通过严密的逻辑推理,可以发展出不同的数学新分支,丰富数学理论。

