无穷级数敛散性的判别方法探讨

顾 荣

江苏财经职业技术学院 江苏淮安 223003

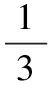
是不是无穷多项的和一定存在呢？我们再来看一个例子：

1+2+4+8+……

基本的数学知识告诉我们，正数相加得到的结果肯定仍然是正数。这里我们假设1+2+4+8+……=，等式左侧我们可以变形为：

1+2×(1+2+4+……)=1+2

所以，我们可以得到：=1+2，由此得出=-1，即1+2+4+8+……=-1。显然，这个结果是错误的，原因就在于我们的假设出了问题。有限项的和是一个确定的数，那么无穷多项的和也一定是确定的数吗？有限项和的运算方法对无穷多项还适用吗？从有限到无限仅仅是简单的数的累加吗？这些其实就是无穷级数的敛散性问题。

一、无穷级数敛散性的判别法及其局限性

(一)利用部分和数列的极限情况判别

在前面“一尺之锤”的例子中，要计算一直取下去，所取得的木棒长度，我们可以先计算取了天后，所得的木棒长度，则:

显然以，，……为项，构成了一个数列{}，该数列称之为部分和数列。

当→∞时，有→1，这也就意味着当木棒一直取下去，所取得的木棒总长度无限接近于1。即：

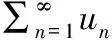
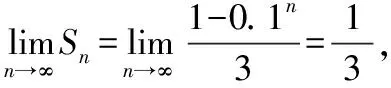
在运用基本判别法讨论无穷级数敛散性时，要求出前项和，我们经常会用到一种方法“拆项相消”。

但是这种方法只适用于部分和是容易求的，或者一般项是容易拆项的，且求和后可以“相消”的级数，但是对于一般项较为复杂的级数，该方法就难以判别敛散性。

(二)利用级数的性质进行判别

还有一些特殊级数我们可以通过将原级数加括号，如果加括号后的级数发散，则可以得到原级数也发散。

例如：

将级数两项两项加括号后，可得：

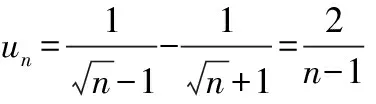
由调和级数敛散性，可得加括号后的级数发散，因此原级数也发散。但是如果加括号后的级数收敛，则无法得到原级数一定收敛。因此，对于一些简单的级数，我们可以利用性质快速判别敛散性。

(三)利用级数收敛的必要条件判别

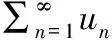
由级数收敛的必要条件告诉我们，判别级数的敛散性，首先要分析该级数的一般项的极限是否为0，如果一般项的极限不为0，则直接可以得到级数发散。

(四)利用比较、比值、根植审敛法判别

比较、比值、根植判别法使用时首先需要清楚的是，它们只适用于正项级数的敛散性判别，因此在判别级数敛散性之前要先辨析该级数是不是正项级数。

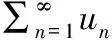
比值、根植判别法在使用时，一般用于中出现了、、!等情况，但是当极限值为1的时候，这两种方法失效。

(五)利用莱布尼兹审敛法判别

莱布尼兹审敛法只适用于交错级数的判别，并且只能判别收敛的交错级数。该审敛法在使用时需要讨论一般项的单调性，所以有时需要通过函数的单调性来讨论。

(六)利用绝对收敛来判别

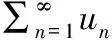
二、无穷级数敛散性的判别流程及举例

级数敛散性的判别方法有很多，但是有些判别方法又具有一定的局限性，只能判别某一类级数的敛散性。这就导致很多学生在面对具体级数敛散性的讨论时，徒有很多方法，却往往不知所措。因此，在掌握了各种判别方法的基础上，要能够灵活运用各种判别方法，取长补短，准确地分析具体问题的解决方法，就需要理清楚级数敛散性判别的流程。

敛散性判别流程图

首先看级数的一般项的极限是否为0，如果不为0，则可以直接判定该级数发散；若极限等于0，则需观察级数是否为正项级数；若是，则利用比值或根植判别法判别，当比值、根植判别法失效时需要使用比较判别法或者利用部分和数列极限情况来讨论敛散性。如果不是正项级数，则需根据项的排列规律分析级数是否为交错级数。若是，则使用莱布尼兹判别法判断级数是否满足条件，如果满足条件，则级数收敛，否则，需要判断绝对收敛性，即转化为正项级数讨论。如果级数既不是正项级数也不是交错级数，则也需要通过绝对收敛性判断。

下面通过几个例子说明如何根据上图中的流程来判别级数的敛散性。

分析：该级数中含有参数，且一般项中含有，所以需要对参数范围进行分类讨论：

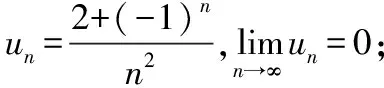
由以上几个例子可以看出，对于某一无穷级数敛散性的讨论，可能需要用到多种判别方法，这就需要我们能够灵活地掌握判别方法以及基本流程。但是无论如何，题目都是“万变不离其宗”，复杂的题目可以让我们在解题过程中多一份感受，也更深刻地认识它的本质。