不相交线性码的一种新构造*
董雪雯, 孙玉娟
1.西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 西安710071
2.密码科学技术国家重点实验室, 北京100878
1 引言
密码函数包括单输出布尔函数和多输出布尔函数, 是构成密码算法的重要部件, 主要用于流密码和分组密码的设计.在流密码和分组密码体制中, 为了抵抗多年来相继出现的各种攻击方式, 一个密码函数需要满足以下指标: 高非线性度、平衡性、相关免疫性、高代数次数、最优代数免疫度和良好自相关性质等等.然而密码函数的各项指标之间存在相互制约, 如何实现这些指标的折中优化是密码函数设计中的重要难题.
Berlekamp-Massey 攻击、相关攻击是攻击流密码的重要方法, 抵抗Berlekamp-Massey 攻击需要高非线性度, 抵抗相关攻击需要高阶相关免疫, 而高非线性度与高阶相关免疫相互制约, 平衡的相关免疫函数通常称为弹性函数, 因此非线性度高的弹性密码函数的设计是一个重要的研究课题.[n,k]线性码是n维向量空间的k 维线性子空间, 在高非线性度弹性密码函数的构造中起着重要作用[1–8].
2003年, Johansson 和Pasalic[2]首次利用不相交[n,k]线性码构造具有高非线性度的多输出弹性密码函数.为了得到不相交[n,k]线性码, 他们采用的方法是计算机搜索.这种方法只在n 和k 都比较小时才是可行的.2004年, Niederreiter 和Xing[9]给出了基于代数函数域上的不相交线性码的构造, 这种方法能找到的不相交线性码数量很少.2005年, Charpin 和Pasalic[3]利用射影空间的基本理论构造了不相交线性码, 利用这种不相交[n,k]线性码也可以构造具有高非线性度的多输出弹性密码函数, 这种构造不相交线性码的方法只有在k 整除n 时才可行.2014年, 张卫国和Pasalic[1]利用不相交线性码构造了能达到严格几乎最优非线性度的弹性S 盒, 另外还利用不相交线性码构造了PS 类bent 函数和完全非线性S 盒.该篇论文充分利用了不相交线性码, 这提示我们不相交线性码在密码函数的构造中有重要价值.其中还给出了一种不相交线性码的构造方法.这种方法生成的不相交[n,k]线性码的个数为其中当k |n 时, N(n,k)达到了最优值; 当kn 时, 所得不相交[n,k]线性码的个数是目前已知最好的结果.在kn 时, 是否存在一种方法能生成更多的不相交[n,k]线性码, 是值得进一步研究的问题.由于张卫国和Pasalic[1]在构造不相交[n,k]线性码时, 需要借助很多个不同次数的本原多项式来进行计算, 其个数与成正比.因此, 当n ≫k 时, 计算量很大.本文提出了不相交[n,k]线性码的一种新构造, 即使当n、k 很大或n ≫k 时, 仍可以快速有效地得到大量不相交[n,k]线性码.
在本文构造中, 当k | n 时, 只需要借助一个k 次本原多项式便可生成个不相交[n,k]线性码, 其中也就是说此时生成不相交[n,k]线性码的个数达到了最优.当kn时, 只需要借助一个k 次本原多项式和一个m 次本原多项式便可生成大量的不相交[n,k]线性码, 其中此时生成不相交[n,k]线性码的的个数与文献[1]生成不相交[n,k]线性码的个数相同.本文的构造在保证生成不相交[n,k]线性码的个数与文献[1]生成不相交[n,k]线性码的个数相同的情况下, 很大程度上简化了计算过程, 极大地减少了计算量.越大, 本文构造的优势越明显.后文的结构如下: 第2 节, 主要介绍了线性码和不相交线性码的相关基础知识; 第3 节, 描述了一种构造不相交线性码的新方法, 并给出相关证明; 第4 节, 对本文工作进行了总结.
2 基础知识
定义1将GF(2)上的n 维向量空间记为Vn, Vn的k 维线性子空间Vk称为[n,k]线性码, 记为C(n,k).[n,k]线性码共有2k个n 维向量.
定义2以[n,k]线性码C 的基底向量构成的矩阵称为该[n,k]线性码的生成矩阵, 记为G(n,k).
定义3设{C0(n,k), C1(n,k), ··· , Ct(n,k)} 均为[n,k]线性码, 如果Ci(n,k)∩Cj(n,k)={01×n}, 其中0i,jt, 且ij, 则称Ci(n,k), Cj(n,k)互为不相交[n,k]线性码.
引理1将不相交[n,k]线性码的个数记为N(n,k), 则
引理2令k,m,v 均为正整数,其中km,v =2m−1.α 是F2m 上的本原元,(1,α,α2,··· ,αm−1)是F2m/F2上的基.定义同构σ :F2m →为
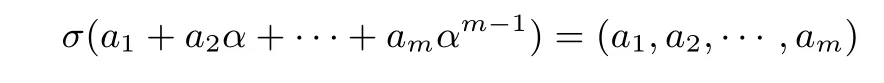
其中F2m上的零元素映射成中的零向量.令
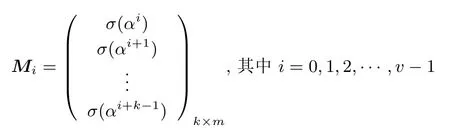
则矩阵(Ik,Mi)是一系列不相交[k +m,k]线性码Ci(k +m,k)对应的生成矩阵Gi(k +m,k), 其中i = 0,1,2,··· ,v −1.当矩阵(Ik,Mi)是一系列不相交[k+m,k]线性码对应的生成矩阵时, 矩阵(A,Ik,B,Mi,C)也是一系列不相交线性码对应的生成矩阵, 其中A, B, C 为任意k×j 的矩阵, j 为任意非负整数.
证明:Ci1(k + m,k)的每个码字是Gi1(k + m,k)的线性组合, Ci2(k + m,k)的每个码字是Gi2(k+m,k)的线性组合.要证Ci1(k+m,k)与Ci2(k+m,k)互为不相交线性码,则只要证Gi1(k+m,k)中任意一行都与Gi2(k+m,k)线性无关即可, 其中i1i2.很显然, 当i1i2时, (Ik,Mi1)中任意一行都与(Ik,Mi2)线性无关.因此, 矩阵(Ik,Mi)是一系列不相交[k+m,k]线性码对应的生成矩阵.
3 构造方案
构造1令n, k, m, v1, v2, u 均为正整数, 且kn, n>2k, m=n −uk, v1=2k−1, v2=2m−1,将k×k 的单位矩阵记为Ik, 将k×k 的零矩阵记为0k, 将k×m 的零矩阵记为0′.α 是F2k上的本原元,是F2k/F2上的基, β 是F2m 上的本原元,是F2m/F2上的基.分别定义同构π1:F2k→π2:F2m →为
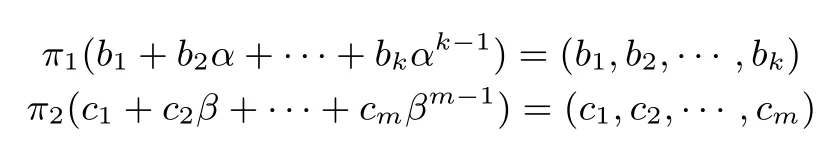
其中F2k上的零元素映射成中的零向量, F2m 上的零元素映射成中的零向量.令

其中i=0,1,2,··· ,v1−1, j =0,1,2,··· ,v2−1.令As是一个k×k 的矩阵, 其中s=1,2,··· ,u;A′是一个k×m 的矩阵.[n,k]线性码对应的生成矩阵G(n,k)是一个k×n 的矩阵, 表示为
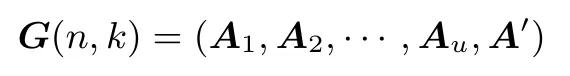
我们分三大步构造这种不相交线性码的生成矩阵,
• 第一步: 令A1=0k, (A2,··· ,Au,A′)=G(n −k,k).其中, G(n −k,k)为不相交[n −k,k]线性码.称其为第I 类[n,k]线性码, 共有w 个, 其中w 为不相交[n −k,k]线性码的个数.
• 第二步: 令A1=Ik, A′=0′.而后将第二步分成u 小步完成, 称其为第II 类[n,k]线性码.
– 第2 步, 对于某一s1∈{2,3,··· ,u}, 令As1=Mi.对于任意ss1, 令As=0k.i 从0 遍
历到v1−1.称其为第II-2 类[n,k]线性码, 共有个;
...
– 第r+1 步, 对于s1,s2,··· ,sr∈{2,3,··· ,u}, 令Ast= Mit, t =1,2,··· ,r, 当t1t2时,st1st2.对于任意sst, 令As= 0k, t = 1,2,··· ,r.对于任意it都从0 遍历到v1−1.
其中r =0,1,2,··· ,u −1.
...
– 第u 步, 对于st=2,3,··· ,u, 令Ast=Mit, t=1,2,··· ,u −1, 当t1t2时, st1st2.同样, 对于任意it都从0 遍历到v1−1.称其为第II-u 类[n,k]线性码, 共有个.
• 第三步: 令A1= Ik, A′=而后将第三步分成u 小步完成, 称其为第III 类[n,k]线性码.这u 小步与第二大步里的u 小步相同, 分别称其为第III-(r +1)类[n,k]线性码, 其中r =0,1,2,··· ,u −1.因为与0′的差别, 其中j 从0 遍历到v2−1, 所以第三步生成的不相交线性码共有
证明:因为G(n −k,k)是一系列不相交[n −k,k]线性码的生成矩阵, 所以第I 类[n,k]线性码是不相交线性码.由引理2 可知, 第II-(r+1)类[n,k]线性码是不相交线性码, 其中r =1,2,··· ,u −1.同理, 第III-(r+1)类[n,k]线性码是不相交线性码, 其中r = 1,2,··· ,u −1.对于第二大步, 因为每一小步中, 值为Mi的As的个数都不同.所以对于任意第II-r1类不相交线性码和任意第II-r2类不相交线性码, 总存在第II-r1类不相交线性码中Ast1= Mi, 而第II-r2类不相交线性码中Ast1= 0k, 其中r1r2.因此第II 类[n,k]线性码是不相交线性码.同理, 第III 类[n,k]线性码是不相交线性码.因为在第I 类[n,k]线性码中A1=0k, 而在第II 类[n,k]线性码和第III 类[n,k]线性码中A1=Ik, 所以第I 类与第II 类不相交, 第I 类与第III 类也不相交.在第II 类[n,k]线性码中A′= 0′, 在第III 类[n,k]线性码中A′=所以第II 类与第III 类不相交.因此, 用这种构造方法得到的[n,k]线性码是不相交线性码.
因为G(n −k,k)也是由Ik, 0k, 0′, Mi,构成的.所以在整个构造过程中, 我们只需要Ik, 0k,0′, Mi,五种矩阵.其中借助一个k 次本原多项式和一个m 次本原多项式即可得到所有的Mi和在很大程度上简化了计算过程, 减少了计算量.
定理1将构造1 生成[n,k]不相交线性码的数量记为N1(n,k).N1(n,k)=1+n>k,且
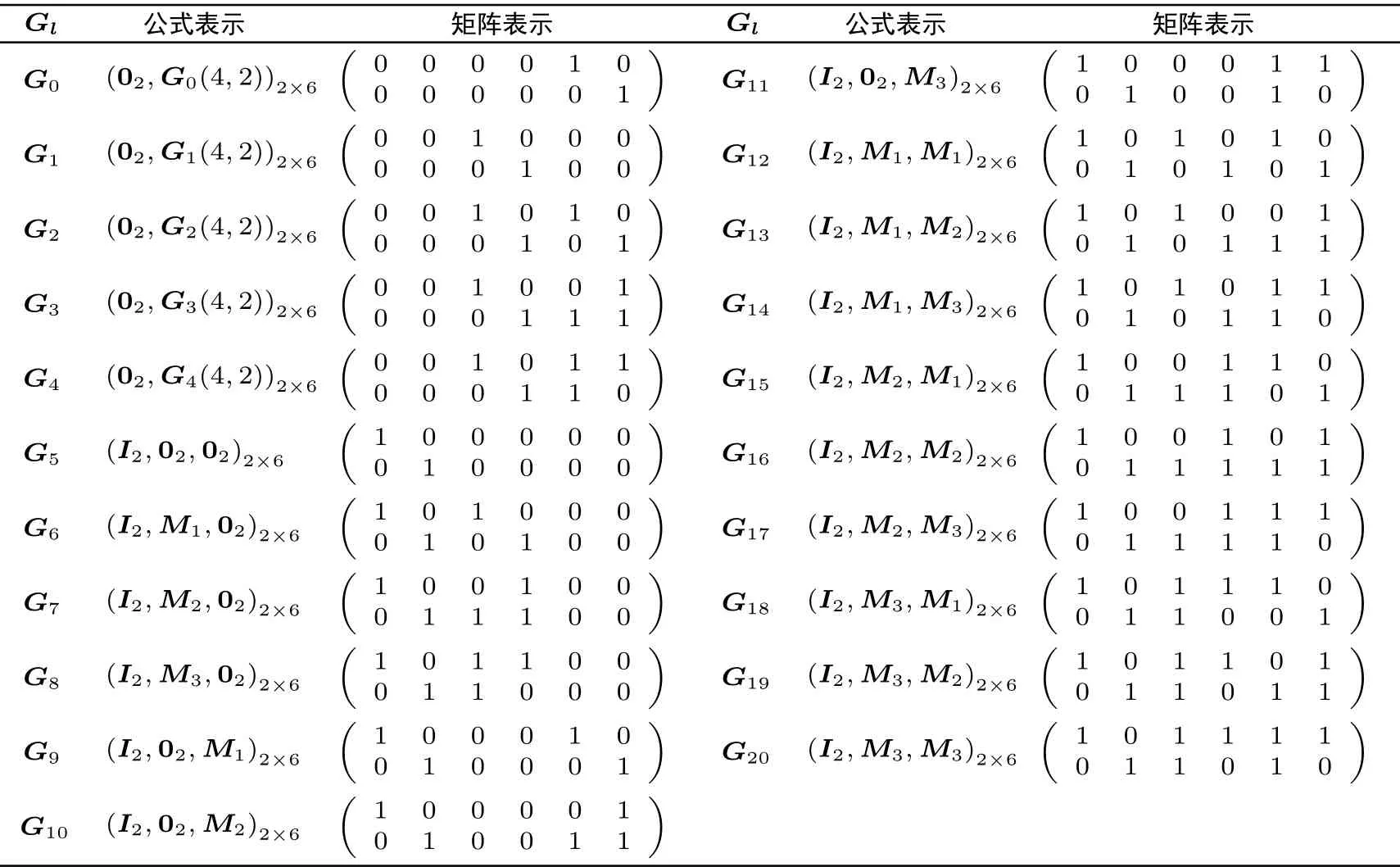
证明:当n=2k+b, 0 其中Gl(k+b,k)=(Ik,0k×b), 则N1(2k+b,k)=1+2m, 此时符合定理. 假设当n=ak+b 时, 满足N1(n,k)=1+ 当n=(a+1)k+b 时, 即此时符合定理. 综上, 得证. 例1由构造1 生成不相交[10,3]线性码, 此时n = 10, k = 3, m = 4, v1= 7, v2= 15, u = 2,N1(n,k)= 145, w = 17, δ = 1.π1(α0)= (1,0,0), π1(α1)= (0,1,0), π1(α2)= (0,0,1), 可取本原多项式, p(x)= x3+x+1, 此时, π1(α3)= (1,1,0), π1(α4)= (0,1,1), π1(α5)= (1,1,1), π1(α6)= (1,0,1).π2(β0)= (1,0,0,0), π2(β1)= (0,1,0,0), π2(β2)= (0,0,1,0), π2(β3)= (0,0,0,1), 可取本原多项式p(x)= x4+ x + 1, 此时, π2(β4)= (1,1,0,0), π2(β5)= (0,1,1,0), π2(β6)= (0,0,1,1), π2(β7)=(1,1,0,1)等等, 这里不再一一列出.简略地列出所生成的不相交[10,3]线性码对应的生成矩阵Gl(10,3)为 例2由构造1 生成不相交[11,3]线性码, 此时n = 11, k = 3, m = 5, v1= 7, v2= 31, u = 2,N1(n,k)= 289, w = 33, δ = 3.π1(α0), π1(α1), ···, π1(α6)同例1.π2(β0)= (1,0,0,0,0), π2(β1)=(0,1,0,0,0), π2(β2)= (0,0,1,0,0), π2(β3)= (0,0,0,1,0), π2(β4)= (0,0,0,0,1), 可取本原多项式p(x)=x5+x2+1.简略地列出所生成的不相交[11,3]线性码对应的生成矩阵Gl(11,3)为 例3由构造1 生成不相交[13,3]线性码, 此时n = 13, k = 3, m = 4, v1= 7, v2= 15, u = 3,N1(n,k)= 1169, w = 145, δ = 1.π1(α0), π1(α1), ···, π1(α6)同例1.π2(β0), π2(β1), ···, π2(β14)同例1.简略地列出所生成的不相交[13,3]线性码对应的生成矩阵Gl(13,3)为 构造2k |n 是kn 的特殊情况, 即即在整个构造过程中, 我们只需要Ik, 0k, Mi三种矩阵, 只需要借助一个k 次本原多项式即可得到所有的Mi.这在更大程度上简化了计算过程, 减少了计算量.此时, 还有更简洁的构造过程.令As是一个k×k 的矩阵, 其中s=1,2,··· ,u+1.[n,k]线性码对应的生成矩阵G(n,k)是一个k×n 的矩阵, 表示为 我们分两大步构造这种不相交线性码的生成矩阵, • 第一步: 令A1= 0k, (A2,··· ,Au,Au+1)= G(n −k,k), 其中G(n −k,k)为不相交[n −k,k]线性码.称其为第I 类[n,k]线性码, 共有w 个, 其中w 为不相交[n −k,k]线性码的个数. • 第二步: 令A1=Ik.而后将第二步分成u+1 小步完成, 称其为第II 类[n,k]线性码. – 第2 步, 对于某一s1∈{2,3,··· ,u+1}, 令As1=Mi.对于任意ss1, 令As=0k.i 从0遍历到v1−1.称其为第II-2 类[n,k]线性码, 共有个; ... – 第r+1 步, 对于s1,s2,··· ,sr∈{2,3,··· ,u+1}, 令Ast=Mit, t=1,2,··· ,r, 当t1t2时, st1st2.对于任意sst, 令As=0k, t=1,2,··· ,r.对于任意it都从0 遍历到v1−1.称其为第II-(r+1)类[n,k]线性码, 共有个; 其中r =0,1,2,··· ,u. ... – 第u+1 步, 对于st=2,3,··· ,u+1, 令Ast=Mit, t=1,2,··· ,u, 当t1t2时, st1st2.同样, 对于任意it都从0 遍历到v1−1.称其为第II-(u+1)类[n,k]线性码, 共有个. 证明:同理构造1, 第I 类[n,k]线性码是不相交线性码; 第II-(r+1)类[n,k]线性码是不相交线性码, 其中r =1,2,··· ,u; 第II 类[n,k]线性码是不相交线性码; 第I 类与第II 类不相交.因此, 用这种构造方法得到的[n,k]线性码是不相交线性码. 定理2将构造2 生成[n,k]不相交线性码的数量记为且 证明:当n=2k 时, 按构造2 生成的不相交[n,k]线性码对应的生成矩阵为 其中Gl(k,k)=Ik, 则N2(2k,k)=1+2k, 此时符合定理. 当n=(a+1)k 时, 即此时符合定理. 综上, 得证. 例4用构造2 生成不相交[6,2]线性码, 此时n = 6, k = 2, v = 3, u = 2, N2(n,k)= 21, w = 5,π1(α0)= (1,0), π1(α1)= (0,1), 可取本原多项式p(x)= x2+x+1, 此时, π1(α2)= (1,1).由构造2 生成的不相交[6,2]线性码对应的生成矩阵Gl(6,2)见表1. 表1 不相交[6,2]线性码对应的生成矩阵Table 1 G of disjoint [6,2]linear codes 例5用构造2 生成不相交[9,3]线性码, 此时n = 9, k = 3, v = 7, u = 2, N2(n,k)= 73, w = 9.π1(α0), π1(α1), ···, π1(α6)同例1.简略地列出所生成的不相交[9,3]线性码对应的生成矩阵Gl(9,3)为 例6用构造2 生成不相交[12,3]线性码, 此时n=12, k =3, v =7, u=3, N2(n,k)=585, w =73.π1(α0), π1(α1), ···, π1(α6)同例1.简略地列出所生成的不相交[12,3]线性码对应的生成矩阵Gl(12,3)为 本文给出了不相交[n,k]线性码的新构造.通过该构造生成的不相交线性码的个数为目前已知最优.本文运用简洁明了的划分方式生成了一系列的不相交线性码, 使得在k 整除n 和k 不整除n 两种情况下生成不相交线性码的计算量都比现有构造方法的计算量小.本文构造的不相交线性码可以用于流密码系统中具有高非线性度的多输出弹性密码函数的构造.我们给出了一部分本文构造所生成的不相交线性码的个数, 见表2. 表2 本文构造所生成的不相交[n,k]线性码的个数Table 2 Number of disjoint [n,k]linear codes in proposed works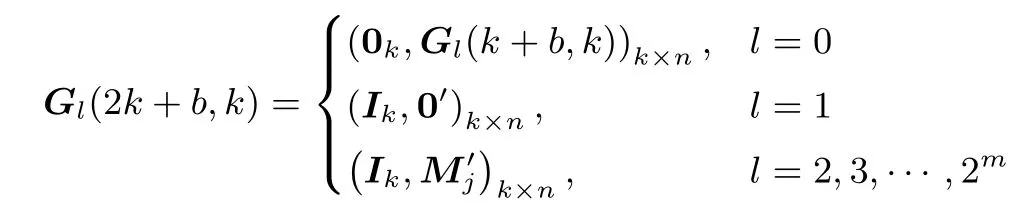

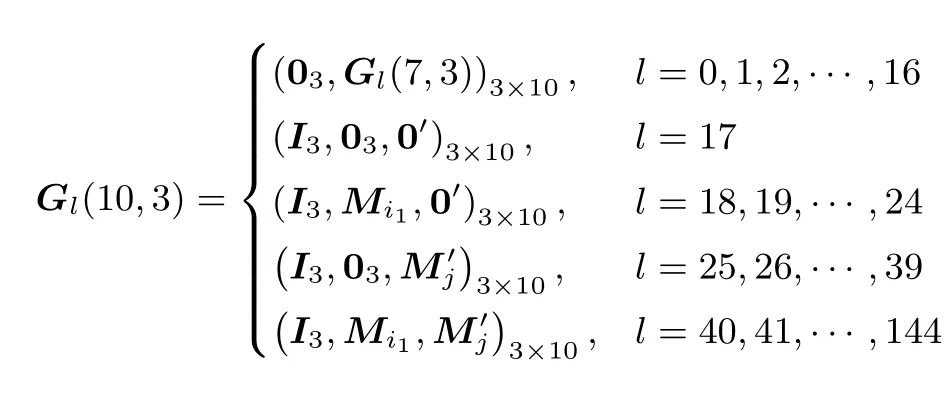
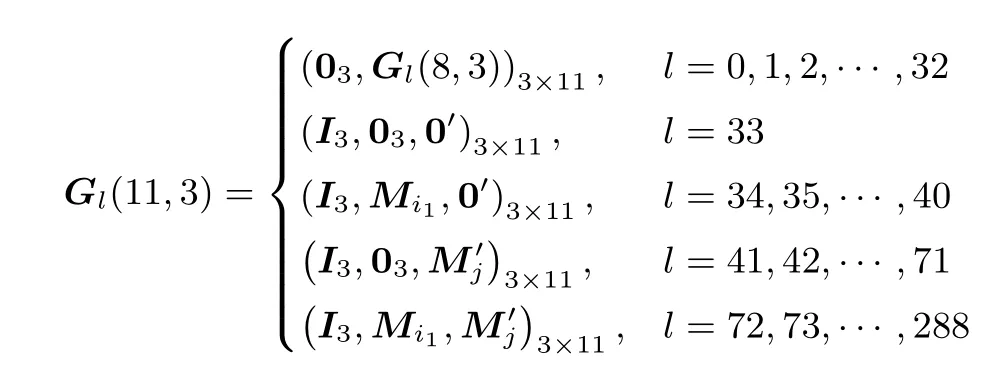
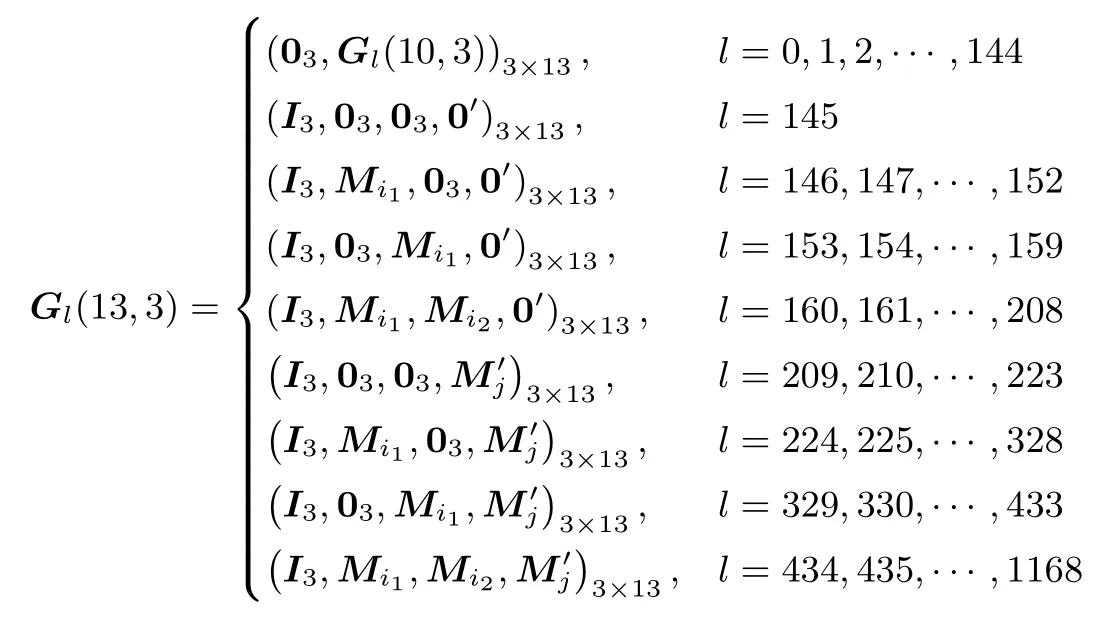
3.2 k |n
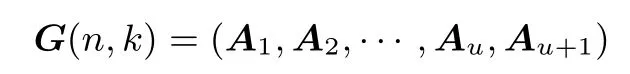
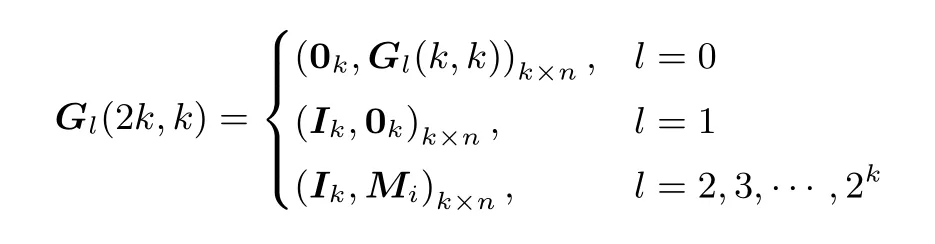
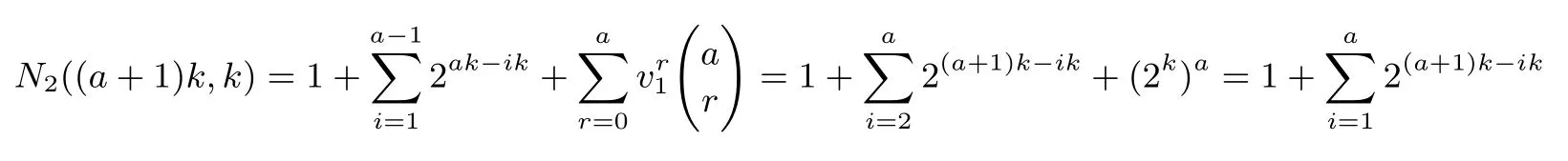
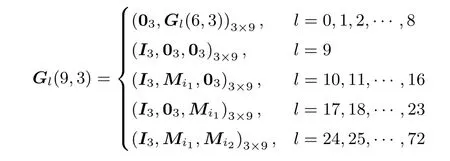
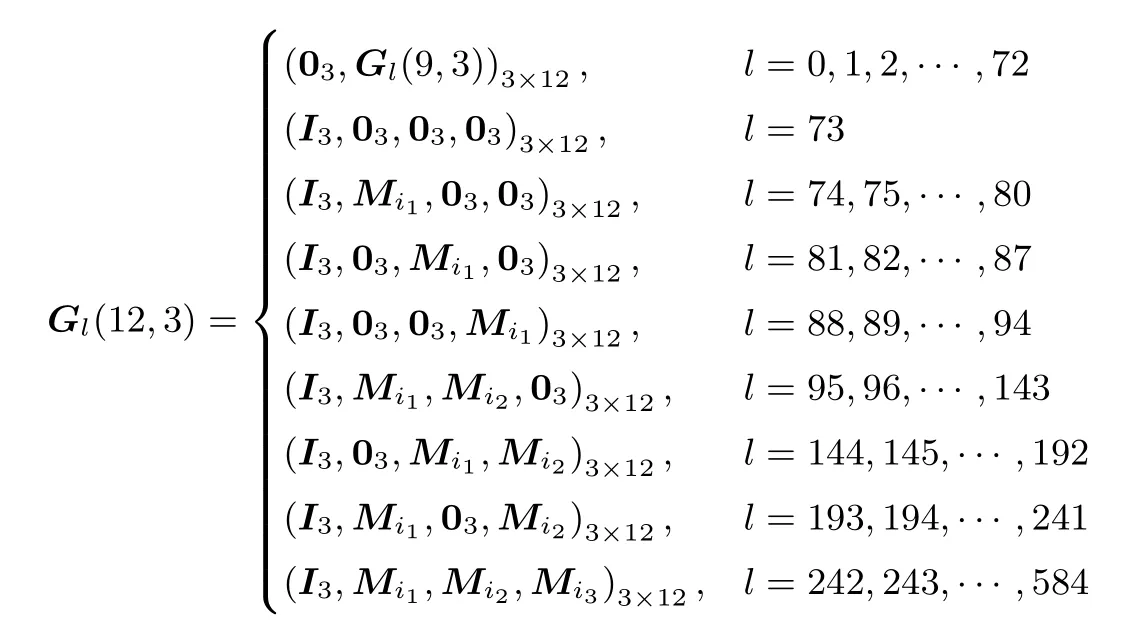
4 总结