基于SSD和ICA降噪的滚动轴承故障诊断*
陈 森,张 浩,甄 冬,师占群
(河北工业大学机械工程学院,天津 300401)
0 引言
滚动轴承在机械传动系统中占据着重要的角色,是机械生产制造的核心零件,然而轴承所处的工作条件极其恶劣,常常面临高温、高压、潮湿和交变载荷的外部环境,极其容易产生故障,所以对轴承的检测和诊断具有重大意义。然而轴承早期故障特征较为微弱,故障信号容易淹没在噪声中,为轴承的诊断、检测增加了较大难度[1-3]。
奇异谱分析(Singular Spectrum Analysis, SSA)又称奇异值分解(Singular Value Decomposition, SVD),是一种非参数化谱估计的先进信号处理方法[4],近些年来由数学领域应用到了旋转机械的故障诊断研究领域,很多专家对其做了相关研究。何志坚等将FSWT与奇异值分解结合,对具有多重故障的轴承振动信号提取出了具有周期特性的冲击成分[5];唐贵基等提出了改进的奇异谱分解结合奇异值分解的方法,并成功应用到齿轮箱的故障诊断中[6]。但SVD在构造轨迹矩阵时无法自适应选取嵌入维数,凭借经验选择会对结果产生较大影响[7]。因此,2014年BONIZZI等在SVD的基础上提出了奇异谱分解(Singular Spectrum Decomposition, SSD)算法[8],SSD克服了SSA的缺陷,可以自适应选取嵌入维数的大小,并从原始时间序列中分解出若干奇异谱分量(Singular Spectrum Component, SSC)。如今,该方法在科学研究领域已经得到广泛应用。
独立成分分析( Independent Component Analysis, ICA) 可以将线性混合时间序列中相互独立的成分分离出来。在旋转机械故障监测、特征提取中已经得到了初步的应用[9]。快速独立分量分析(Fast Independent Component Analysis, FastICA)以负熵最大进行寻优,其计算复杂度较低,稳定性好[10]。为了能分离源信号,通常需要构造虚拟噪声信号,将原始信号与虚拟噪声信号构成新的矩阵,将其作为观测信号采用ICA进行用分离,但工程实践中噪声信号是不可知的,若引入的虚拟噪声不理想将对降噪效果产生较大影响[11]。
本文基于滚动轴承振动信号的特点,提出了基于SSD-ICA联合降噪的滚动轴承故障诊断方法,通过SSD-ICA对原始振动信号进行降噪处理,将ICA分离后的源信号进行Hilbert包络分析,提取故障特征频率。通过仿真分析和实验研究均证明该方法降噪效果理想,提取的故障特征清晰准确,与其他方法相比更高效。
1 理论分析
1.1 奇异谱分解
奇异谱分解(SSD)是一种基于SSA改进新的信号处理方法。通过新形式轨迹矩阵的构建,将原始信号分解为多个频带从高到低顺序排列的奇异谱分量,基本步骤如下:
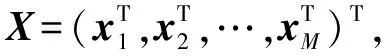
(2)嵌入维数M的自适应选择。通过j次迭代将会产生一个残余分量vj(n),vj(n)的计算表达式如下:
(1)
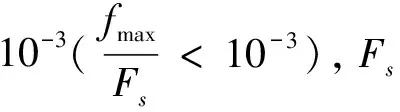
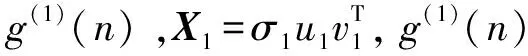
(4)设置迭代终止条件。计算出的SSC逐个从原始信号中除去后余下v(j),根据公式(2)计算残余序列与原始序列归一化均方差,即:
(2)
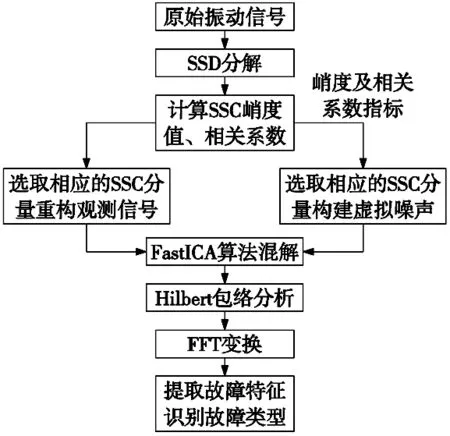
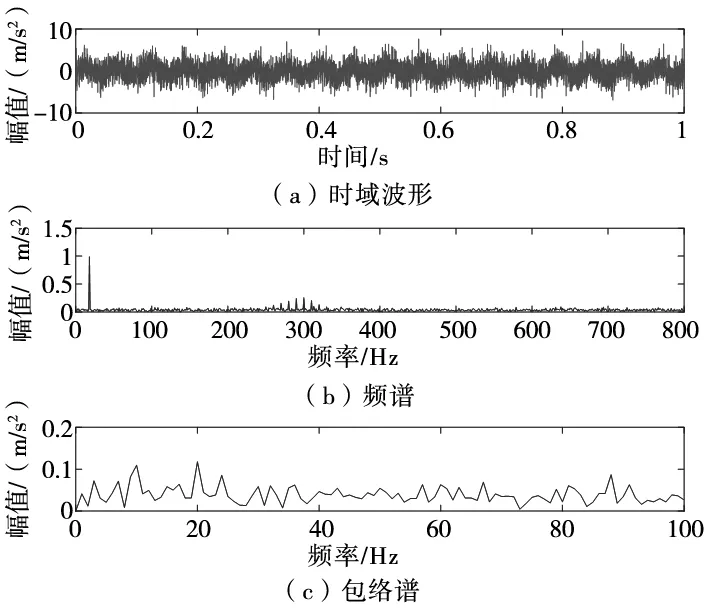
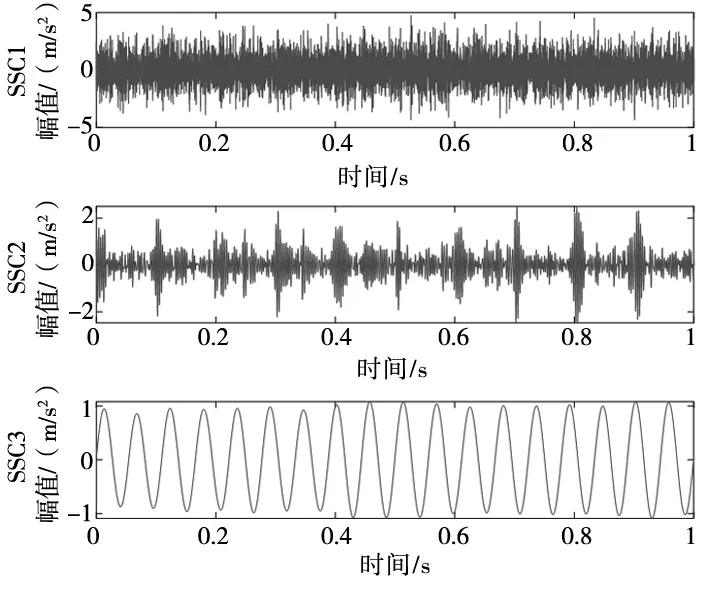
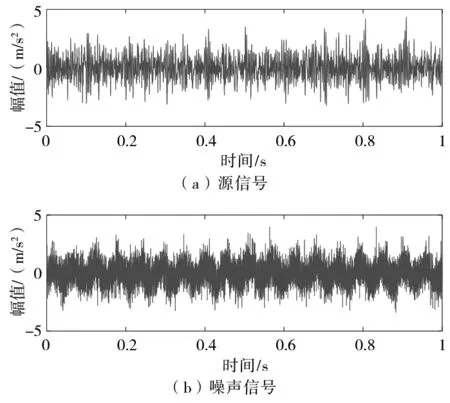
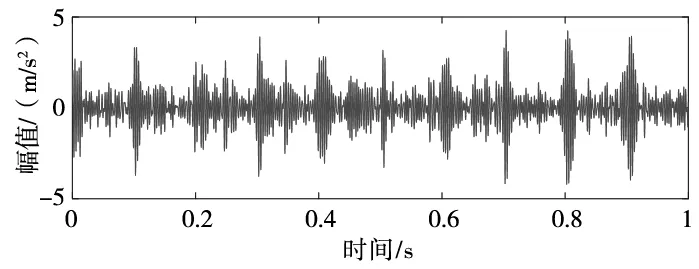
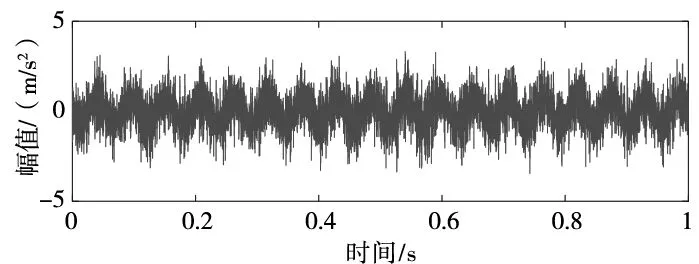
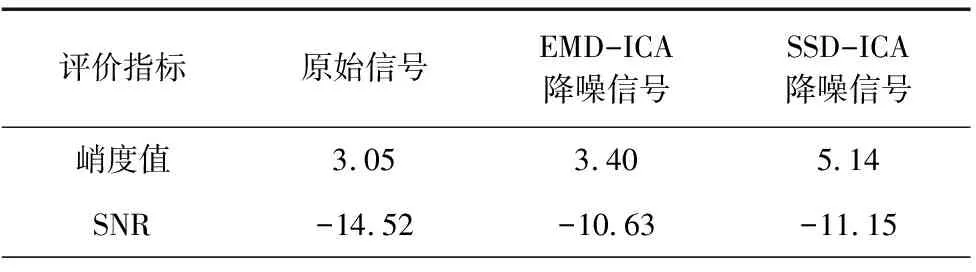
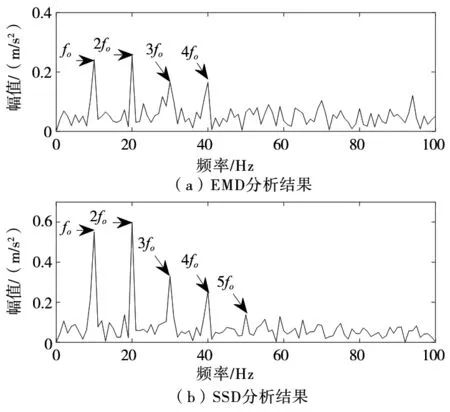
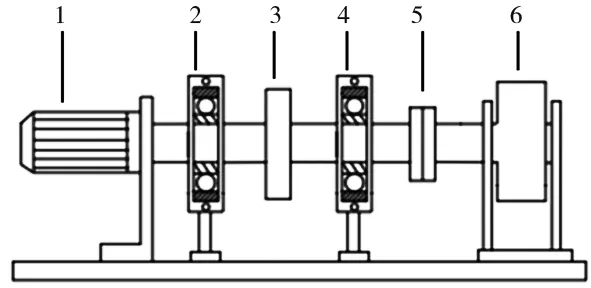
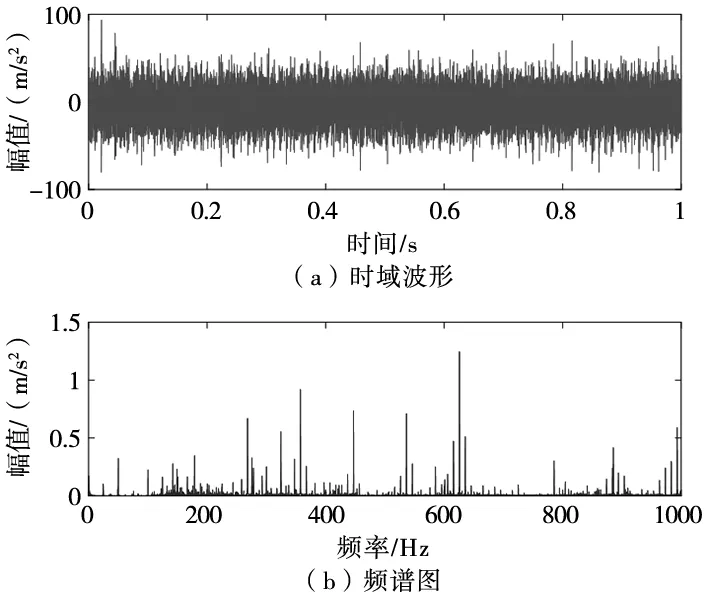
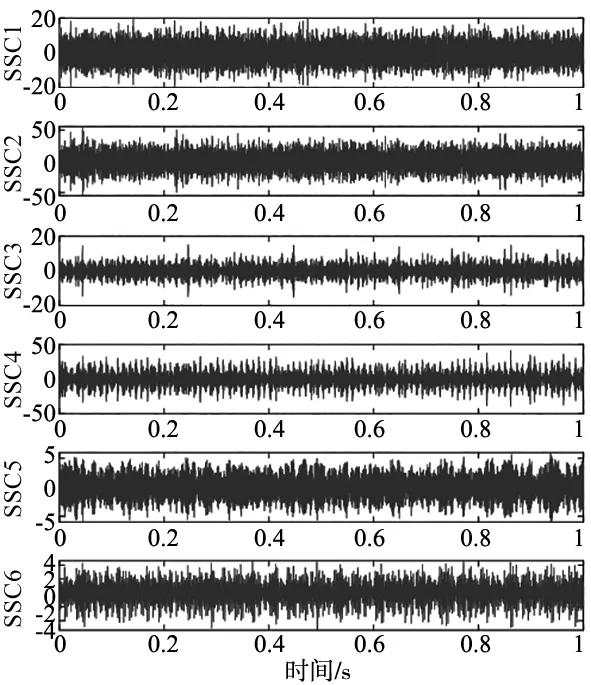
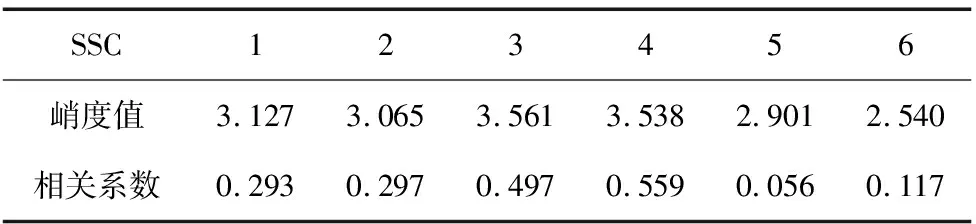
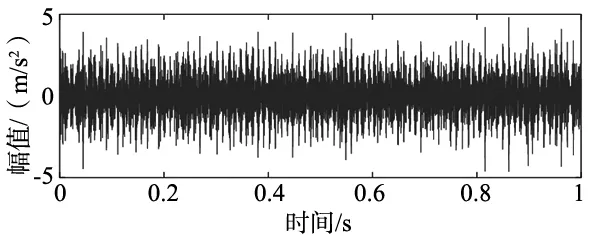
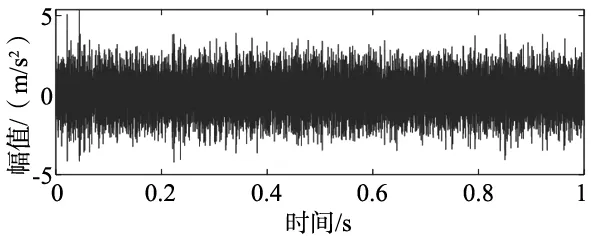
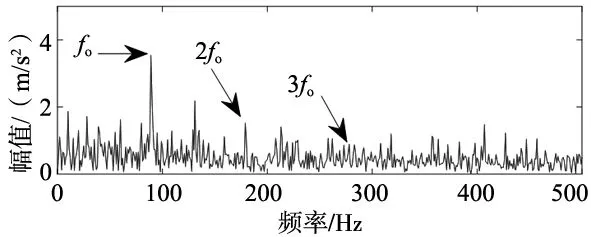
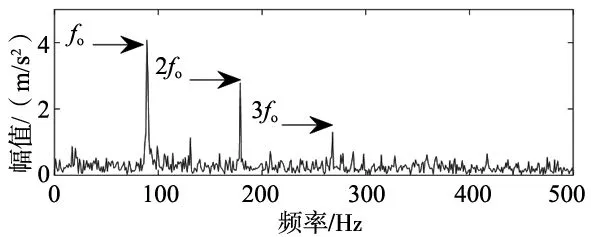
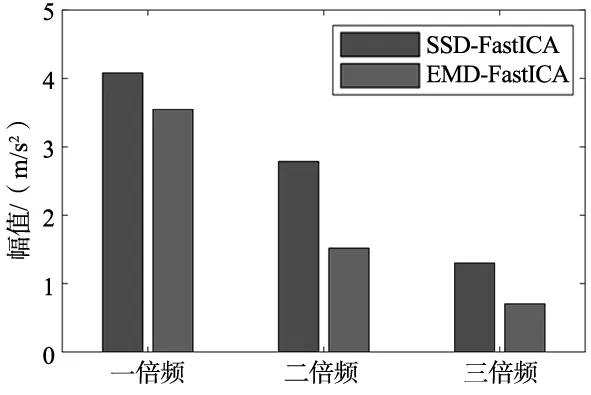
如果计算结果小于预先给定的阈值,分解结束;否则,继续对v(j)分解,直到NMSE (3) 其中,m代表获取的SSC的个数。 在ICA算法中,随机变量负熵定义式可表示为: J(x)=H(xg)-H(x) (4) 式中,xg为高斯随机变量,其与x具有相同的协方差。 由于随机变量概率密度未知,无法采用上述公式直接计算,随机信号的概率密度表达式可通过高阶累计量估计得出,负熵近似表示为: J(x)∞{E[G(x)-E[G(Xg)]]}2 (5) (6) 归一化后得:Wk+1=Wk+1/‖Wk+1‖其中:g(·) 是G(·)的一阶导数,g′(·)是G(·)二阶导数。G(·)表达式为: (7) 通过上述分析可知,ICA算法主要步骤如下: (2)设p=1,m为分离信号的个数。 (3)初始化Wp: Wp=Wp/‖Wp‖ (8) (4)更新Wp,令: (9) (5)正交化Wp (10) (6)归一化Wp: Wp=Wp/‖Wp‖ (11) (7)分析Wp的敛散性,若发散则继续下一步,否则跳转第(4)步。 (8)令p=p+1,若其大于m,独立分量可以被分离出来,否则跳转第(3)步。 螃蟹笑声未止,又见蜈蚣从树上掉下来。螃蟹嘻嘻哈哈地教导蜈蚣,腿多不顶用!为什么呢?你知道吗?蜈蚣摇摇头,说自己不知道,请螃蟹先生指教。螃蟹逐个拍打自己的八条粗腿,自信满满地教导蜈蚣,粗腿有力,攻无不克,战无不胜,天下无敌。 轴承在实际工作中,常伴随着背景噪声,而且信号在传递过程中会由于能量损失造成衰减,受诸多因素影响,轴承的故障特征表现较为微弱,信号经过ICA处理能够将冲击特征凸显出来,但主要是关于多观测通道的研究,本文对原始信号进行SSD处理,依据峭度和相关系数选取SSC分量构造虚拟噪声通道,提出了一种基于SSD-ICA联合降噪方法。算法步骤及流程如图1所示。 图1 SSD-ICA降噪流程 为了表明本文所采取的方法对轴承故障诊断的有效性,构造如下仿真信号: (12) 仿真信号s(t)由3部分组成,其中s1(t)频率为18 Hz正弦信号,作为谐波干扰信号;s2(t)模拟轴承故障信号,其中t1=mod(t,1/f0),其f0=10 Hz为故障特征频率,衰减系数为-80,转频为120 Hz;s3(t)为信噪比为-5 dB的随机信号,用于模拟背景噪声。 仿真信号的采样频率8192 Hz,采样点个数为8192。由图2所示,由于噪声的存在对仿真信号s(t)产生较大影响,图2a时域中冲击成分被淹没,图2b频域中只有谐波干扰信号的频率明显,图2c包络谱也未提取到清晰的故障特征成分,不能判断是否已经产生了故障。 图2 仿真信号时域图、频域图及包络谱图 对s(t)进行SSD-ICA分析,首先将s(t)进行SSD分解,如图3所示,得到3个SSC分量。由图可知,SSC2和SSC3分量较真实的还原了仿真信号中的冲击分量和谐波分量,选取SSC2分量作为原始信号G1(t),将剩余的其他2个分量信号重构为虚拟通道信号G2(t),将G1(t)、G2(t)构成矩阵G(t)=[G1(t);G2(t)]。 图3 仿真信号SSD分解结果 通过ICA对G(t)进行信噪分离,得到的源信号和噪声信号如图5所示。利用文献[12]的方法对相同的仿真信号处理,首先对故障信号进行EMD分解,根据峭度和相关系数对信号进行重构,利用ICA分离降噪,得到的源信号和噪声信号如图4所示。分别对由SSD-ICA与EMD-ICA方法得到的源信号Hibert包络解调,由图6可知,通过SSD-ICA方法降噪可以清晰的定位到故障特征频率的5倍频,频谱杂频成分减少,无关的影响被明显除去,而基于EMD-ICA只能定位到故障特征频率的4倍频,图谱中干扰成分较多,突出了SSD-ICA方法在滚动轴承故障提取上的优势。为了定量分析SSD-ICA、EMD-ICA两种方法降噪效果,通过峭度值和均方根误差值的大小进行评估。由表1可知,原始信号经SSD-ICA处理后得到的峭度值最大,说明冲击成分被凸显出来,噪声的影响明显降低,SNR的值也明显升高,可知SSD-ICA去噪效果更突出。 图4 仿真信号EMD-ICA分析结果 (a) 源信号 (b) 噪声信号图5 仿真信号SSD-ICA分析 表1 仿真信号降噪处理结果对比 图6 仿真信号包络分析结果 为了验证SSD-ICA方法在工程应用中可行性,对滚动轴承外圈故障的实验信号进行了分析。模拟滚动轴承故障的实验系统包括滚动轴承试验台、计算机、采集仪和加速度传感器,试验台包括交流电机、联轴器以及两个6206ZZ轴承等。数据采集具体参数设置为:电机转速1500 r/min,采样频率为96 kHz,采样点数为144 000。试验台的结构如图7所示,人为植入的轴承外圈故障如图8所示,表2为轴承的主要参数。 1.交流电机2.正常轴承3.转子4.故障轴承5.联轴器6.测功机 图8 外圈故障 表2 6206ZZ轴承的主要参数 图9 实验信号时域波形和频谱 对轴承外圈故障信号进行SSD-ICA分析,首先通过SSD将轴承外圈故障信号分解为6个SSC分量,如图10所示。各SSC同原始信号之间的相关系数值和峭度值,如表3所示。 图10 实验信号SSD分解结果 表3 SSC分量峭度和相关系数 根据表3选取SSC3分量和SSC4分量重构原始信号,用剩余其他4个分量构建虚拟噪声信号,将重构的原始信号和虚拟噪声信号组合成一个新矩阵输入到ICA中进行混解,得到源信号和噪声信号如图11所示。混解后信号的幅值发生变化,但对信号的分析并不产生影响。将实验数据进行EMD分解,同样根据峭度值和相关系数指标对原始信号和虚拟噪声通道信号重构,利用ICA分离降噪,可以得到源信号和噪声信号。分别将由SSD-ICA与EMD-ICA方法得到的源信号进行Hilbert包络分析,得到各自频谱如图12所示。由图12可知, SSD-ICA方法降噪可以清晰的定位到故障特征频率的3倍频,频谱干净,干扰信号被明显除去,相比于EMD-ICA方法故障特征频率二倍频的幅值已经较为微弱,由于噪声成分的存在三倍频完全被淹没。为定量对比EMD-ICA与SSD-ICA故障特征频率的提取效果,对比了两种方法前三倍频处的幅值,如图13所示。可以明显看出EMD-ICA前三倍频的幅值均小于SSD-ICA方法所得到结果的幅值,由此可以看出EMD-ICA在降噪效果上与SSD-ICA差距较大。 (a) 源信号 (b) 噪声信号图11 实验信号SSD-ICA分析 (a) EMD-FastICA (b) SSD-FastICA图12 实验信号包络谱分析 图13 倍频幅值对比图 针对振动信号受噪声干扰严重、故障特征提取较为困难的问题,提出了一种基于SSD-ICA的降噪新方法,并且将该方法应用在轴承的故障诊断中。通过仿真信号与实验数据证明了该方法的可靠性和优越性,并且得到如下结论: (1)采用SSD方法将信号分解,选择合适分量构建观测信号和虚拟通道噪声信号,解决了ICA算法在应用时信号数目欠定的问题。 (2)根据峭度和相关系数指标选择SSC分量,避免了分量选择的盲目性,选择合适分量构建观测信号和虚拟通道噪声信号,解决了ICA算法在应用时信号数目欠定的问题。 (3)SSD-ICA方法对复杂的振动信号降噪效果明显,可有效抑制背景噪声等干扰成分的影响。1.2 独立分量分析
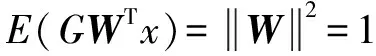
2 SSD-ICA的联合降噪方法
3 仿真信号分析
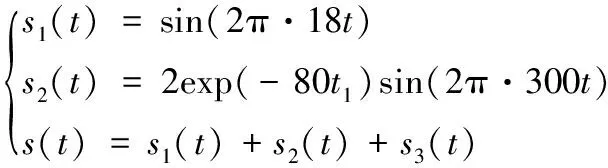
4 实验研究


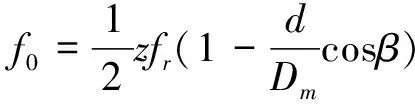
5 结论

