基于自我学习遗传算法的云制造资源优选*

宋士琳，赵 柱，薛 鹏，马沁怡，周茂军

(大连工业大学机械工程与自动化学院，辽宁 大连 116034)

0 引言

近年来，制造业逐渐由传统的线下交易模式转向线上交易模式，在信息技术和物流业的发展推动下，制造业倾向于开始外包其制造活动[1-2]。在此背景下，云制造(Cloud Manufacturing ,CMfg)作为新型网络化制造模式和集成技术正逐渐兴起，成为先进制造的重要发展方向[3-4]。CMfg环境下，如何提高制造服务效率与缩短制造服务时间一直是云制造亟需解决的问题[5]。通常借助各种智能算法来实现此类问题的解决与优化：文献[6]基于一种用作局部搜索的近似动态规划的遗传算法来解决动态泊位分配问题；文献[7]提出了一种新型的鲸鱼优化算法来解决云制造资源配置问题；文献[8]提出一种改进的带有精英策略的快速非支配排序遗传算法解决服务组合问题；文献[9]提出了一种高效的动态蚁群遗传混合算法，引入最优融合评价策略和迭代阈值加以改进。但上述文献中的单一智能算法在解决局部搜索问题上存在易陷入局部最优解且容易出现早熟的缺点，影响算法本身的搜索效率[10]，求解过程适应性不强，迭代求解过程的图像过于单调且极易陷入局部最优解，存在最优个体在迭代过程中淘汰的缺点。针对解决此类问题的特殊性，考虑到自我学习算法在解决全局优化问题上的特有优势，提出了基于Sarsa算法(一种自我学习算法)与遗传算法(Genetic Algorithm,GA)动态结合的算法对云制造资源优选方案进行动态优化的方法，通过建立以满足资源提供者相关效益与资源需求者任务需求为目标的数学模型，优化出云制造资源的优选方案，实现对总体完成时间的缩短以及云平台总体制造效率的提高。

1 制造资源优选数学建模

1.1 问题描述

建立结合实际制造需要以寻求最优配置的数学模型并通过建模求解与实例验证，并作如下假设：

(1)资源需求者的需求可分解为多个子任务。

(2)一个子任务的制造资源只能由一个资源提供者提供，每个资源提供者可同时处理多个子任务。

设n个资源需求者(Cus)的若干子任务(Tas)有l个资源提供者(Sup)提供制造资源，相关参数及描述见表1。

表1 相关参数符号及描述

1.2 目标函数

(1)时间成本目标函数

制造服务的时间类别包括制造时间和运输时间，则时间函数[11]表示为：

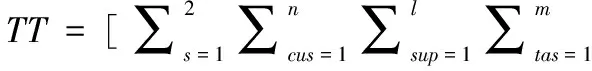
(1)

式中,n为资源需求者数量，l为资源提供者数量，m为单个资源需求者的子任务数量，其中匹配资源提供者具有唯一性：

mat(sup,cus,tas)=1,0

(2)

式(2)表示若资源提供者sup与资源需求者cus的子任务tas相匹配，则mat(sup,cus,tas)=1，反之mat(sup,cus,tas)=0。

t(sup,cus,tas,1)=mt(sup,cus,tas)

(3)

t(sup,cus,tas,2)=tt(sup,cus,tas)

(4)

(2)资源提供者效率转化函数

资源提供者效益转化函数[12]表示为:

BR=

(5)

(3)整体目标函数

为实现可接受条件下的多目标要求，赋予各目标不同的权值从而达到资源方案的非劣性平衡。此函数可表示为：

(6)

式中，ω1、ω2分别为时间函数和效益函数的权值,j=1,2,3...l。

1.3 约束条件

各子任务时间之和不超过该任务最大时间：

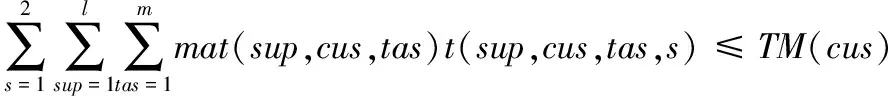
(7)

2 模型求解

2.1 染色体编码

采用整数编码，每个染色体表示待选任务的全部制造顺序。染色体长度为2 m。定义前半段为所有资源需求者编号，数量即表示子任务的数量；后半段表示前半段资源需求者的子任务对应的资源提供者编号。

以某条染色体为例，见表2。

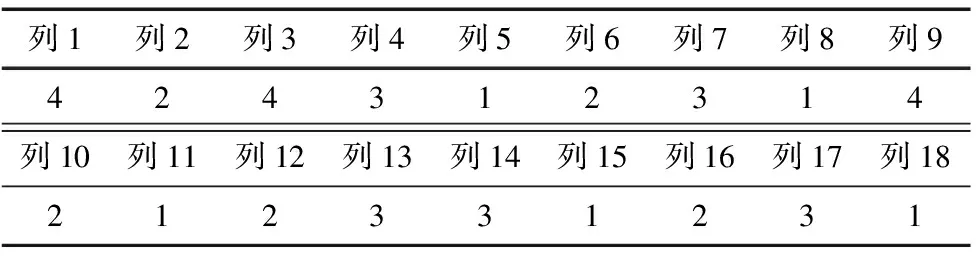
表2 染色体编码

表2中列数表示该条染色体包含基因数，共18列，每一列表示一个基因。该条染色体个体表示4个资源需求者分别包含2,2,2,3个子任务在3个资源提供者进行生产制造。

2.2 种群初始化

随机生成N个初始染色体个体，这N个个体组成一个种群，以这N个个体构成的种群作为初始种群，逐代进化，设置t=0，最大进化代数为gen。

2.3 适应度值

适应度函数值是评价个体优劣的指标[12]：

(8)

式中，常数c为保守估计值，视目标函数而定，P表示整体目标函数值。

2.4 选择操作

采用轮盘赌的方式对个体进行选择。每个个体的适应度值与整个种群中个体适应度值和的比例决定进入下一代的概率[13]：

x(i)=Fit(i)/∑Fit(t)

(9)

2.5 基于Sarsa算法自我学习的交叉和变异操作

设交叉率与变异率分别为Pc和Pm，Pc与Pm过大或过小都会对破坏种群，不利于解的收敛和最优解的生成;本文设计了一种能够根据迭代进程进行自我学习的动态参数生成方法，实现智能调整遗传算法的关键参数，自我学习的模型框架如图1所示，在时间步长t时，代理获取当前状态st并在at采取行动。然后，在第t+1时刻，转入状态st+1,代理从环境中得到奖励rt，代理更新动作选择并采取合适的动作。

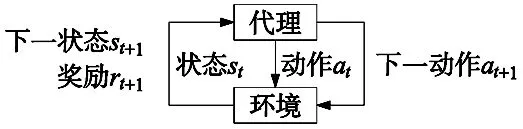
图1 自我学习框架

图中t是当前步,S集包含所有状态。Sarsa算法的目标是估计一个最优策略的Q值。该模型根据环境和状态行为的反馈信息进行更新，用以表征行为选择的合理性。Q值保存在Q值表中，用于记录学习经历。初始Q值表(式10)是一个零值矩阵，其行数等于状态的数量，列数等于动作的数量。Q值的计算需要考虑已有的状态、行动、奖励等经验, 式(11)为Q值更新算法。

(10)

Q(st,at)←(1-α)Q(st,at)+α((rt+1+γQ(st+1,at+1))

(11)

式中，Q(st,at)表示在当前状态st执行行为at后的Q值;α表示学习率，设为0.75;rt+1表示在状态st执行行为at后的奖励价值，初始奖励r= 1;γ表示折算率，设为0.2；Q(st+1,at+1)表示在状态st+1下通过ε-贪婪决策选择的行为at+1的期望Q值。

主要步骤[14]：

步骤1:初始化Q值表；

步骤2:获得当前状态st，s←st；

步骤3:根据Q值表选择动作a并执行；

步骤4:获得强化奖励r，并获得新的状态st+1；

步骤5:如果满足GA的停止条件，则终止进程，否

则转到步骤6；

步骤6:根据式(11)更新Q值；

步骤7:更新状态:s←st+1，转到步骤2。

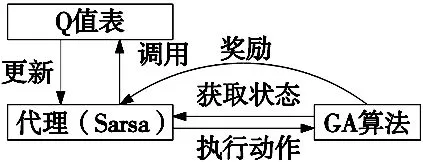
图2 学习模块

2.5.1 状态与行为设置

状态的构建需要考虑种群适应度的变化，包括：种群平均适应度、种群多样性、最佳个体适应度。式(12)表示用第一代种群的平均适应度标准化后的种群平均适应度；式(13)表示第一代种群多样性归一化后的种群多样性；式(14)表示用第一代的最佳适应度进行归一化后得到种群最佳适应度[15]；式(15)表示种群状态值：

(12)

(13)

(14)

S*=w1f*+w2d*+w3m*

(15)

2.5.2 奖励方法

通过最优个体适应度与种群平均适应度转换计算得出奖励值。式(16)表示Pc奖励，式(17)表示Pm奖励。如果第t代的最优个体优于第(t-1)代，代理就会得到当前Pc有效的奖励。如果第t代的平均适应度优于第t-1代，代理会得到当前Pm有效的奖励。

(16)

(17)

2.5.3 行为选择策略

在探索和开发之间进行行为选择。ε-贪婪是一种行为选择策略,式(18)表示在获取到状态s后对行为a的决策[16]：

(18)

式中，ε为贪婪率，取ε= 0.9，β是0到1之间的一个随机值。当ε≥β，使期望Q值最大化的动作a被选择，这也被称为贪婪策略。当ε<β时，进行探究，选择一个随机动作a。

2.5.4 交叉与变异操作

基于Sarsa算法改进的遗传算法(以下简称Sa-GA)中，每一次的迭代都需要获取自我学习代理中的Pc和Pm值，进行交叉与变异。

在被选中的变异个体中，首先确定变异位置P1、P2，然后把相应位置的子任务或制造资源提供者进行对换，即实现个体的变异。

当满足最大迭代次数时，运算终止，输出结果，得出最终的优化结果，总体流程图如图3所示。

图3 基于Sarsa改进的GA算法运算流程图

3 案例验证与分析

3.1 案例描述

对本文的基于Sa-GA的制造资源优选方法进行验证。模拟某时段某云制造平台运营状况:10家资源提供者与6名资源需求者的需求申请，将每个需求分解为11个子任务，匹配关系与时间成本如表3所示。

表3 任务可选方案

表中可提供服务的制造商数量为1～2个，括号中为对应的制造时间，若无相对应任务，则时间为0。

3.2 算法验证分析

以表3数据为输入的问题模型对时间目标函数进行有效验证。相关参数设置如表4所示。

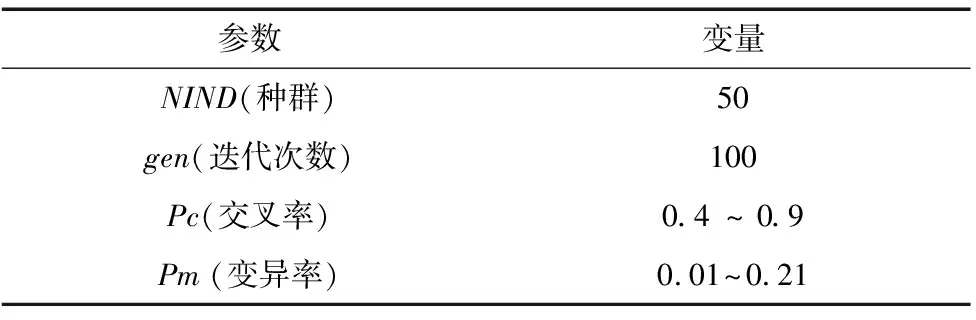
表4 相关参数设置

取各制造资源提供者的效益转化率br(sup=i，i=1,…,10)分别为：96%，95%，93%，92.5%，96%，98%，95%，96.5%，97%，94%，代入式(4)得到资源提供者效益值，见表5。

表5 资源提供者效益值

优化步骤如下：

步骤1：初始化表4中遗传相关参数。初始化表3相关数据与自我学习状态设置和行为设置；

步骤2：据式(5)，计算个体适应度值并对个体根据适应度值进行排序，选出优秀个体；

步骤3：据式(9)进行选择，采用前半段基因的单点交叉并按每次迭代经Sa-GA生成的交叉率Pc与变异率Pm随机选择进行交叉与变异操作；

步骤4：将新个体重新插入种群，进行循环；

步骤5：达到最大迭代次数时停止，返回最优值。

最后得出解的收敛曲线，见图4，Sa-GA对云制造资源优选的解的收敛在迭代前半段达到相对稳定趋势后仍然能继续找到相对更优解，对比GA对资源优选解的收敛在前半段趋于固定值后没有继续更新，其已陷入局部最优解或已淘汰最优个体，说明Sa-GA对寻优过程有较有效的优化。Sa-GA云制造资源优选方案如图6所示,对比GA(图5)，最短完成时间分别在80～85天之间与90～95天之间，完成时间大幅减少，说明Sa-GA对目标函数的寻优程度有显著的提升。

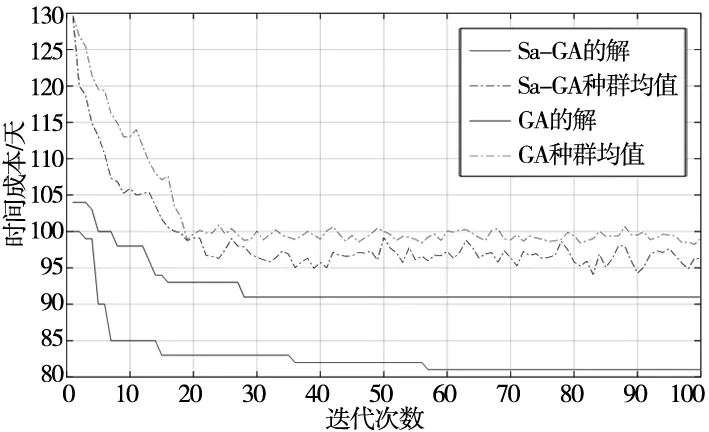
图4 Sa-GA与GA进化收敛曲线对比

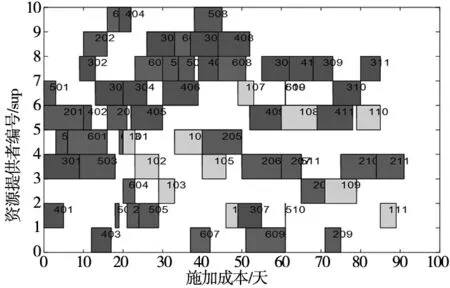
图5 GA资源优选方案

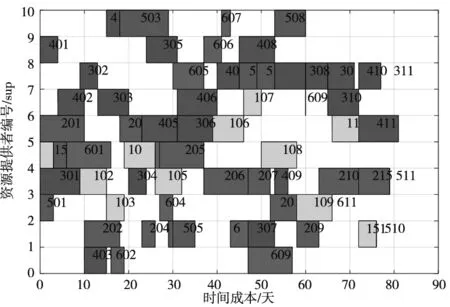
图6 Sa-GA资源优选方案

4 总结

针对云制造环境下多制造任务并行情况下的资源优选，本文提出了一种资源优选方法，该方法以制造资源的时间成本与使用效益为优化目标，应用基于Sarsa算法改进的遗传算法经自我学习实现相关参数动态化优化，避免了因单一算法过早收敛或陷入局部最优而影响整体的优化配置方案，通过实验验证该模型优化方法明显提高了云制造环境下资源提供者的生产效率，有效缩短了订单完成时间。