基于自适应经验小波分解和深层Wasserstein网络的轴承工况识别*

左大利

(东莞职业技术学院机电工程学院，广东 东莞 523808)

0 引言

滚动轴承是旋转机械的重要部件之一，对于保证整机的运行安全，具有重要意义[1]。目前，基于传感器物理量的轴承工况识别方法应用最广泛，且研究最多的是振动信号，然而，实际采集到的轴承振动数据往往受环境噪声干扰，且出现一定的非线性和非平稳性。因此有必要对轴承振动数据进行预处理以获得更好的工况识别结果。

传统基于“特征提取+模式识别”的轴承工况识别方法很大程度上依赖于繁琐的人工特征提取和特征选择，受主观影响较大。深度学习[2]能自动从信号中学习有价值的特征，在轴承工况识别领域取得了较大突破[3]。周兴康等[4]构建一维残差自编码神经网络对旋转机械进行工况识别，实验结果表明提出网络具有良好的工况特征提取能力；张鑫等[5]将流形学习与深度置信网络用于轴承工况识别，在不平衡的数据集下也实现了很好的识别效果。但上述研究表明，振动信号噪声的存在会降低深度学习模型的工况识别准确率和收敛速度[6]。然而，EMD[7]、EEMD[8]、LMD[9]等模态分解降噪方法缺乏严格的理论基础；VMD[10]的分解模态个数难以确定；经验小波分解(empirical wavelet decomposition，EWD)[11]具有完备的数学理论，分解结果较稳定，但其频谱边界难以划分。

本文针对EWD和深度学习的优势，提出一种基于AEWD和DWN的滚动轴承工况识别方法，实验结果表明该方法具有较好工况识别效果。

1 自适应经验小波分解

EWD通过对信号的谱边界进行检测和分割，然后利用小波提取相应频段的调幅-调频成分，但目前存在的谱边界检测方法均存在较大的缺陷[11]。轴承振动信号经常受到环境噪声的干扰，进而淹没信号中包含的工况特征，从而降低工况识别准确率。考虑到轴承振动信号频谱中的噪声在幅度上往往比有效频率分量小，因此提出一种基于频谱包络的边界分割方法，并据此进一步确定EWD分解模态数，详细步骤如下，流程图如图1所示。

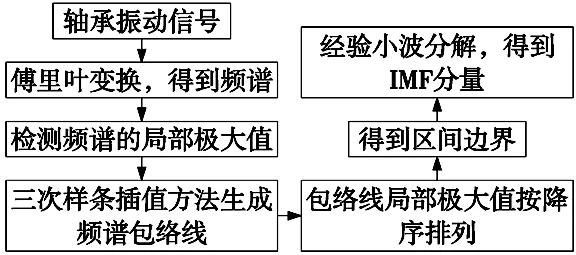
图1 频谱包络的边界分割方法

步骤1：对轴承振动信号x进行傅里叶变换。

F(s)=FFT(x)

(1)

Mx=|F(si)|(i=1,2,...,l)

(2)

式中，l等于信号x维度的一半。

步骤2：检测Mx的局部极大值。

步骤3：使用三次样条插值方法生成频谱的包络线。

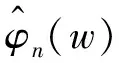
(3)

(4)

重建公式如下：

(5)

式中，*代表卷积操作，则信号f(t)可被分解为：

(6)

(7)

式中，k=(1，2，...，N-1)。

2 深层Wasserstein网络

变分自编码器(variational auto-encoders，VAE)是一种无监督学习模型，相比于自编码器和限制玻尔兹曼机更适合处理大量的滚动轴承振动数据，但VAE训练困难，学习到的隐层特征比较模糊，难以刻画真实滚动轴承振动数据分布的多样性[12]。Wasserstein自编码器(Wasserstein auto-encoder，WAE)将VAE和生成对抗网络(generative adversarial network，GAN)的优势结合，能描述轴承真实振动数据分布的多样性，且易于训练。设编码器为Q，解码器为G，输入数据X的概率分布设为PX，设隐层编码特征Z的先验分布为PZ，重构输入数据的概率分布为PG，由隐层编码特征Z生成X的生成模型为PG(X|Z)，由数据X生成隐层编码特征Z的编码模型为Q(Z|X)。VAE和WAE的模型架构分别如图2和图3所示。

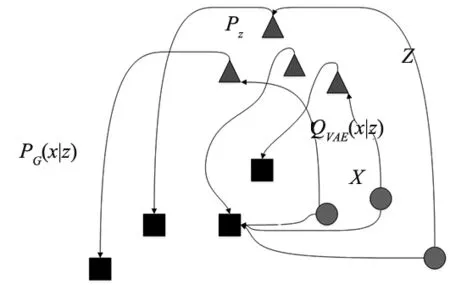
图2 VAE架构

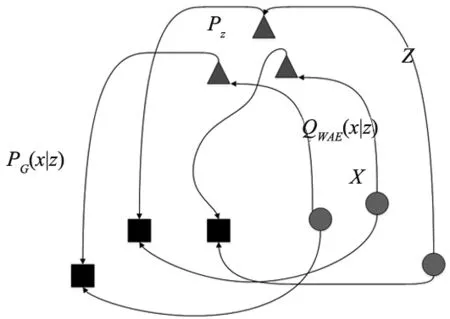
图3 WAE架构

三对从PX中取样的输入样本x，VAE使Q(Z|X=x)匹配PZ(图2圆形为QZ，蓝色三角形为PZ)；相反，WAE使QZ匹配PZ(如图3圆形)，进而使不同样本的隐层编码特征相距较远，以便更好的进行重构。WAE的目标为最小化重构损失，即衡量输入数据的概率分布PX和重构数据的概率分布PG之间的距离。本文使用最优传输距离(optimal transport，OT)，OT的定义如下：

(8)

式中，c(X,Y)为损失函数，本文采用文献[12]提出的简化版OT损失函数，如下：

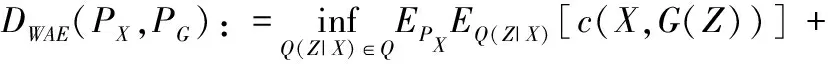
(9)

式中，编码器Q和解码器G的参数由深层神经网络估计；DZ(QZ,PZ)为最大均值误差(maximum mean discrepancy，MMD)的正则项，令DZ(QZ,PZ) =MMDk(PZ,QZ)，则MMDk(PZ,QZ)通过下式计算：

(10)

式中，k()为再生核函数，具体见文献[12]。

深层Wasserstein网络(DWN)堆叠多个WAE，能进一步提高网络学习到的特征的质量。首先，利用无标签的轴承振动数据训练第一层WAE，得到第1隐层特征；其次，将第1隐层特征输入第2层WAE，得到第2隐层特征；以此类推；最后，利用少量带标签样本对整个DWN进行有监督微调，如图4所示。

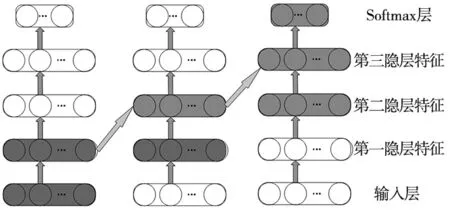
图4 DWN结构

综上所述，AEWD结合DWN的轴承工况识别步骤如下，工况识别流程图如图5所示。

(1)采集不同工况下的滚动轴承振动信号，随机选取80%作为训练样本，其余为测试样本；

(2)对样本进行AEWD分解，并利用综合评价指标对本征模态分量进行信号重构；

(3)将重构后的训练样本输入DWN进行无监督预训练和有监督微调；

(4)使用测试样本对训练好的网络进行测试。

3 实验验证

3.1 实验数据描述

为验证提出算法的有效性，以XJTU-SY轴承数据集[13]为对象，其轴承试验台如图6所示。限于计算资源，本文在XJTU-SY数据集中选取7种不同的轴承运行工况，见表1所示。7种轴承运行工况的时域图和频域图如图7所示，可知信号受噪声干扰严重，难以对轴承运行工况进行有效区分。

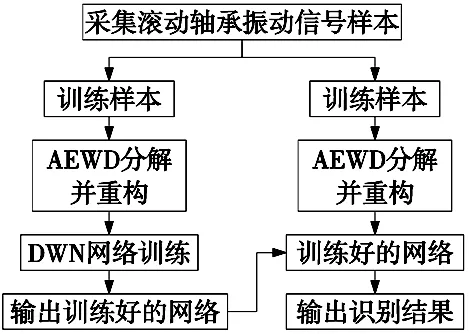
图5 工况识别流程图

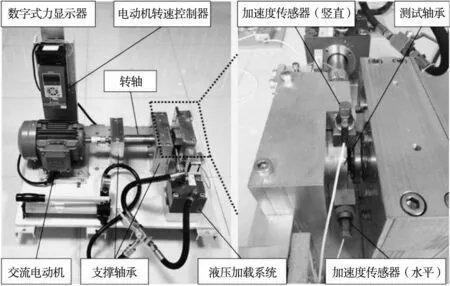
图6 轴承测试实验台

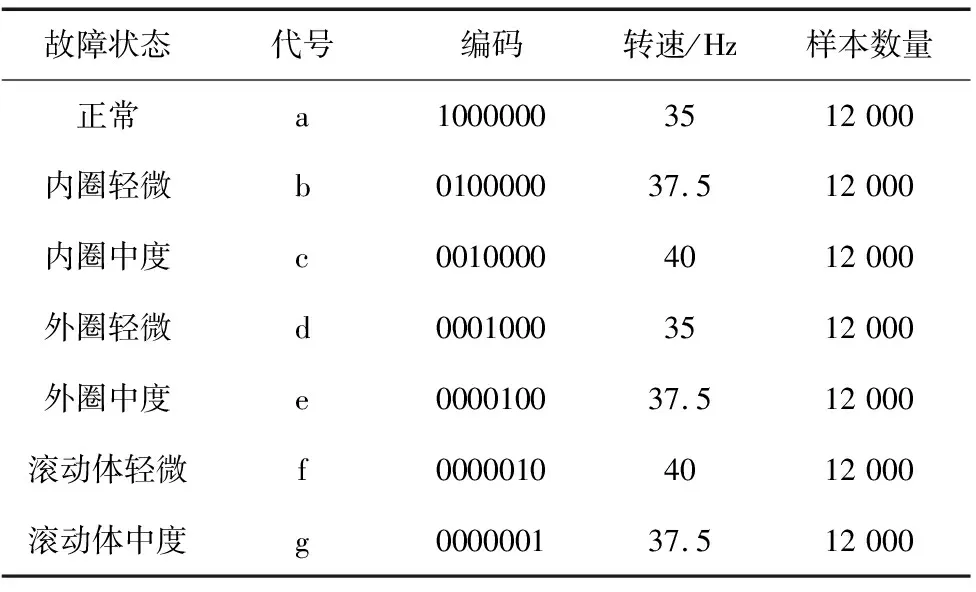
表1 7种滚动轴承工况

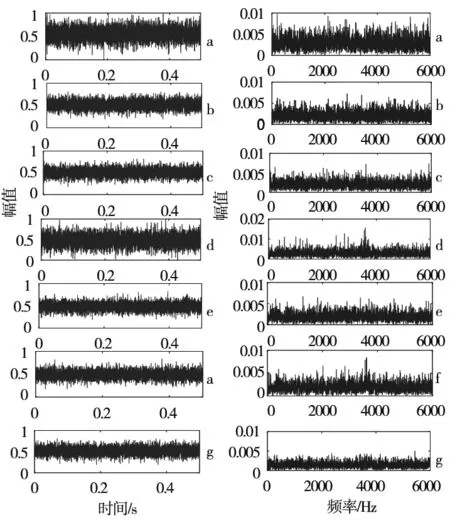
图7 滚动轴承7种工况的时域图和频域图

3.2 综合评价指标

本文使用综合评价指标，表达式如下：

P=ηKr+φrxy+ξexy

(11)

η+φ+ξ=1

(12)

式中，φ，η，ξ为比例系数，0<φ，η，ξ<1。Kr为峭度，表征信号中的冲击成分；rxy为相关系数，表征各模态分量与原始信号的相关程度；exy为能量比，表征分解结果的能量泄漏程度。经反复实验，取各指标为相同权值，选择P最大的前4个分量进行重构。

3.3 实际信号分解效果对比

以表1轴承外圈轻微故障信号为例，分别采用AEWD和原始EWD对其进行分解，如图8和图9所示。可见，原始EWD分解结果模态混叠严重，干扰过多，根据综合评价指标P，对信号重构并进行相应的时频变换，如图10和图11所示。

由式(13)计算求得轴承外圈故障特征频率约为100 Hz。

(13)

式中，d为滚子直径，D为节圆直径，a为接触角，Z为滚子数，fr为转频30 Hz，从AEWD时频谱中可以比较清晰的看出故障外圈故障频率以及倍频，验证了AEWD的有效性。

图8 AEWD分解结果

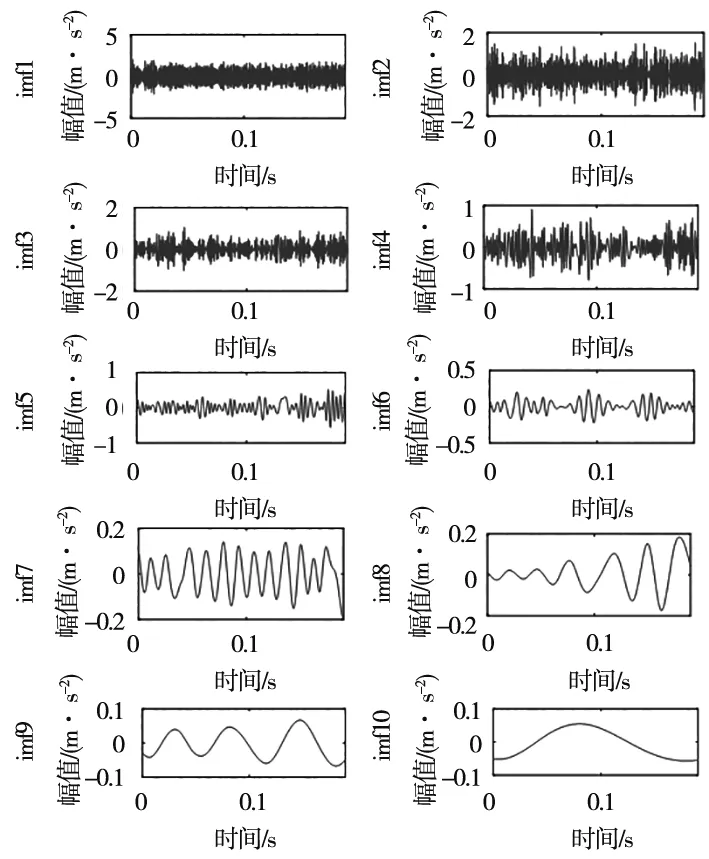
图9 原始EWD分解结果

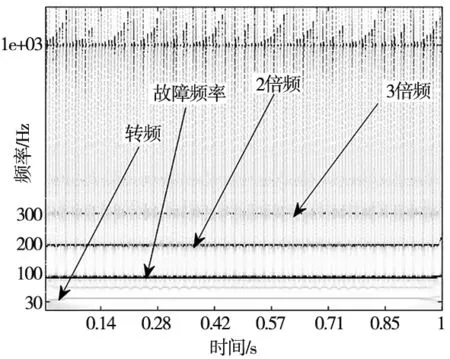
图10 AEWD时频图

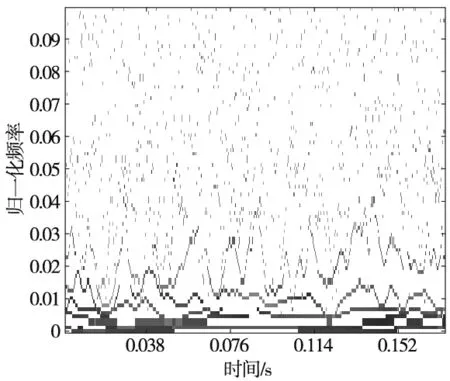
图11 原始EWD时频图

3.4 工况识别与分析

为证明AEWD-DWN模型的优越性，采用多隐层自编码网络(multi hidden layers auto-encoder network，MHLAEN)、多隐层稀疏自编码网络(multi hidden layers sparse auto-encoder network，MHLSAEN)、多隐层降噪自编码网络(multi hidden layers denoising auto-encoder network，MHLDAEN)、多隐层变分自编码网络(multi hidden layers variational auto-encoder network，MHLVAEN)等方法进行对比分析，各方法的详细参数如下。

本文方法(AEWD-DWN)：DWN初始结构为1024-512-256-128-64-32-7，每个WAE的学习率为0.05。

方法2(AEWD-MHLAEN)：MHLAEN结构为1024-512-256-128-64-32-7，每个自编码器的学习率为0.05。

方法3(AEWD-MHLSAEN)：MHLSAEN结构为1024-512-256-128-64-32-7，每个自编码器的学习率为0.05，稀疏因子为0.05。

方法4(AEWD-MHLDAEN)：MHLDAEN结构为1024-512-256-128-64-32-7，Dropout率取0.2，每个降噪自编码器的学习率为0.05。

方法5(AEWD-MHLVAEN)：MHLVAEN结构为1024-512-256-128-64-32-7，每个VAE的学习率为0.05。

方法6(EWD-DWN)：与方法1不同的是，信号前处理方法采用原始EWD。

方法7(CEEMD-DWN)：与方法1不同的是，信号前处理方法采用互补集合经验模态分解(CEEMD)。

表2列出了各方法10次实验的平均识别精度和用时。

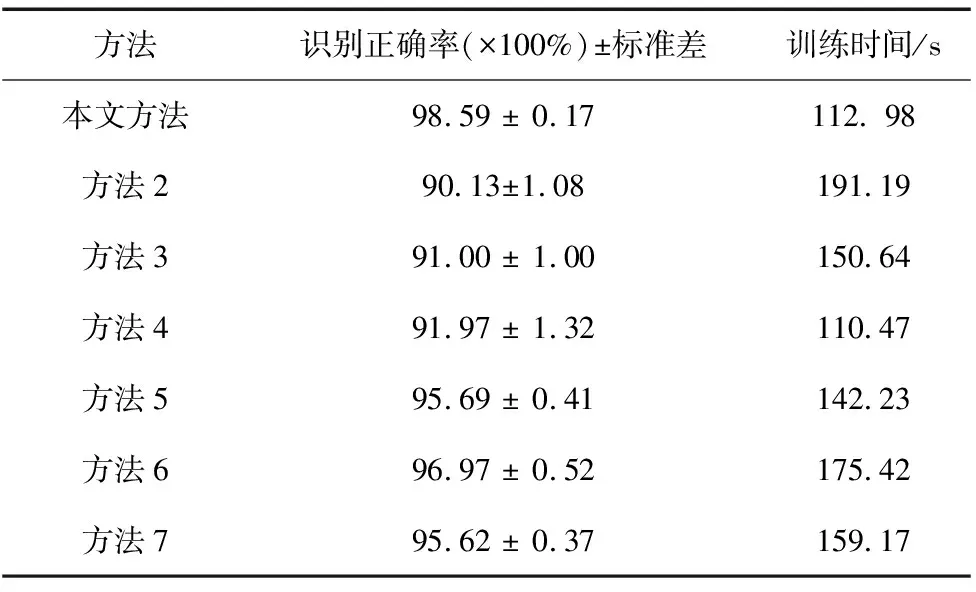
表2 不同方法的识别结果

由表2知，AEWD-DWN模型具有更高的识别准确率(98.59%)和更小的标准差(0.17)，MHLAEN的工况识别率最低；MHLSAEN的稀疏项限制可有效提取输入信号的较重要的信息；MHLDAEN的降噪机制提高了网络对噪声的鲁棒性；MHLVAEN将输入轴承振动信号映射为一组特殊的概率分布，再从概率分布中随机采样得到隐层特征，提高了对环境噪声的鲁棒性。方法6和方法7分别利于原始EWD和CEEMD对振动信号进行前处理，由于原始EWD和CEEMD的模态混叠缺陷，导致组合模型的工况识别率低于本文方法。

3.5 不平衡数据集下AEWD-DWN的识别准确率

实际情况下正常样本所占比例通常较高，为验证AEWD-DWN模型在面对不平衡数据集时的有效性，设计4种数据集，设置正常与各故障工况的训练样本比例分别为12 000：10 000、12 000：8000、12 000：6000和12 000：4000。本文定量计算几种方法基于不平衡数据集的精确率(P)、召回率(R)和F1值：

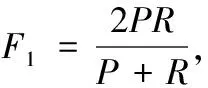
(14)

式中，TP为正样本中被模型判断为正的个数，FP为在负样本中被模型判断为正的个数，FN为正样本中被模型判断为负的个数，F1值在[0，1]之间，反映查准率和召回率的信息，0代表最差，1代表最好。以组4为例，表3列出了组4中3种方法的精确率和召回率，表4列出了相应的F1值。

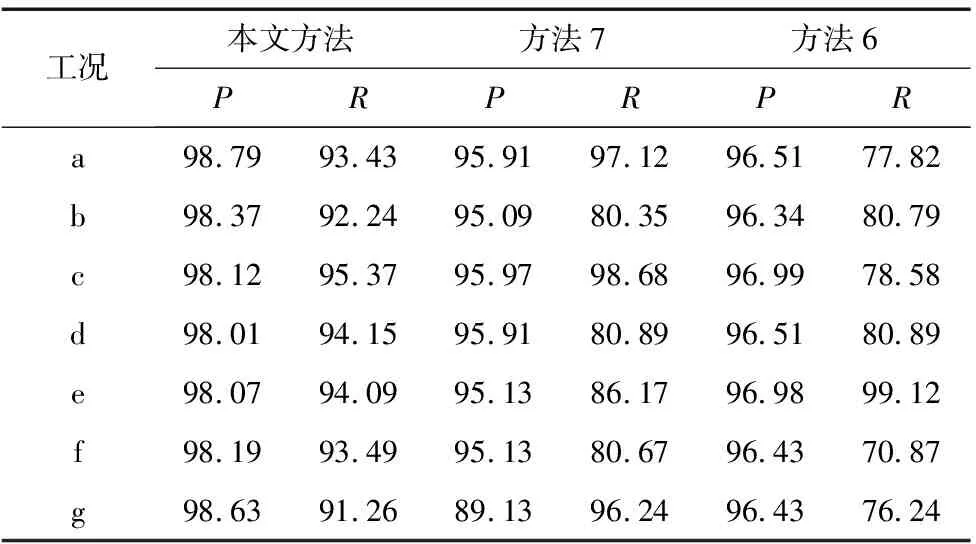
表3 组4不同方法的精确率和召回率

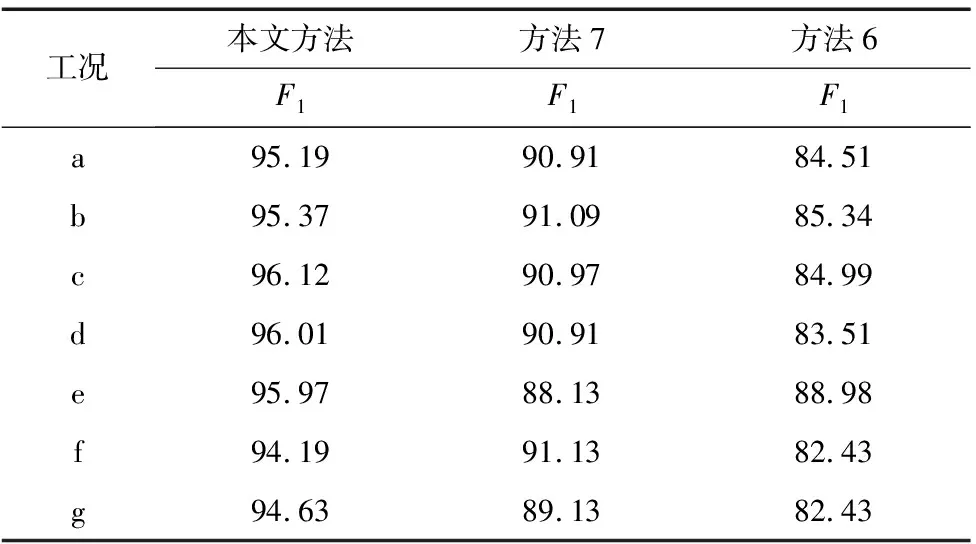
表4 组4不同方法的F1值

由表3和表4可知，组4中本文方法的P、R和F1指标值均较高，类似的结果在其他组中也有较为明显的体现，这些对比结果进一步验证了AEWD-DWN在面对不平衡数据集时的有效性。

4 结论

本文提出一种基于AEWD-DWN的滚动轴承工况识别方法，主要结论如下：

(1)提出一种自适应经验小波分解(AEWD)方法，使用三次样条插值方法生成轴承振动信号频谱的包络线，然后进行自适应分割，进而利用小波函数提取IMF分量，最后利用综合评价指标进行imfs的选取并重构。AEWD方法相比于原始EWD方法能更有效地避免模态混叠现象，其时频谱图更加清晰，时频分辨率更高。

(2)将DWN引入滚动轴承工况识别领域，其将变分自编码器和生成对抗网络结合，更能比较真实的描述轴承振动数据分布的多样性，相比于变分自编码易于训练，能有效避免“模型崩塌”现象，实验结果表明以DWN或VAE为主的深层概率生成模型将是机械故障识别的方向。