圆盘锯齿刀超声切削Nomex蜂窝芯力热分析*

袁信满，赵清泉，鄢旭东，候天齐，宁海峰，王贵鑫

(1．成都飞机工业(集团)有限责任公司，成都 610092；2.西南石油大学机电工程学院，成都 610500)

0 引言

薄壁多孔结构的Nomex 蜂窝芯复合材料因其高比强度，低密度，耐腐蚀，热稳定性好等优异的材料性能被广泛应用于航空航天中[1-2]，但航空航天领域的机械零部件多为复杂曲面结构，因此Nomex蜂窝芯复合材料的二次切削加工是必要的。但其各向异性的特点使之在切削过程中常出现蜂窝断裂、压塌、加工面毛刺等问题[3]。

为改善由于蜂窝芯复合材料特殊结构特性带来的切削加工缺陷，超声切削加工技术被应用于其二次成型加工中，通过超声振动使刀具与材料的作用机制发生变化，有效地提高了材料去除率，减少了刀具磨损，极大程度改善了加工质量[4]。

蜂窝复材与其切削刀具价格昂贵，仅通过实验探究其机理会耗费大量成本，因此实验与仿真相结合是较优的分析方法。方亮[5]通过有限元分析刀具在切削力作用下的应力变化，优化刀具结构，加工出表面光滑的蜂窝芯型面。牛景露等[6]通过试验的方式采集Nomex蜂窝芯超声切削的切削力，通过回归分析推导出在不同切深和振幅下的切削力的经验公式。张生芳等[7]分析刀具结构参数对Nomex蜂窝芯复合材料切削力和切削温度的影响规律，为刀具的结构优化提供参考。何畏等[8]对不同楔角锯齿圆盘刀建立动力学模型，利用仿真软件进行模态分析，为刀具的研发提供了参数支持。李秀渊等[9]以不同建模方式分析材料模型对蜂窝材料超声切削过程仿真的影响。

目前的研究大多集中于圆盘锯齿刀具结构与切削力、切削质量之间的影响关系，关于切削参数对切削力热的影响研究甚少。本文通过有限元仿真软件，建立圆盘锯齿刀切削Nomex蜂窝芯复合材料有限元模型，并与实验相结合，分析主轴转速n、进给速度vf以及切削宽度ae和切削深度ap四切削因素与切削力热的影响关系，建立中心复合实验方案，得到切削温度与进给速度、主轴转速一次回归模型，对于切削过程的工艺优化有一定技术参考价值。

1 有限元模型

1.1 刀具与材料模型

(1)圆盘锯齿刀

超声切削Nomex蜂窝芯材料精加工与传统金属切削加工存在较大区别，所用刀具边缘刀刃处有楔角结构形成锋利刃口，使蜂窝芯材料更加容易被切断，圆盘锯齿刀基本结构如图1所示。刀具直径：50.8 mm,楔角：14°,刀具高度：5 mm,刀具内孔直径：12 mm。

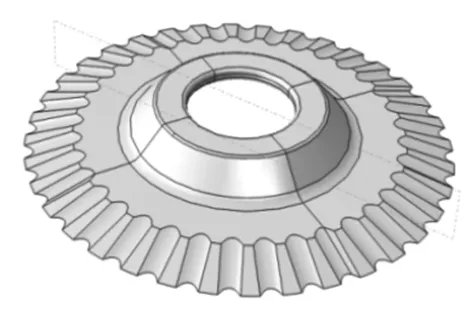
图1 圆盘锯齿刀基本结构

表1 锯齿刀材料属性

(2)Nomex蜂窝芯

Nomex蜂窝芯是一种正六边形多孔薄壁的各向异性材料，具体结构如图2所示，芯格边长3 mm，单层和双层芯格厚度分别为0.1 mm和0.2 mm。模型几何尺寸为60 mm×20 mm×15 mm。

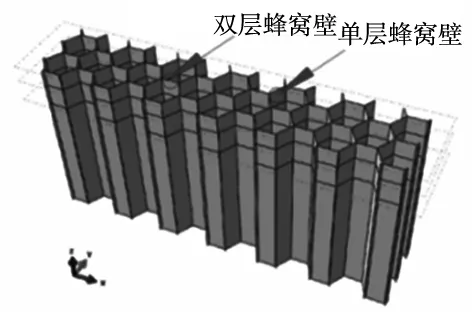
图2 Nomex蜂窝芯几何模型图

Nomex蜂窝芯材料属性如表2所示。

表2 Nomex蜂窝芯材料属性

1.2 材料失效准则

由于蜂窝芯材料的独特性，采用弹塑性模型剪切失效Shear Failure准则，通过判断单元节点的塑性应力是否达到塑性极限值来建立剪切失效模型。塑形极限值也称之为破坏系数ω，破坏系数达到1时材料失效，形成切屑，破坏系数ω可定义为：

(1)

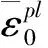
1.3 网格划分及边界条件

本文使用Hypermesh软件对圆盘刀加工路径上的蜂窝芯材料进行局部细化和尖锐处理。将划分好的蜂窝芯导入Abaqus中，考虑到切削热的计算，因此选用温度-位移显式算法。对Nomex蜂窝芯采用C3D8T八结点热耦合六面体的网格划分，圆盘刀采用 C3D10MT结点网格划分。仿真过程中，圆盘刀刚度远大于蜂窝芯刚度，因此仿真过程中将刀具作为刚体。摩擦系数为0.2。在仿真模型中，假设零件固持牢固，对于零件底面的所有节点均采用完全固定。设置零件、圆盘锯齿刀和环境的初始温度为室温。圆盘刀超声振动切削Nomex蜂窝芯仿真模型如图3所示。

图3 圆盘刀超声振动切削Nomex模型

刀具施加3个方向的运动载荷：刀具自身旋转；沿x方向的进给运动；z方向的振动。仿真加工工艺参数如表3所示。

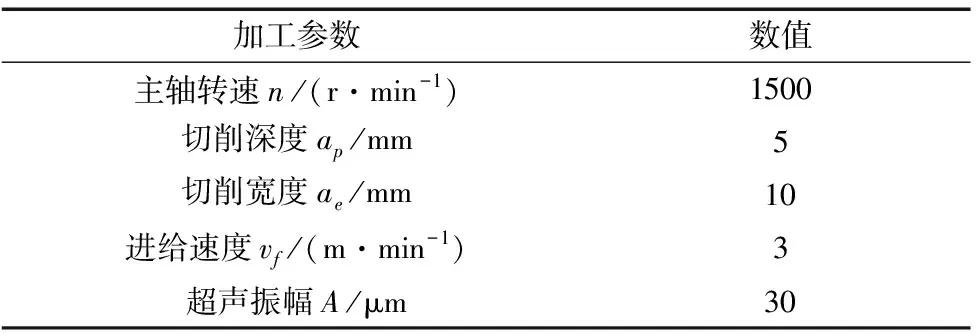
表3 圆盘锯齿刀仿真加工参数

2 实验设计

实验以主轴转速n、进给速度vf以及切削宽度ae和切削深度ap四切削因素为主要研究对象，在超声振幅A=30 μm工况下设计单因素实验，为保证仿真与实验一致，先用尖形刀在待加工层切削出圆盘刀将加工的厚度和宽度，再用圆盘刀加工出需要的零件型面。

重庆自贸区属于中国自由贸易区的一部分，是我国政府设立的区域性自由贸易园区，致力于将其建设成为服务于“一带一路”建设和长江经济带发展的口岸高地和国际物流枢纽，以建设一个投资贸易便利、金融服务完善、高端产业集聚、法治环境规范的高水平自由贸易园区为发展目标。因此，加强重庆自贸区知识产权保护，对于推动重庆自贸区建设，全面深化改革、扩大开放等都具有重要作用和深远意义。

实验采用Kistler传感器接收切削力信号并转换为微小电压信号，与传感器配套的电荷放大器将其放大后传入计算机终端形成切削力数值信息。在开展试验时，每一组工艺参数进行两次切削加工实验，并取其平均值，Nomex蜂窝芯复合材料切削实验原理如图4所示。

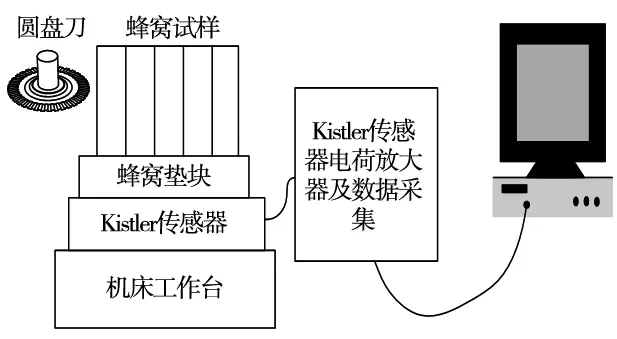
图4 实验原理图

3 仿真结果分析

图5、图6为表3仿真加工参数下的切削应力云图，切削初期(如图5)，刀具逐步将材料破坏，圆盘刀在高速旋转的同时逐渐进给与蜂窝材料接触，带有锯齿状的刀片开始挤压切断第一层蜂窝壁，直至刀片完全切入材料。

图5 切削初期

稳定切削阶段，圆盘刀在超声振动运动与旋转运动相结合的情况下稳定撕裂并切削蜂窝芯，切屑形状保持完整，不易碎裂。在图6稳定切削阶段，圆盘刀沿进给方向逐渐切离蜂窝芯，切屑分离，直至刀具完全离开。在整个切削仿真加工过程中，蜂窝芯与圆盘刀一直处于接触状态。被加工的蜂窝芯所受到的Mises应力值最大约为97 MPa；切屑与已加工蜂窝表面分离后仍然有残余应力的存在，约为48 MPa。

图6 稳定切削阶段

4 实验数据分析

4.1 切宽对切削力热的影响

三向切削力随着切削宽度的变化如图7所示，随着切削宽度从4 mm增加到20 mm，X、Y、Z三个方向的切削力实验值分别提高了2.52倍、2.77倍和2.22倍，仿真值分别提高了2倍、2.69倍和2.14倍，切削力仿真结果趋势与实验结果趋势基本一致。其中切削力实验值均比仿真值略大。这是由于仿真过程中一些单元断裂后直接删除导致。从总的变化趋势来看，切削宽度的增大会导致切削面积增大，进而导致切削力增大。

如图8所示，随切削宽度的增大，圆盘刀切削温度呈缓慢增长趋势，这是由于切削宽度的增长虽然会使圆盘刀切入蜂窝芯接触面积增大，产生热量增多，但是在切削区参与切削的刀刃数和切削长度同时会逐渐增多，加快了热量的散失，最终导致刀具温度上升不明显。

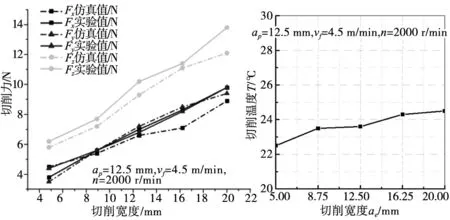
图7 三向切削力随切削 宽度的变化曲线 图8 切削温度随切削 宽度的变化曲线

4.2 切深对切削力热的影响

在控制单一变量情况下，切削力随着切削深度的增加而呈增大的趋势，但整体增大的幅度不大。三向切削力变化如图9所示。由于切削深度对刀具与工件表面的接触面积的影响不大，切削深度的增加仅仅增加了刀具对蜂窝材料上下撕扯的程度。三向切削力的实验值与仿真值最大误差分别为8.4%、6.4%和11.2%。切削温度随切深涨幅不大，情况与切宽相似。如图10所示。

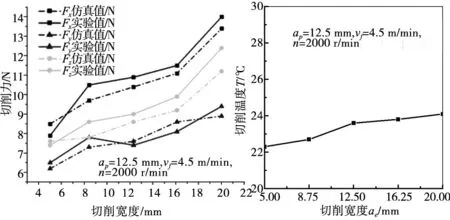
图9 三向切削力随切削 深度的变化曲线 图10 切削温度随切削 深度的变化曲线

4.3 进给速度对切削力热的影响

在控制单一变量情况下，三向切削力随进给速度的增大而逐渐增加，如图11所示，但增加幅度不大。由于Nomex蜂窝芯独特的多孔结构使得切削力大大减小，进给速度的增大只会导致刀具切削蜂窝壁的切削力有小幅增大，但是其前提是需要保证蜂窝芯能固持可靠，现场加工表明，如果固持工艺可靠，进给速度可达到30 m/min。当进给速度从3 m/min～6 m/min范围内逐渐增大，三向的切削力实验趋势与仿真趋势保持一致。

如图12所示，进给速度从3 m/min～6 m/min范围内，切削温度随之从21.5 ℃升高到28.8 ℃。这是由于提高进给速度，单位时间内刀具材料间的接触面积增大，产生切削热增多，切削温度升高。

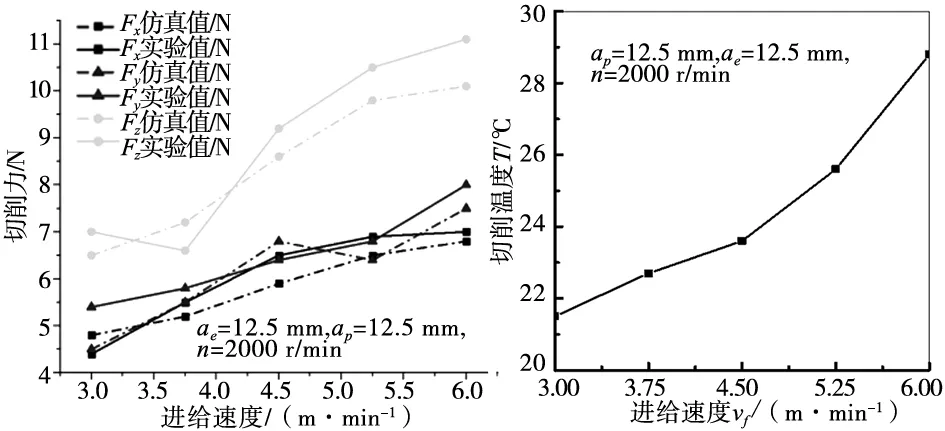
图11 三向切削力随进给 速度的变化曲线 图12 切削温度随进给 速度的变化曲线

4.4 主轴转速对切削力热的影响

三向切削力随着主轴转速的变化如图13所示，随着主轴转速的增加，三向切削力逐渐减小。主要是因为提高主轴转速，刀具沿进给方向切削速度增大，使得圆盘刀只需要更小的切削力便能更容易切断蜂窝材料。三向切削力实验与仿真值最大误差为8.2%、6.5%和7.3%。

分析图14，随着主轴转速的提高，切削温度上升较为明显，这是由于提高主轴转速，刀具沿进给方向切削速度增大，使得刀具前刀面与蜂窝芯接触区域产生切削热迅速增加，温度上升。

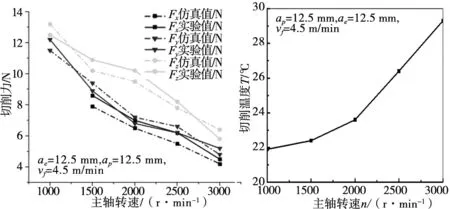
图13 三向切削力随主轴 转速的变化曲线 图14 切削温度随主轴 转速的变化曲线

5 切削热数值模型

对于切削力数值模型方面，袁信满等[10]以中心复合响应曲面法为基础，设计切削试验，已建立圆盘刀超声复合铣削NOMEX蜂窝材料的三方向铣削力预测模型，且模型拟合良好。大多研究往往未将切削热考虑在内，而切削热是导致刀具磨损重要原因，因此本文主要建立切削热数值模型。

切削参数下的温度云图如图15所示，切削过程中，剪切能、摩擦能、表面能等能量除去热辐射大部分都转化为热能，且热量主要集中于锯齿状刀刃与材料接触表面处，温度最大为110.5 ℃，而Nomex蜂窝芯热传导率低，导致整个工件的的温度较低。

图15 切削温度云图

前期单因素实验中，进给速度与主轴转速明显影响较大，因此以圆盘刀进给速度vf、主轴转速n为两个设计变量，切削温度T为响应值，以两因素三水平的中心复合设计方法建立切削仿真加工实验方案，得到13个拟合样本点数据，如表4所示。

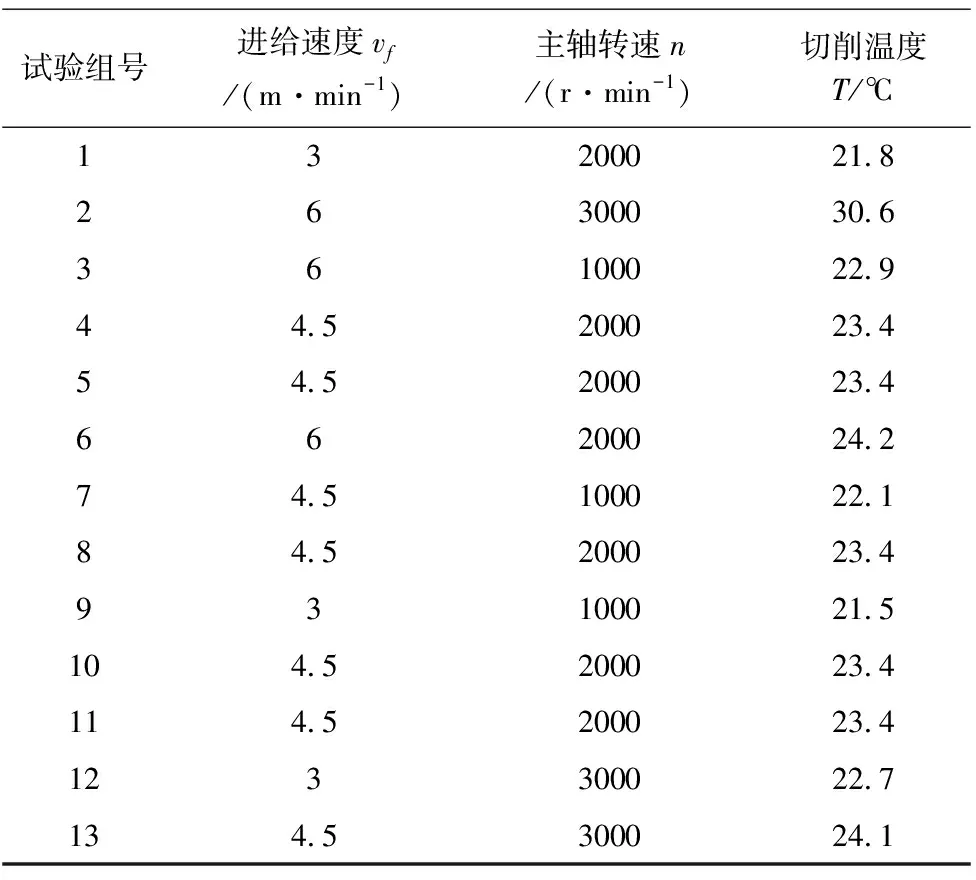
表4 切削温度数值模型拟合样本点

以表4所示拟合样本点数据为基础，采用逐步回归法对圆盘锯齿刀超声振动切削蜂窝芯切削温度数值模型拟合，在不影响方程精度的情况下，得到一次回归模型：

T=+23.874-0.867vf-0.003n+0.001nvf

(2)

如表5所示，切削温度模型方差为0.002，工艺参数显著；失拟项为0.35，模型拟合程度高；R2=0.871 7，调整R2=0.828 9，表明该模型可对82.89%实验数据进行解释，模型拟合良好。

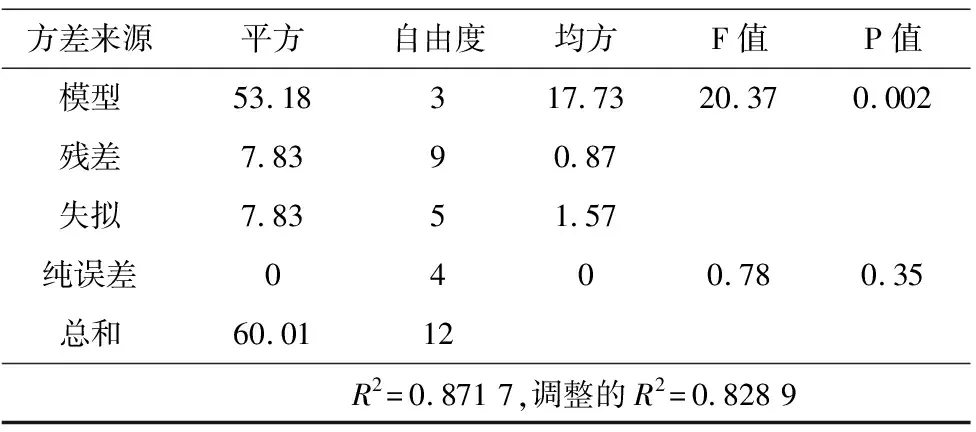
表5 切削温度数值模型方差分析

仿真温度云图中，热量更多的集中于刀刃部分，刀具旋转使得刀刃受到周期性的残余压应力，使刀刃磨损。图16所示为报废后的圆盘锯齿刀，可以看出锯齿状的刀刃部分受损明显，与有限元温度场所分析的温度分布特征一致，验证了模型的有效性。

图16 报废圆盘锯齿刀

6 结论

(1)建立了圆盘锯齿刀超声振动切削Nomex蜂窝芯有限元模型，并建立单因素实验验证，得到仿真与试验对比的切削参数与切削力的变化曲线。切削力仿真值与实验值的最大误差为14.3%，所建立模型有效可靠。

(2)切削参数中，进给速度与主轴转速对切削温度影响显著，以进给速度与主轴转速建立得到圆盘锯齿刀超声振动切削Nomex蜂窝芯切削温度一次回归模型，模型有效可靠，可用于实际预测。

(3)圆盘锯齿刀超声振动切削Nomex蜂窝芯时，为得到更高加工效率并降低切削温度，减小刀具磨损，应采用较大切削深度与切削宽度，较小进给速度和主轴转速。