基于双椭圆滤波算法的傅里叶变换轮廓术*

徐友洪，童根树

(1.衢州职业技术学院信息工程学院，浙江 衢州 324000;2. 浙江大学建筑工程学院，杭州 310058)

0 引言

数控机床作为现代制造业的关键设备，可生产用于航空航天、汽车及医疗保健等方面的复杂零部件，然而由于传统的利用机械探针的测试方法具有测量速度慢、易损伤零件表面及难以适应曲面测量的特点，在线检测和加工过程质量保证技术的发展并不适应加工技术的发展水平，因此就需要一套复杂曲面的三维轮廓测量系统，用于评价成品的加工质量或为数控加工过程提供数据。随着激光技术[1]、生物技术、宽带通信和机器视觉[2]的发展，光学测量技术已经成为非常重要的非接触式3D测量技术。但如何精确获取被测对象的三维轮廓数据信息还是当前面临的一个关键问题。目前，最常用的三维测量技术包括相移轮廓术(PSP)[3]和傅里叶变换轮廓术(Fourier Transform Profilometry, FTP)[4]。相移测量轮廓术(Phase Shift Profilometry, PSP)是一种新的光学三维轮廓测量技术，这种方法结合正弦光栅投影和数字相移等技术，以及高精度的相移装置，且至少采集两幅图像才能获取携带物体高度的信息；而傅里叶变换轮廓术(FTP)仅需一幅光栅图就可以以较高的测量速度及精度获取物体三维轮廓数据。

近几年，FTP技术从原来的一维傅立叶与单频条纹到二维傅立叶变换与双频条纹已被广泛研究[5]。FTP技术提取一阶谱信息将需要一个适当的带通滤波器从频域中将它与背景频谱、高阶谱和噪声等信息分离出来。为消除背景频谱，文献[6]采用小波变换分离的条纹基频信息；文献[7]使用汉宁窗旋转滤波窗使其短轴方向与基频方向一致来获得基频频谱信息等。但是，这些方法[8]都难以完全消除滤波引起的频谱信息泄露问题，如边缘、垂直梯度处和光滑曲面信息等，带通滤波器的发展不具有有效的解决这些问题，从而影响傅里叶变换轮廓术的精度。综述所述，为改善带通滤波器对测量精度的影响，本文提出一种双椭圆带通滤波技术，该滤波技术可以有效地滤除背景和高阶谱分离基频频谱信息。此方法牵涉到的频谱位置及频谱宽度等关键技术问题[9]，本文进行定量讨论，与传统常用的几种滤波器相比较取得更好的实验测量结果。

1 测量原理

1.1 傅里叶变换测量轮廓术(FTP)

傅里叶变换测量轮廓术的光路设计如图1所示，投影系统中心与相机光心的中心距离为d，投射系统中心或成像系统光心到参考面距离l，被测物体高度h(x,y)。CCD获取的畸变光栅条纹为：

g(x,y)=α(x,y)+β(x,y)cos(2πf0x+φ(x,y))

(1)

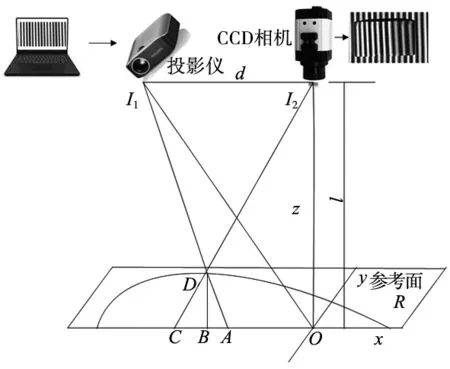
图1 传统相位测量轮廓术的测量系统图

其中，g(x,y)是CCD成像系统接收到的光强值；α(x,y)项表示投射光场中缓慢变化的背景分量；β(x,y)项表示条纹幅度；f0表示投射到参考面的光栅条纹频率；φ(x,y)是表示由被测物体曲面轮廓引起的相位变化值，φ(x,y)=2πf0|AB|；对式(1)进行一维傅里叶变换：

G(f,y)=α(f,y)+C(f-f0,y)+C(f+f0,y)

(2)

频谱如图2所示，由于α(f,y)相对f0变化缓慢，所以在频谱图中与f0是分开的，即图中的背景分量Q0部分，而一阶频谱C(f-f0,y)(Q1)携带物体高度信息。用一恰当滤波器分离一阶频谱分量Q1平移至原点C(f,y)，再进行逆傅里叶，获取相位值如式(3)所示。

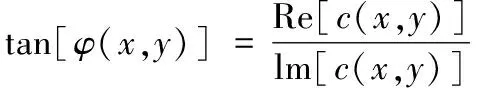
(3)

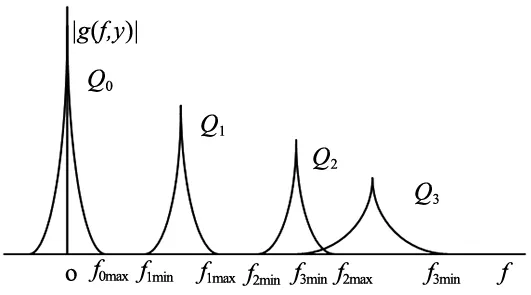
图2 傅里叶变换频谱图

Re[c(x,y)]和lm[c(x,y)]分别表示复数的实部和虚部，φ(x,y)即为物体表面畸变光栅像与参考平面的相差主值，取值[-π,π]，相位经过解包裹(unwrapping)[10]处理可得到连续的相位φ′(x,y)，并由式(4)求得物体的实际高度为：

(4)

1.2 双椭圆滤波器设计

用滤波的方法滤除其高频部分就能去掉噪声[11]，以获取携带高度信息的基频信号沿着x或y轴延伸。现有最常用的4种滤波函数为Bartlett、Blackman-Harris、Hamming和Hanning滤波器，根据文献[12]可知，在一般情况下，一阶频谱实际上是沿x轴和y轴的一个椭圆形状，一般窗函数滤波原理如图3a及图3b所示，可以看出传统带通滤波器不再能够完整提取一阶频谱区域或存在较大冗余数据。由于获得该频谱本质上携带精确的3-D轮廓数据信息，尽可能多地获得该频谱信号，需要更精确分离出携带有物体高度信息，必须尽可能多的分离出一阶频谱信息且避免冗余的频谱数据而产生不需要的测量误差应。因此，为了获得更准确的三维轮廓，本文设计一种双椭圆形窗口滤波器更有效分离出一阶频谱如图4所示。在x方向上，长半轴fa1和短半轴fb1的椭圆形过滤的范围被定义为：

(5)

在y方向上，长半轴fa2和短半轴fb2的椭圆形过滤的范围被定义为：

(6)

其中，fa和fb分别为椭圆滤波x，y方向半径，(fx，fy)为基频信号区域中心处坐标。Q0代表背景频谱，Q1代表携带高度信息的一阶频谱，Q2、Q3及Qn代表高频信号。

(a) 小尺寸窗口

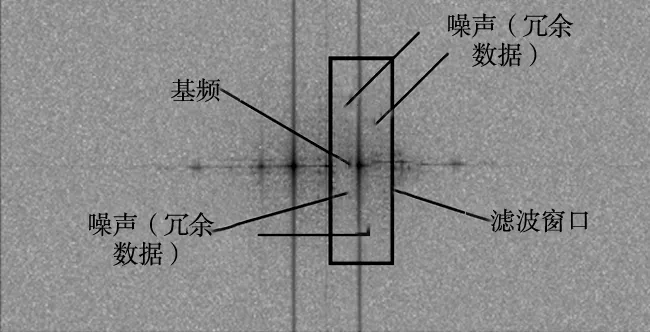
(b) 大尺寸窗口图3 基于傅里叶变换的传统窗函数滤波原理

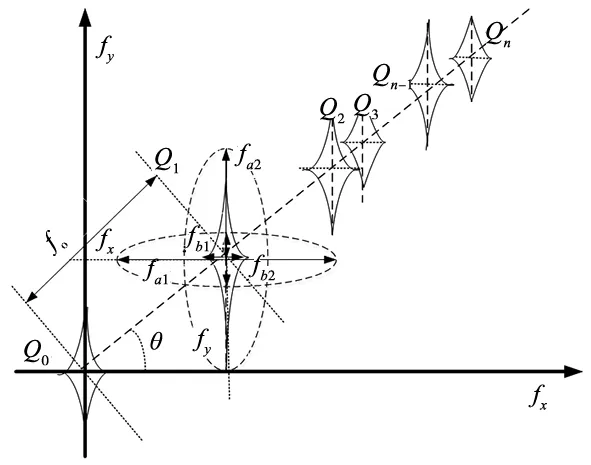
(a) 双椭圆滤波窗口示意图

(b) 双椭圆滤波窗口图4 基于傅里叶变换的双椭圆滤波原理

为获得准确的3-D重建信息，确定函数参数fa1、fb1、fa2和fb2，在不发生频谱混叠的状态下，尽量取大一些为好；在一般情况下，参数取值为一阶谱在整个频谱范围内延伸长度。

在FTP中执行过滤过程以获得频域中的基频，进行傅立叶变换，就通过等式定义的椭圆滤波器对所得光谱进行滤波。基于傅里叶变换的三维重建过程如图5所示，在LabVIEW中，IMAQ通常用于指定图像中的关注区域(ROI)。使用IMAQ手动选择傅立叶频谱中与基频分量相对应的区域。图像显示在外部显示窗口中，通过计算得到最佳的过滤尺寸和位置。

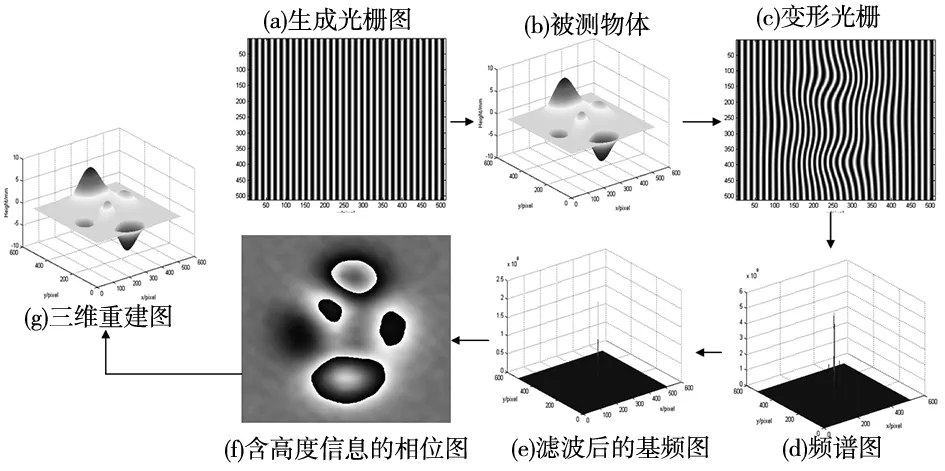
图5 基于傅里叶变换轮廓术的三维重建仿真过程

2 双椭圆带通滤波器适用范围

由于傅里叶变换测量方法使用了傅里叶变换和在频域中的滤波运算，只有频谱中的基频分量对于获取物体高度信息是有效的，但是防止频谱混叠的要求限制傅里叶变换轮廓术的最大可测范围，讨论该技术测量表面梯度的条件，下面给出定量分析。定义高阶谱沿x轴和y轴的局部瞬时空间频率分别为：

(7)

(8)

(f1)max<(fn)min(n>0)

(9)

(f1)min>fbmax

(10)

从图2上看，为防止一阶频谱分量与其它各级频谱混叠，必须满足：

(11)

(12)

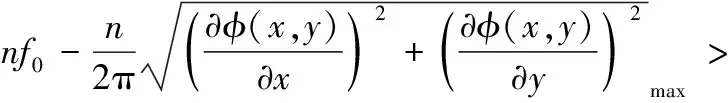
(13)

(14)

(15)

l≫h(x,y)fx=f0cosθ

(16)

(17)

(18)

(19)

进一步简化，得：

(20)

通过式(18)和式(20)，约束条件的曲面重构方面的最大可测梯度可以被定义为：

(21)

此结论说明，傅里叶变换轮廓术最大测量范围受到被测物体高度分布在光栅垂直方向上的变化率的限制，虽然增加l/d也可以增加测量范围，但是这也同时意味着降低了系统灵敏度。因此，在不改变系统参数的前提下，提高测量范围更有意义。

在FTP运算中，只有频谱中的基频分量对获取物体的高度信息是有效的，且频谱混叠限制了FTP的测量范围，由文献可知，基于单频FTP的测量限制条件为：

(22)

式中说明，FTP最大测量范围受到在光栅垂直方向上相位的梯度以及物体高度的梯度限制。很明显，在本文中定义的条件限制的最大梯度比传统单频FTP测量的梯度有所提高。此外，本文所提出的滤波方法在一阶频谱的提取上有明显的优势。分析结果表明，根据物体表面的曲率，投影条纹的倾斜角度可以调整到最大，有利于大表面较大梯度物体的测量，如圆形表面等具有更高的表面梯度物体轮廓三维重建。

3 实验分析

本实验使用的设备为DMK 51BU02 CCD 摄像机和EMP-720液晶投影仪。实验采用的测量光路如图1所示，傅里叶轮廓术分析过程如图6所示，基于双椭圆形滤波器恢复的三维物体重建图及某垂直截面图如图7所示。

(a)被测三维物体模型 (b) 携带物体三维信息的畸变光栅

(c) 双椭圆带通滤波图6 傅里叶变换轮廓术分析

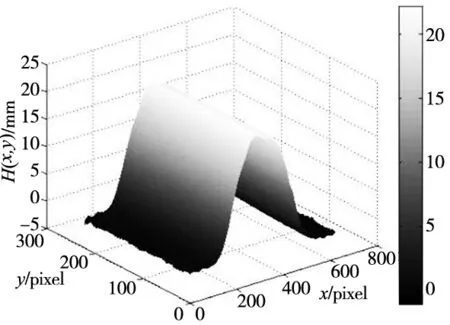
(a) 三维轮廓重建图

(b) 某一位置上的垂直截面图

任意选取被测物体上的6组点云数据，利用目前应用较为广泛的4种窗函数滤波算法和本文提出的椭圆滤波算法的结果作比较，参考点是选取的像素点的位置，实际高度由高精度三坐标测量仪(MGH系列)获取；选取部分数据如表1所示。

表1 传统滤波和椭圆滤波算法的实验数据对比分析

为更精确反应本算法的测量精度，故采用均方根误差(Root Mean Square Error，RMSE)来评判，RMSE定义为：

(23)

式中，Hr(x,y)表示实际高度值；Hm(x,y)表示测量高度值；m表示点云数。采集三维物体20行共500个点云数据，详细分析结果如表2所示，本文所提基于椭圆滤波傅里叶轮廓测量技术的RMSE值总体略小于基于其它滤波窗函数的RMSE值，实验数据表明该滤波方法可行有效，测量精度较高，具有较强的适用性。

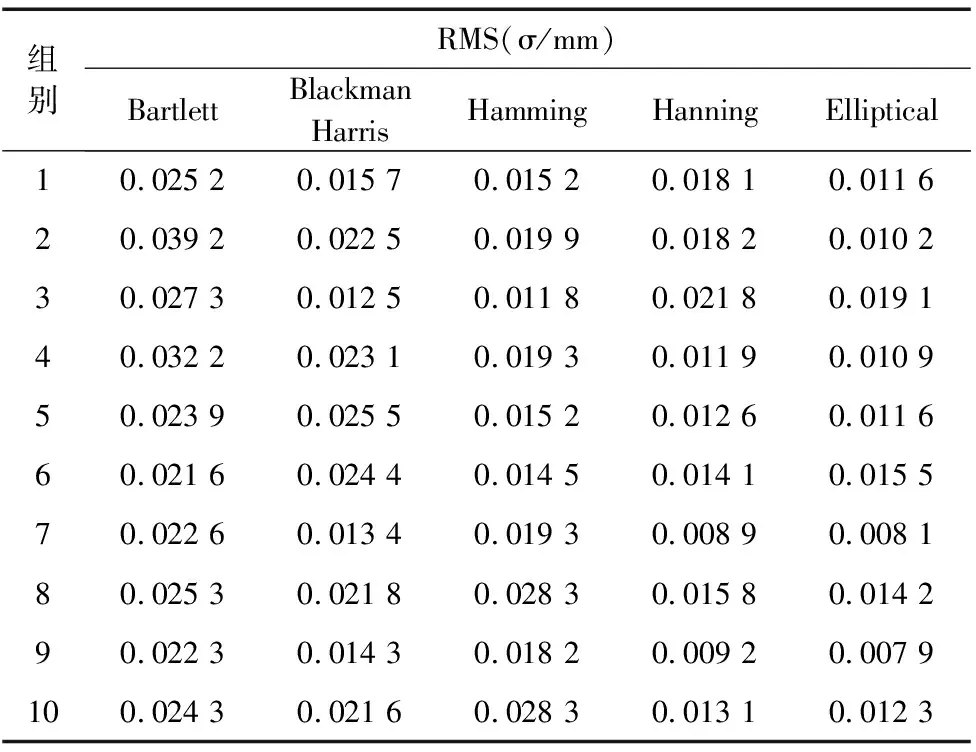
表2 实际值与测量值的均方根误差(RMSE)

4 结论

傅里叶变换轮廓术的测量精度除依赖于高质量的相位去包裹算法外，很大程度上取决于频域滤波算法获取一阶谱的完整性。传统带通滤波很难精确分离一阶频谱，导致3D轮廓恢复精度不高，因此，本文针对频域滤波算法进行比较分析，提出一种基于双椭圆滤波的傅里叶轮廓测量术。实验结果表明，与传统带通滤波算法相比，在测量较大梯度物体轮廓时，本文提出的双椭圆滤波算法的测量精度与可测梯度都优于传统滤波器，具有较高分辨率和噪声鲁棒性的优点。