基于t-SNE和核马氏距离的滚动轴承健康状态评估
胡启国,杜春超,罗 棚
(重庆交通大学机电与车辆工程学院,重庆 400074)
0 引言
滚动轴承是一个被广泛应用于机械设备中的重要元件,其性能的好坏直接影响设备运行的安全可靠性,对滚动轴承进行预测与健康管理(prognostics and health management, PHM)[1]就显得尤为重要。通常,滚动轴承在全寿命周期过程中都要经历一系列不同程度的性能退化状态。对滚动轴承制定有针对性地维护计划,从而有效地避免滚动轴承因故障而失效。基于此思想,一种主动维护技术[2]的滚动轴承健康状态评估方法被提出,与以往的故障诊断相比,更侧重对滚动轴承当前状态描述和退化趋势的分析。
国内外专家学者对滚动轴承的健康状态评估的研究主要基于监测数据。文献[3]利用经验模态分解和奇异值分解提取振动信号的状态特征,然后运用马田系统构造马氏空间,降低状态特征的维度,最后引入健康度的概念,对复杂系统的健康问题进行评估。文献[4]提出了一种混沌优化果蝇算法与多核超球体支持向量机相结合的滚动轴承健康状态定量评估方法。文献[5]利用局部均值分解对滚动轴承振动信号进行分解,并构造特征向量,将其输入支持向量数据描述分类器,进行滚动轴承的健康状态评估。文献[6]采用流行空间主曲线相似度法对高维特征空间进行降维处理并结合离散 Frechet 距离做出轴承健康状态评估。针对大数据高维退化特征集时,很多学者将数据降维方法运用到设备健康状态评估和剩余寿命预测中,既保留有效信息又减低了特征维数,其中常见的降维方法有PCA[7]、ISOMAP[8]、JADE[9]等。文献[10]提出了一种数据驱动对盾构装备刀盘健康评估的方法,采用t-SNE对高维特征集进行低维处理,在优化后的特征空间构造马氏距离度量。性能健康状态评估是基于特征空间内无故障样本与故障样本之间能较好的区分,但是在实际情况中无故障样本不可能存在一个具体的区域,或者故障程度的不同也会存在较大程度重叠。核方法能够很好解决该问题,因为此方法能使低维空间中无法分类的问题在高维空间变得线性可分。因此,有学者将核函数和核马氏距离相结合,得到了核马氏距离[11]。
本文将核马氏距离引入滚动轴承健康状态评估,以滚动轴承全寿命试验数据在多域中对退化状态特征信息进行提取,并利用随机森林算法对退化状态特征信息进行初次筛选,构建高维退化状态特征集,然后利用t-SNE算法进行降维处理,并在核马氏空间中对降维后的退化状态特征进行度量,最后引入健康指数对其进行健康状态评估。
1 特征的提取与选择
1.1 基于多域特征提取
在特征提取过程中,时域、频域或时频域等单域的一个特征或多个特征不能有效准确的呈现滚动轴承性能退化全寿命周期过程,将影响滚动轴承健康状态评估的准确性,而从多域提取故障特征信息可以更加全面准确的反映全寿命周期滚动轴承的性能退化过程。因此,本文从时域、频域以及时频域提取故障特征,具体如表1所示。

表1 各域的特征指标
1.2 基于随机森林法特征选择
随机森林算法[12]是集成学习bagging类方法的一种,在绝大多数数据集上表现出的性能要好于单独的决策树,其本身也可以作为一种特征选择的方法,能够较为准确的评估特征的重要性。
假设数据集有m个样本S={s1,s2,s3,…,sm} 和n个特征F={f1,f2,f3,…,fn},任意一个训练数据样本si,则计算特征fi的重要性,其表达式为:
(1)
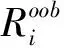
2 轴承性能退化评估方法
2.1 t-SNE流形学习算法
t分布随机近邻嵌入(t-SNE)算法是一种深度学习的非线性流形学习算法[13],是SNE的衍生算法,其主要区别在于t-SNE中的代价函数的使用不同,能够更有效地实现高维数据的可视化降维。t-SNE算法的核心思想是通过将高维空间中的数据点映射到低维空间中,并使得高维数据样本和低维数据样本的概率分布尽可能地不变,从而达到维数约简的目的。其算法的步骤如下:
(1)构建高维数据样本的概率分布
定义集合X={x1,x2,…,xn}⊆RD,假设xi和xj为集合X中的任意两个样本,则高维空间中两个样本的条件概率Pj|i:
(2)
式中,σi表示以xi为中心的高斯分布方差,其可以根据困惑度Perp和二分搜索确定,困惑度的求解如下:
Perp(Pi)=2H(Pi)
(3)
式中,H(Pi)是概率分布Pi的香农信息熵,其定义为:
(4)
(2)计算xi和xj两个样本的联合概率密度函数
(5)
(3)构建低维数据样本的概率分布
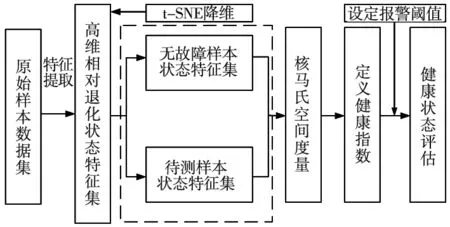
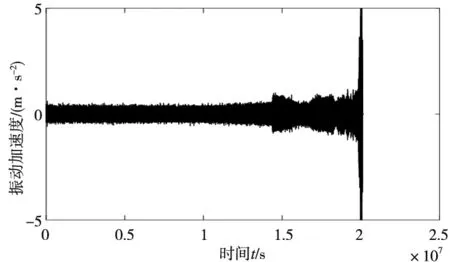
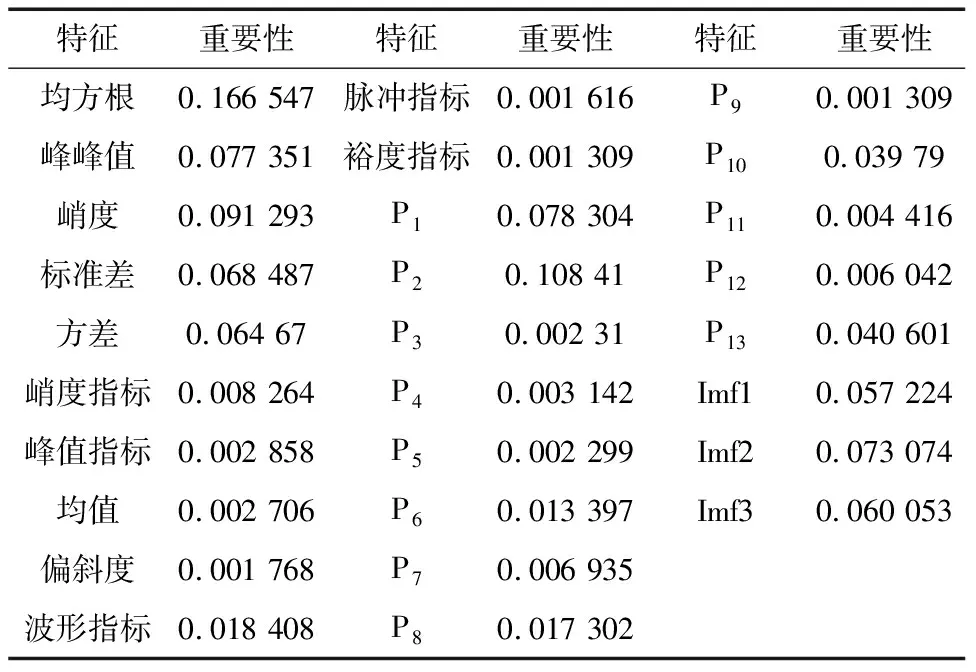
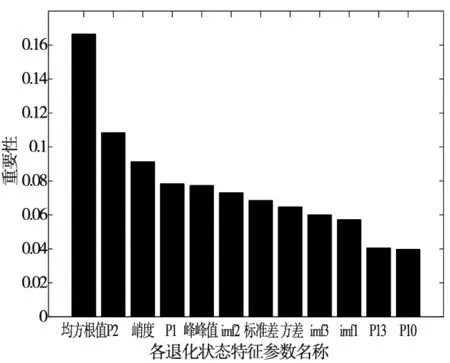
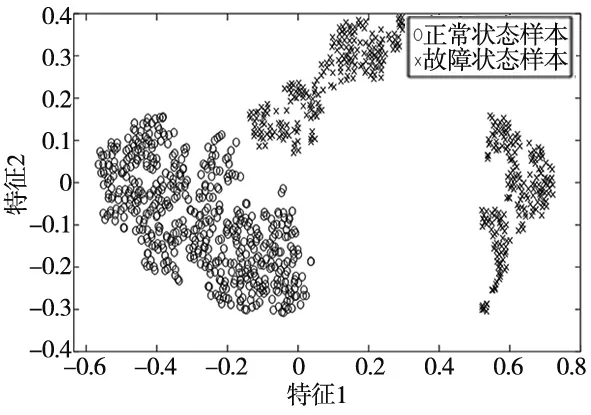
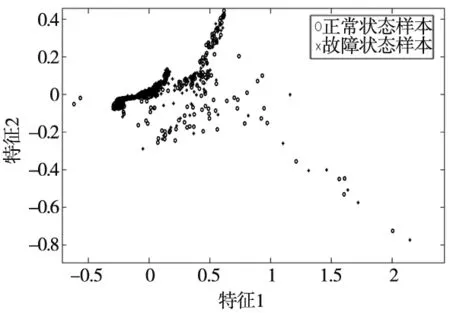
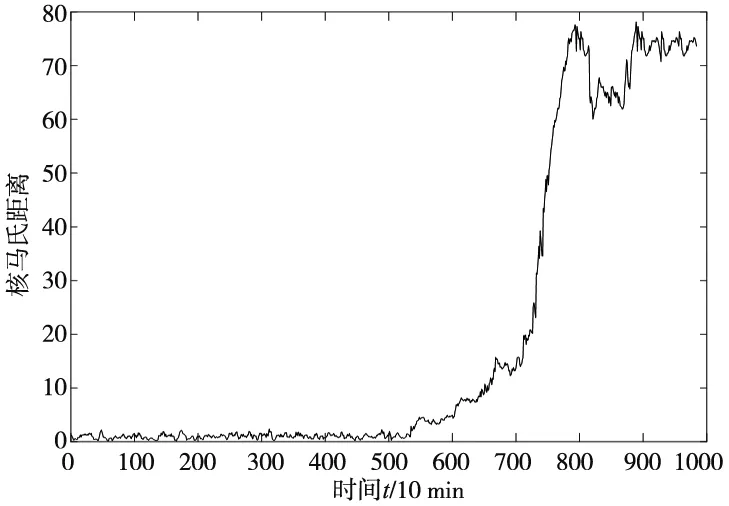
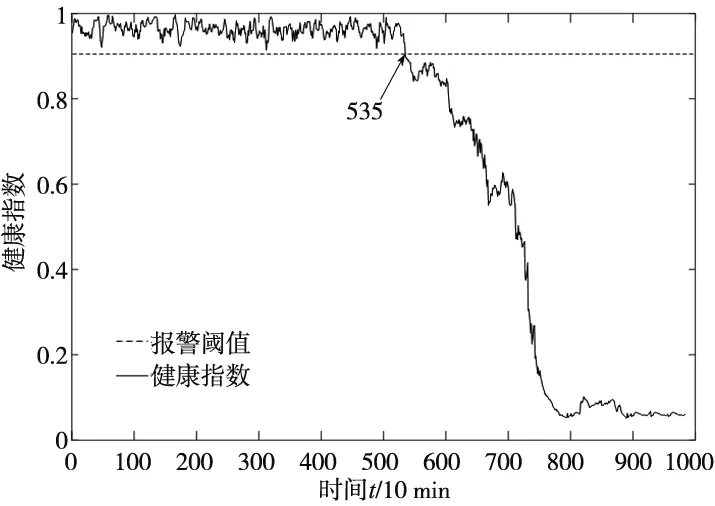
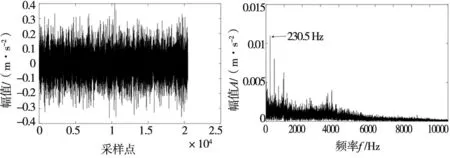
定义Z={z1,z2,…,zn}⊆Rd,且d (6) (7) 式中,C为KL散度,表示高维概率分布与低维概率分布的相似度,其定义为: (8) (5)得到低维数据 (9) 式中,k为迭代次数,α为学习效率,m为动量因子。 (6)迭代循环(3)、(4)、(5),直到迭代次数满足,即可提高低维空间数据的正确性。 多域低维特征向量集与无故障样本数据特征向量集映射到核空间,并计算两者在核空间的偏离程度由核马氏距离表示,此距离越大,表明滚动轴承工作状态偏离无故障状态越严重,处于退化状态或失效状态,相反,滚动轴承处于无故障状态。设映射到核空间F的样本集为φ(x)=[φ(x1),φ(x2),…,φ(xn)]。 核马氏距离可表达为: (10) 式中,φ(xi)为映射到核空间的多域特征向量集,φu为映射到核空间的无故障样本特征集,M为样本集φ(x) 的协方差。 为了更直观的描述滚动轴承的性能状态,引入健康指数来量化滚动轴承的性能状态。其主要思想是使用相应的函数表达式将多域特征向量集的全部信息映射到[0,1]的范围内,若取值接近1,则表示滚动轴承处于健康状态;若取值接近0,则表示滚动轴承处于故障或失效状态。其定义如下: HI=exp(-α·kd2) (11) 式中,α为调节参数,其作用是将健康指数均匀的分布在[0,1]的范围内。 由于健康指数是一个连续变化的指标参数,可以通过设定报警阈值来对滚动轴承的性能状态进行监测,以保证滚动轴承退化到一定程度能够及时维修。利用切比雪夫不等式定理设定报警阈值: (12) 式中,XHI为健康指数,μHI和σHI分别为健康指数的期望和标准差,k为任意正数。 基于t-SNE和核马氏距离的轴承性能退化评估模型流程图如图1所示。 图1 健康状态评估流程图 其具体步骤如下: (1)针对轴承全寿命试验原始样本数据集,在时域、频域和时频域进行退化状态特征的提取; (2)根据随机森林算法特征选择的步骤进行退化状态特征的重要性评定排序,筛选出前n个特征,构建高维退化状态特征集; (3)采用t-SNE流形学习算法对高维退化状态特征进行降维。设定参数困惑度,将高维退化状态特征集带入t-SNE模型中进行降维,得到低维的退化状态特征集; (4)将低维退化状态特征集进行无故障样本与故障样本区分,选取一段无故障特征样本集,并将其与得到的多域低维退化状态特征向量集在核马氏空间进行度量; (5)利用负指数函数对健康指数进行定义,设定调节参数,将核马氏距离代入健康指数的定义式中,并利用切比雪夫不等式计算正常状态样本的健康指数区间范围,设定报警阈值,以此对滚动轴承进行性能退化状态评估。 本文实验数据采用辛辛那提大学公布的滚动轴承全寿命试验数据。试验台的主轴由交流电机通过皮带耦合驱动,其转速为2000 r/min。主轴装有4个Rexnord ZA-2115型号的双列滚柱轴承。试验过程中,每个轴承将承受26 670 N的径向载荷,每个轴承的横向和纵向均安装有一个PCB353B33压电式加速度传感器,用来采集轴承水平和竖直方向的振动信号。数据采集采用NI-DAQ-Card-6062E型采集卡,采样频率为20 kHz,采样间隔为10 min,每次采样20 480个数据点,共采集了984组数据,轴承全寿命原始样本如图2所示。 图2 轴承全寿命原始样本图 针对试验轴承的全寿命周期数据,分别提取时域、频域和时频域的28个退化状态特征参数。为了使退化状态特征集中尽可能地包含有用的信息,需要对有些不能反映轴承退化过程的特征参数进行剔除。首先,对每个退化状态特征进行标准化处理和归一化处理,然后,结合1.2节的基于随机森林特征选择的方法对28个退化状态特征进行选择,各个特征的重要性以及前12位退化状态特征排序如表2和图3所示。 表2 各退化状态特征参数重要性 图3 前12个特征重要性排序图 基于以上的退化状态特征参数选择,最后选取前12个退化状态特征参数构建成高维特征集。 (13) 为了验证t-SNE流形学习算法进行退化状态特征降维方法的有效性与优越性,将其与几种不同非线性降维方法进行对比,其降维后的样本低维特征分布图如图4所示。 (a) t-SNE低维特征分布图 (b) Isomap低维特征分布图 (c) KPCA低维特征分布图图4 不同方法低维特征分布图 从图4a可以看出,基于t-SNE算法的降维方法对正常状态样本与故障状态样本进行了有效的区分,没有出现混叠现象。图4b中Isomap降维方法基本能够保持全局特征,但是在性能衰退初期阶段,还是会存在混叠现象。图4c中KPCA降维方法虽然能够表征一定的退化趋势,但是正常状态样本和故障状态样本明显出现了混叠交叉,且数据样本较为分散。由此分析,可证明t-SNE方法在高维退化状态特征集中降维的有效性和优越性。 采用t-SNE对高维退化状态特征向量集进行降维,设置嵌入维数d=2,得到低维特征向量集。针对降维处理后的退化状态特征集,将第100个样本到第400个样本作为无故障特征样本。计算待测样本与无故障样本在核马氏空间中的距离,经过平滑处理后的结果如图5所示。 图5 核马氏空间度量 可以看出,滚动轴承在全寿命试验的无故障时期,在核马氏空间中的待测样本,其距离波动较小,而当滚动轴承进入退化阶段时,其距离波动较大,并且随着轴承故障程度的加深,其值也在不断的增大,符合轴承的衰退过程。将其与原始信号进行比较,核马氏距离能很好的表征了轴承的全寿命衰退过程。 结合t-SNE和核马氏距离度量,引入负指数函数作为轴承健康状态的评价函数,将其值作为健康指数,用于定量刻画轴承健康状态。由于评价函数的衰减敏感度随核马氏距离的增大而减弱,可通过调节式(11)中的参数α来提高其衰减度。因此,取α=0.038 得到健康指数曲线,并通过计算健康指数的期望和标准差,求得其报警阈值φ=0.904 6,如图6所示。 图6 健康指数曲线 可以看出,轴承全寿命过程可以分为4个阶段:0~5350 min处于平稳运行期,即平稳状态;5350~7000 min处于早期故障阶段,即轻度退化状态;7000~9000 min处于中度故障阶段,即中度退化状态;9000 min之后处于严重故障阶段,即失效状态。当轴承全寿命试验进行到第5350 min的时候,其健康指数为0.899 6,而设定的报警阈值为0.904 6,说明轴承在5350 min的时候已经开始退化。 取5350 min的原始样本数据进一步做包络谱分析,原始样本信号见图7a,时域信号进行包络解调得到包络谱见图7b。通过查阅试验轴承的参数,实际的外圈故障频率与包络谱中的230.5 Hz很接近,再次证明轴承在5350 min时已经出现了外圈故障。 (a)原始信号时域图 (b) 包络谱 综上分析,基于t-SNE和核马氏距离的滚动轴承性能退化评估方法,能够对滚动滚轴承不同退化状态进行准确评估,且对早期退化时期的故障具有一定的敏感性,同时也验证了该性能评估方法的有效性。 (1)针对滚动轴承在健康状态评估过程中退化状态特征筛选和健康指数难以构建等问题,本文将t-SNE和核马氏距离相结合,提出了基于t-SNE和核马氏距离的性能健康状态评估方法。采用多域特征更能表征轴承性能退化过程的退化状态特征。 (2)高维退化状态特征集在状态评估中不能充分利用有效值,因此采用t-SNE流形学习进行降维,在核马氏空间对其进行度量得到性能退化曲线,并通过引入健康指数、报警阈值进行健康状态评估。 (3)利用Isomap、KPCA和t-SNE对高维退化特征集进行降维,并对比三种方法得出,t-SNE能够将正常状态样本与故障状态样本有效的分离,不存在交叉混叠现象,降维的效果明显优于其它两种方法。 (4)对全寿命试验数据的验证与分析,证明了所提方法能够有效地评估轴承的性能退化状态,并对轴承早期性能退化状态评估具有一定的优势。2.2 核马氏距离
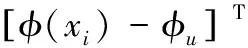
2.3 健康指数
2.4 滚动轴承性能退化评估方法
3 试验与分析
3.1 试验平台和数据
3.2 高维退化状态特征集的构建
3.3 滚动轴承的性能退化评估分析

3.4 滚动轴承的故障验证分析
4 结论

