基于RBF神经网络和扰动观测器的PMLSM位置控制*

张 博，周 达，蒋波涛

(西安工程大学电子信息学院，西安 710600)

0 引言

永磁直线同步电机(Permanent Magnet Linear Synchronous Motor，PMLSM)直接将电能转换成直线运动，其结构简单、响应速度快，已被广泛应用在自动化生产线，民航运输，军事等领域[1-2]。然而，由于采用PMLSM直接驱动的系统，少了机械减速器和传动装置，使得控制系统的柔性变差[3]。此外，PMLSM驱动的控制系统易受系统参数变化、运动摩擦等不确定性因素的影响，造成系统控制性能变差，而其中的负载扰动和模型误差对系统的影响尤为突出[4]。为了解决负载扰动和模型误差影响，本文对提高PMLSM位置控制系统的伺服性能进行研究。

为了提高系统位置跟踪精度以及减少抖振，国内外学者提出了不同的控制方法。高为炳提出的滑模趋近律控制可以改善系统的动态品质并降低系统的抖振。文献[5]中提出了双幂次滑模趋近律和超螺旋扰动观测器相结合的控制策略，通过变边界层的趋近律方法提高系统的控制精度，并通过调节超螺旋滑动观测器的幂指数加快了算法的收敛速度。但超螺旋滑模观测算法的工程应用较为困难。文献[6]将变指数项引入到双幂次滑模趋近律中，改变了双幂次趋近律的趋近速度，但是引入变指数项使得控制器的参数变多，增加了系统的复杂性。文献[7]通过设计滑模趋近律控制器，以提高PMLSM控制性能。然而负载扰动等不确定因素对控制性能的影响未考虑。文献[8]提出了一种改进指数滑模趋近律控制方法，虽然可以提高系统的响应速度，减少抖振但是系统的鲁棒性能没有得到改善。

为了提高PMLSM位置伺服控制的精度, 本文在文献[9]的基础上提出了新型滑模趋近律控制算法，并针对伺服系统中模型误差和负载扰动，设计自适应RBF神经网络逼近器和非线性扰动观测器。本文提出的控制策略能减少系统的抖振，控制精度得到提高、鲁棒性得到改善。通过仿真实验，对所提出的控制方法进行验证。

1 PMLSM系统的数学模型

PMLSM驱动系统是一种非线性、强耦合系统，为了简化，采用id=0的磁场定向控制，对三相PMLSM驱动系统，其电磁推力方程为[10]：

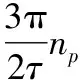
(1)

式中，Fe是电磁推力；kf表示推力系数；iq是q轴的电流；τ为永磁体极距；np为电机的极对数；ψf为永磁体磁链。

而PMLSM运动方程为：

(2)

式中，M为电机的质量；B为粘性摩擦系数；v为动子的运动速度；Fd为系统的模型误差、摩擦力和负载扰动等不确定性的总和。

忽略系统摩擦和参数变化等的影响，PMLSM系统的运动方程为：

(3)

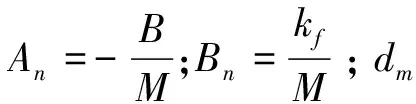
对dm与ds做如下的一些假设:

①建模的不确定ds有界即：|dm|≤D1；D1是有界正常数。

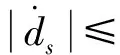
定义状态变量：

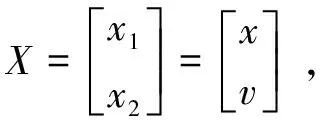
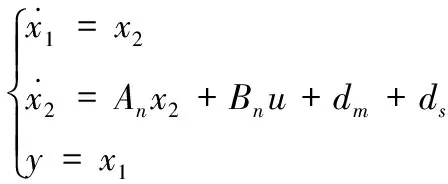
(4)

式中，u为控制器的控制率：u=iq；y为系统的输出变量。

2 控制系统

2.1 控制器的设计

本文设计新型滑模趋近律方程如式(5)所示：

(5)

其中，H(s)=ζ+(1-ξ)e-a|s|

取ζ=0.4；a=200时，H(s)如图1所示。

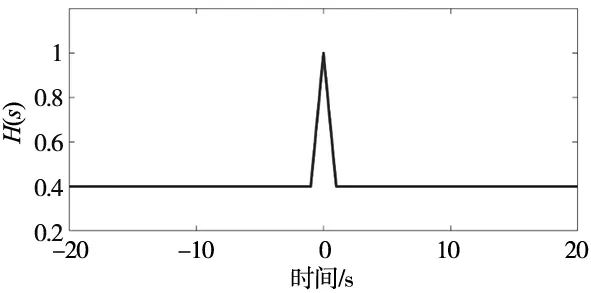
图1 H(s)的函数描述

从图中可以看出当s→0时，H(s)→1；当s→∞时，H(s)→ζ。

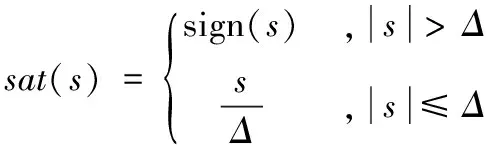
式中，k1>0;k2>0;0<α<1;β>1; 0<ζ<1;a>0;Δ为边界层。

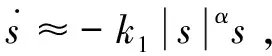
选取滑模面函数为：

(6)

其中,c>0。

设位置追踪误差为：

e=xd-x1

(7)

式中，xd是位置的给定信号。

对式(6)两边求导，并将式(4)、式(5)和式(7)代入，可得控制率u为：

(8)

为了提高控制的精度，本文分别采用RBFNN逼近器估计dm和非线性扰动观测器来估计ds。

2.2 自适应RBF神经网络的设计

RBFNN有着逼近非线性函数的优点，在非线性系统应用广泛[11]。RBFNN由输入层，隐含层和输出层组成，其结构如图2所示。

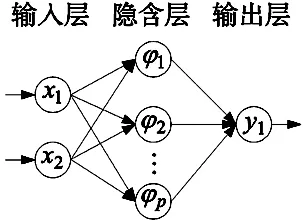
图2 RBFNN的原理框架

RBF神经网络输出结果是：

y(x)=WΤφ(x)+ε

(9)

式中，WΤ是连接隐含层和输出层的权重矩阵；φ(x)是隐含层的非线性函数；ε是神经网络的逼近误差，假设有界,即ε≤ε*，其中ε*是正常数。φ(x)选择高斯函数如下所示：

(10)

式中，bj和cj分别是高斯函数的宽度和中心。

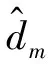
(11)

RBFNN的自适应律按照式(12)，设计为：

(12)

2.3 非线性扰动观测器的设计

非线性扰动观测器设计为[12]：

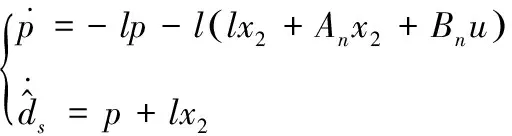
(13)

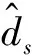
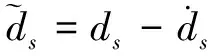
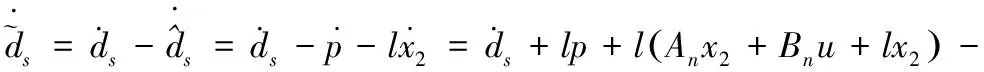
(14)

对式(14)求解微分方程得：

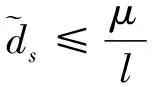
基于自适应RBF神经网络逼近器和非线性扰动观测器，公式(8)控制律改写为：

(15)

由此，本文所提出的PMLSM伺服系统控制策略原理框图如图3所示。

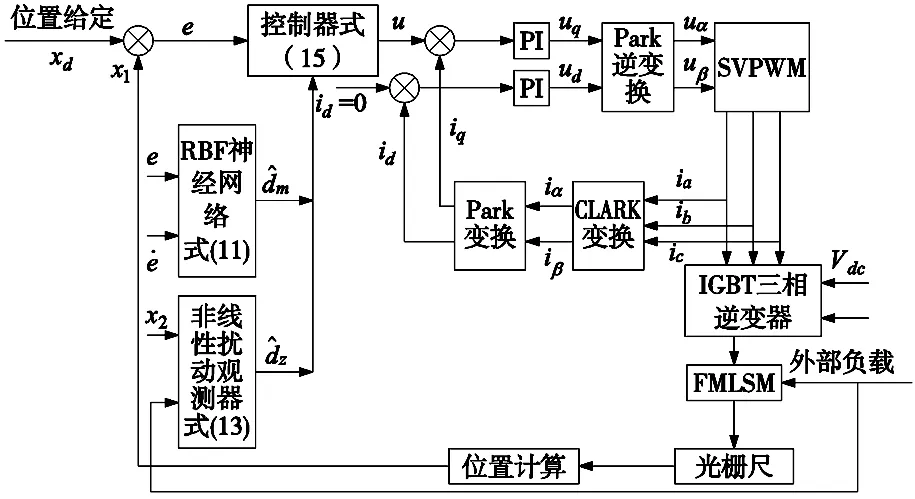
图3 PMLSM伺服系统控制策略原理框图

2.4 系统稳定性证明

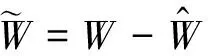
构建Lyapunov函数为:

(16)

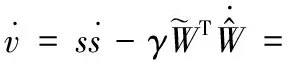
(17)

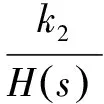
3 仿真结果及分析

为了验证所提的控制策略的有效性，本文对PMLSM驱动的位置控制系统，设计了仿真对比实验，PMLSM的参数如表1所示。

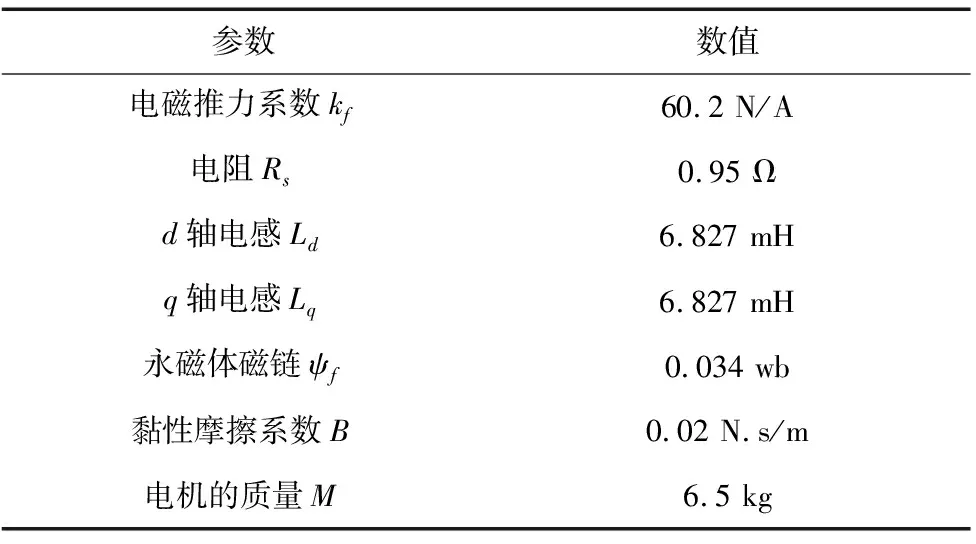
表1 电机参数表

控制器参数为：k1=50；k2=40；c=15;α=0.5;β=1.2;ζ=0.4;γ=0.015;ci=[-1-0.5 0 0.5 1];bi=5；a=200;ε=5；k=30。

本文将建模误差dm表述为：

dm=0.01Bnu+0.01Anx2

位置跟踪信号如图4a所示：

xd=1.2sin(2πt) mm

负载扰动如图4b所示：

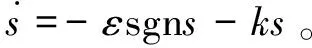
则滑模指数趋近律的控制律u传统为：

(18)

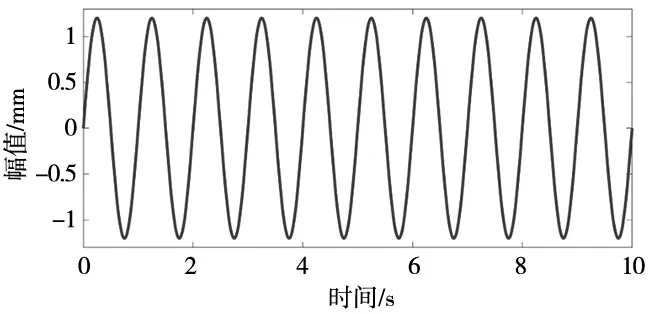
(a)位置跟踪信号

(b)PMLSM系统受到的负载扰动

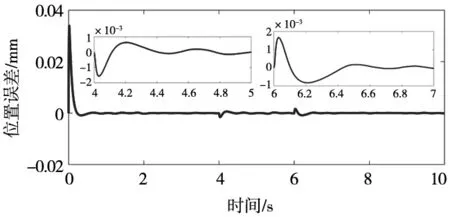
(c)本文所得的位置误差曲线

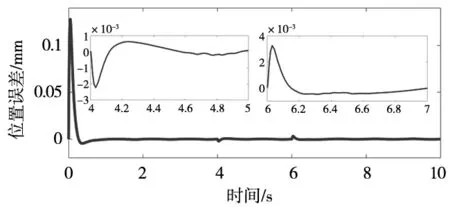
(d)基于传统滑模趋近律的位置误差曲线

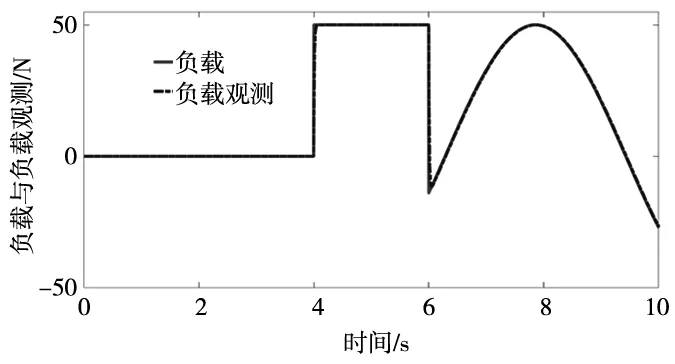
(e)负载扰动观测器所得的仿真结果

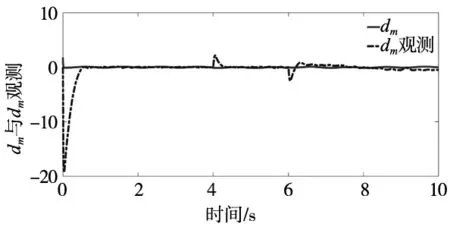
(f)建模误差逼近器所得的仿真曲线

基于本文控制器和传统滑模趋近律的控制方法误差曲线如图4c和图4d所示。在突加负载扰动时，图4c中误差突然增加到1.3 μm和1.5 μm,而图4d中误差突然增加到2.3 μm和3.5 μm。说明本文提出的控制方法具有更高的跟踪精度，位置误差小。图4d可以看出本文提出的非线性扰动观测器能够很好的跟踪负载的变化，系统的鲁棒性能强。图4f在4 s之前施加常数负载扰动，建模误差在5%左右，在6 s后施加一个正弦信号的负载扰动，误差在8%左右。采用本文设计的自适应RBF神经网络逼近器可以很好地逼近所给定的建模误差。

4 结论

针对具有建模误差和负载扰动的永磁直线同步电机伺服控制系统，本文提出了一种结合自适应RBF神经网络逼近器和非线性扰动观测器的滑模趋近律的控制策略。滑模趋近律可以提高系统的动态响应速度，减弱滑模抖振。通过RBF神经网络逼近器和非线性扰动观测器，用以对系统的建模误差进行逼近并对负载扰动进行估计。通过仿真实验，与传统的滑模算法相比，本文所提出的控制策略，位置跟踪精度高，鲁棒性强。