基于组合赋权的TOPSIS模型在刀具优选中的应用*
韩文东,李 晶
(西安工程大学机电工程学院,西安 710048)
0 引言
随着我国制造业以及科学技术的高发展,对机械加工的产品要求也随之提高。过去一些难以加工的金属材料现在的应用也在日益增长,同时大量的复合材料也在不断的研制和应用。正确合理的选择一把刀具,是提高生产率、降低成本和减少环境污染等问题的关键所在。因此刀具优选的目的在于综合考虑影响因素,从有限的侯选刀具中选出相对最优刀具。
刘亮辉等[1]将TOPSIS法与层次分析法结合,首先用层次分析法对各影响因素进行权重确定,再应用TOPSIS法来评价刀具选择模型,进而实现刀具材料的选择。徐坚等[2]以刀具质量、成本和效率建立刀具选择模型,利用模糊层次分析法对所建模型求解得出备选刀具的权重,来实现刀具的优选。李崇洋等[3]将车削用量的优化问题转化为博弈决策问题,并将优化目标的数学模型转化为非合作的博弈决策模型,通过求解得到模型的纳什均衡策略,即更优的车削用量解。王明海等[4]以加工时间、成本、资源消耗、环境影响及加工质量构建两级结构的刀具优选模型,并基于三角模糊数将模糊层次分析法和灰色关联分析进行结合,得到优化后的算法,并以实例证明该方法的有效性及可行性。
目前,上述一些方法已经应用到了实际生产中了,但是大多数情况下还是依据工人或专家的经验及查询相关刀具手册来选取切削刀具,这会将主观因素的影响放大,使得选择的刀具说服力不足。因此,本文提出将AHP(主观赋权)与熵权法(客观赋权)以博弈论思想进行组合,并建立基于博弈论组合赋权的TOPSIS刀具选择模型,来选取满足切削要求的最优刀具。
1 基于博弈论的组合赋权
1.1 熵权法确定客观权重
熵权法是一种不受人为主观因素影响的客观赋权法,它是以各项指标所提供的贡献值为基础来确定评价指标的权重。其基本思想是以客观的评价指标数据为依据,假如评价指标的差异越大,则该评价指标的熵值越小,熵权越大[5]。熵权法赋权具体过程如下[6]:在进行赋权时,先要求解出评价指标的熵值,如式(1)。
(1)
式中,ej为评价指标j的熵值;k为评价指标个数有关的常数;Yij为标准化后的指标值。
接着根据公式(2)求出各项评价指标的熵权。
(2)
因此得到各项评价指标的权重为λ=(λ1,λ2,…λn)。
1.2 AHP法确定主观权
层次分析法是一种层次权重决策分析方法,广泛的应用在处理综合因素问题上,利用专家或专业人士以基本专业原则为前提下根据主观经验来对评价指标进行两两比较形成判断矩阵,并且通过一致性验证后来进行各评价指标的赋权[7-9]。在使用1~9标度的层次分析法对多评价指标进行处理时存在计算量过大、判断错误等问题。因此国内外学者提出了3标度法,3标度法成功的解决掉了工作量过大、判断错误等问题,但是3标度法又将许多评价指标信息丢失、掩盖导致评价误差的增大。为解决这些问题,本文提出1~5标度法既减少判断错误的出现又最大限度的保留评价指标的信息集。其具体过程为:
(1)根据评价指标建立模糊关联矩阵。将刀具选择评价指标N1,N2,N3,…,Nm,两两进行比较,并应用隶属度信息表1对指标定量描述,得到判断矩阵如下:
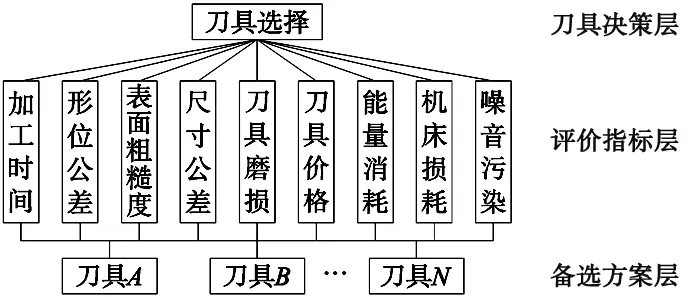
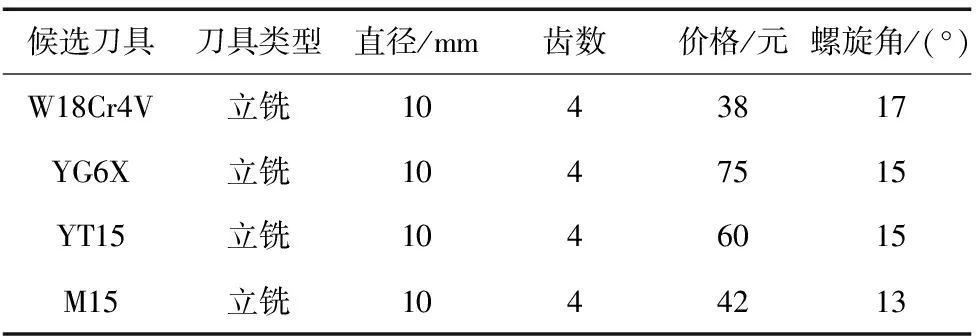
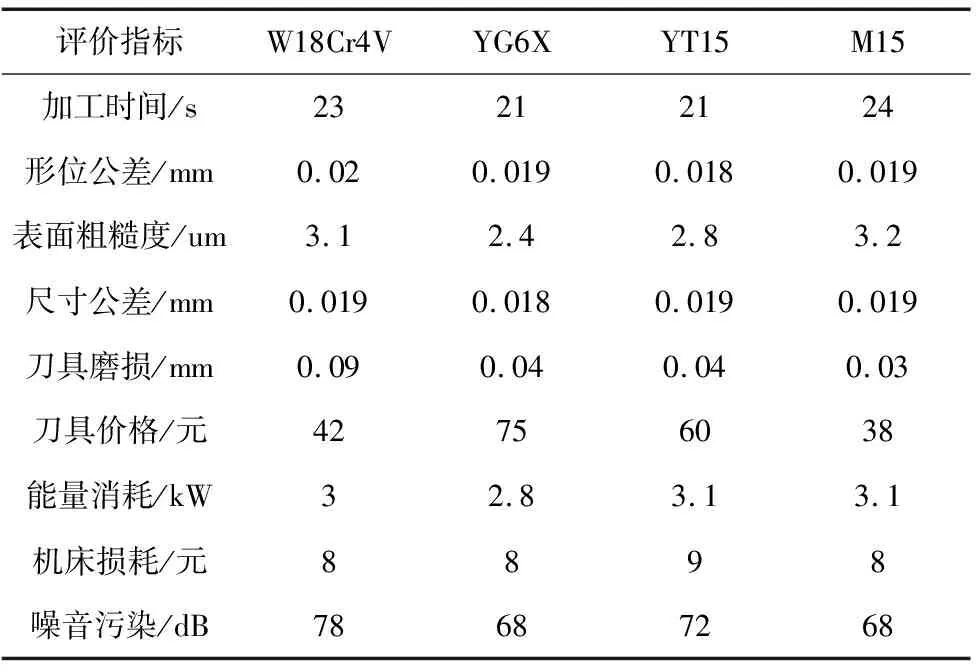
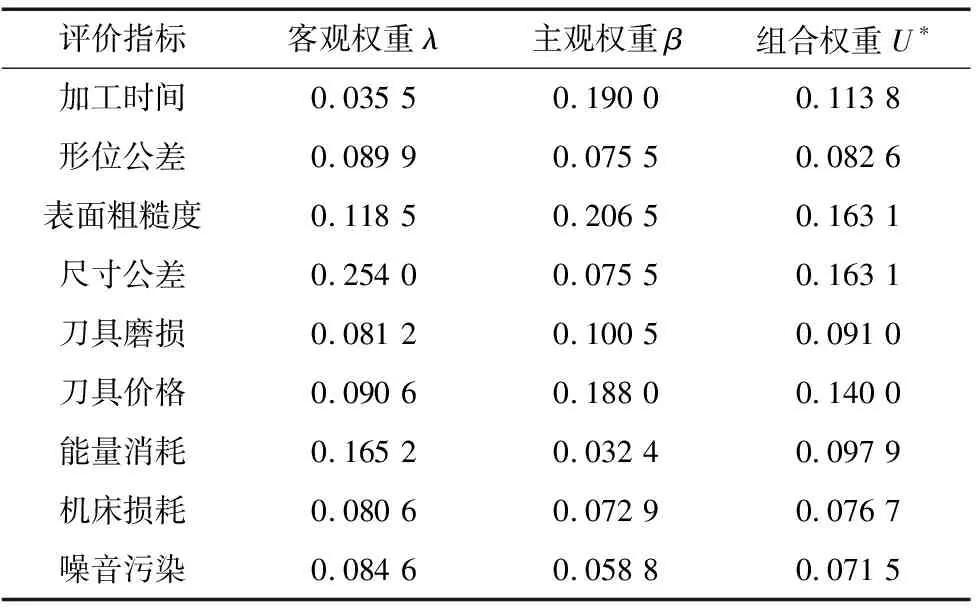
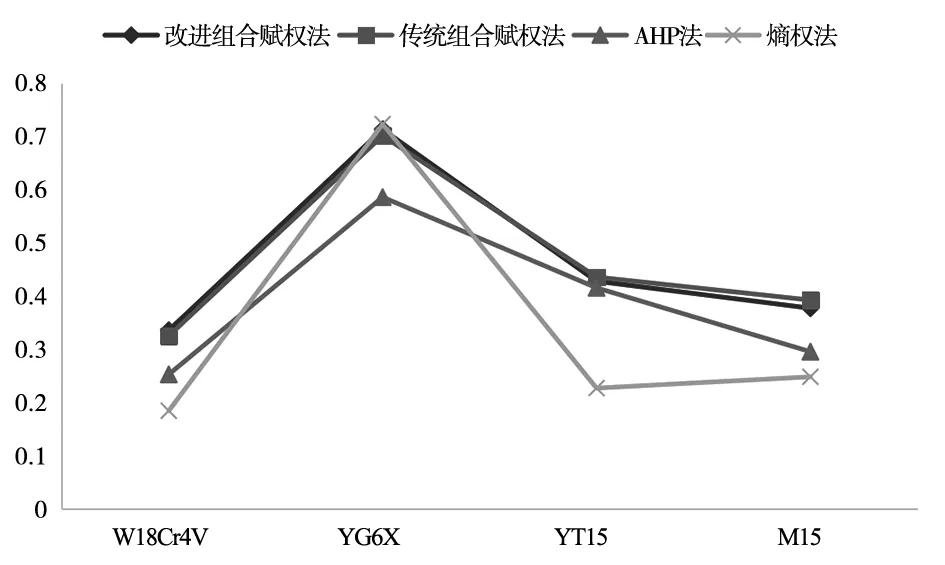
其中,aij是评价指标Ni和Nj依照隶属度信息表比较所得结果,并且由表1可知aij的取值范围满足0 表1 隶属度信息 (2)判断矩阵的一致性检验。构建的判断矩阵A可能存在误差和不一致,因此用一致性检验公式(3)进行检验,当CR<0.1时,矩阵A可以接受;CR≥0.1时,矩阵A不被接受。 (3) 其中,λmax为矩阵A的最大特征值,CI为一致性指标,RI为规定的一致性指标如表2所示。 表2 一致性指标RI查询表 (3)主观赋权。在一致性检验通过后,采用公式(4)计算每个评价指标的主观赋权β=(β1,β2,β3,…,βn)。 (4) 基于博弈论的组合赋权法是以纳什均衡为理论基础的协调方法,就是将主观赋权法及客观赋权法之间的权重冲突以纳什均衡理论为协调手段进行协调,使得各评价指标的权重达到一致和妥协[10]。这种方法可以使主、客观权重达到均衡,考虑到各个评价指标的固有信息,降低主观影响进而提升评价指标的合理性。基于博弈论的组合赋权基本步骤如下[11-12]: (1)首先采用AHP主观赋权法和熵权法客观赋权法依次计算各个评价指标的权重,其权重向量集为Uk={Uk1,Uk2,Uk3,…,Ukn},k=1,2,…,L;其中L为确定权重的方法个数,n为评价指标的个数。假设线性组合权重系数为α={α1,α2,α3,…,αL},则其任意向量的组合为: (5) 其中,αk>0,k=1,2,…,L。 (2)为了达到不同权重间的一致和妥协,需用U和Uk两者的离差极小化为目的,对线性组合权重系数αk进行优化,得到最优的权重,其优化目标函数为: (6) (7) 在实际生产中,会有多种适合生产加工零件的刀具,这些刀具都能满足零件生产的要求。但是在生产加工中普遍要求加工质量高、加工效率高、资源消耗低等因素要求。因此在多种符合零件加工要求的刀具中选择出一把最优刀具就显得十分重要。本文选择加工时间、表面粗糙度、刀具价格等刀具属性建立评价指标集,进而建立刀具评价选择模型。如图1所示。 图1 刀具评价选择模型 TOPSIS法在1981年首次被提出,它是根据有限的评价指标和理想化目标的接近程度进行排序的方法,同时TOPSIS法又称为优劣解距离法[13]。将组合赋权得到的权重系数与初始决策矩阵组合后得到加权决策矩阵,评价指标的权重会影响原有决策矩阵含有的信息和精确度。为了更好的保留决策矩阵的信息集和提高备选方案的数值精度,提出将组合权重与评价指标的理想距离进行组合。建立TOPSIS刀具优选的模型,具体步骤如下: 假设有m个备选刀具,则刀具集M=(M1,M2,M3,…,Mm);评价指标共有n个,则指标集N=(N1,N2,N3,…,Nn)。第Mi个刀具在第Nj的评价指标下的决策值为Cij,则其构建的初始决策矩阵为: (2)初始决策矩阵标准化 因为初始决策矩阵中每一个评价指标的单位、量纲和数量级是存在差别的,所以要对其进行标准化处理。首先利用公式(8)对初始决策矩阵进行指标正向化处理,接着按照公式(9)对初始决策矩阵进行标准化。 xij=cimax-cij (8) (9) 其中,cjmax为同一评价指标的最大值,xij是正向化处理后的指标值。 进过标准化处理的标准化决策矩阵R为: (3)确定“正理想解”和“负理想解” 试验组的包装质量、消毒质量、收回及时度、供给及时度等护理质量评分与对照组进行比较,对照组均低于试验组,差异有统计学意义(P<0.05)。见表1。 “正理想解”和“负理想解”是某一评价指标的最优值和最差值,即: (10) (11) 其中,i=1,2,…,m;j=1,2,…,n。 (4)计算各评价指标的加权理想距离 将组合权重系数与各评价指标进行结合计算各个评价指标到“正理想解”和“负理想解”的距离。其具体组合方法如下: (12) (13) (5)计算相对贴近度εi (14) 由此可知,当εi取到最大值时,即是最合适的加工刀具。 以某机械制造企业采用加工中心来加工材料为铸铁的零件为例,来验证基于博弈论的TOPSIS模型在刀具优选时的可行性和有效性。零件的具体加工要求为:零件进行铣削,零件长为150 mm,宽为120 mm,表面粗糙度为3.2 μm。现在有4种候选铣刀,其主要参数如表2所示。4种候选刀具的评价指标的检测结果,如表3所示。 表3 候选刀具主要参数 表4 候选刀具的评价指标检测结果 通过对候选刀具评价指标检测结果进行整理,可以得到候选刀具的初始决策矩阵。但是初始决策矩阵中的指标单位、量纲存在差别,所以用式(8)和式(9)进行无量纲的标准化处理,得到标准化决策矩阵R。 根据候选刀具的检测数据,利用熵权法计算出评价指标的客观权重λ,根据专家建议和评价结果得到判断矩阵A,用公式(3)进行判断矩阵一致性验证得CR=0.039 4,因此该判断矩阵满足一致性检验。接着用公式(4)计算得到主观权重β。 接着应用式(5)~式(7)将主观赋权法及客观赋权法之间的权重冲突以纳什均衡理论为协调手段进行协调,计算得到权重系数α1=0.543 3,α2=0.690 4,和每个评价指标相对应的组合权重U*,具体值如表3所示。 表5 各评价指标的权重值 根据式(12)、式(13)将组合权重系数与各评价指标进行结合计算各个评价指标到“正理想解”和“负理想解”的距离: 最后依据式(14)计算出每把理想候选刀具的理想贴近度: ε1=0.335 8,ε2=0.712 6 ,ε3=0.427 9 ,ε4=0.377 2 图2 不同评价法的结果对比 由图2可知传统组合赋权法评价结果为YG6X>YT15>M15>W18Cr4V;AHP赋权法评价结果为YG6X>YT15>M15>W18Cr4V;熵权法评价结果为YG6X>M15 >YT15>W18Cr4V。改进组合赋权法刀具的优选是YG6X>YT15>M15>W18Cr4V。 将改进组合赋权法评价结果与传统组合赋权法、AHP赋权法、熵权法进行对比,很明显改进后的组合赋权法计算的数值更加精确、评价指标信息也相对的更加完整。 通过对比可知4种综合评价方法得到的评价顺序基本一致吻合,验证了改进组合赋权法的正确性和有效性。同时也得出了经过综合评价立铣刀具YG6X的综合得分最高,即最优备选方案。 (1)本文提出用1~5标度来改进AHP法,改善了传统AHP法存在的缺陷;将组合权重与理想距离进行结合,改进TOPSIS模型,进而提高综合评价结果的精确度。 (2)将熵权法和改进的AHP法基于博弈论进行结合,应用于TOPSIS模型,建立刀具选择综合评价模型。通过与其它3种赋权评价法的结果进行对比,其对比结果表明了本模型的正确性。 (3)本模型应用于4种备选刀具的综合评价,得到4种备选刀具的综合评价结果符合实际情况,进而验证了本模型的有效性,并为生产加工提供了合理参考。

1.3 基于博弈论的组合赋权
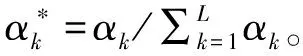
2 TOPSIS刀具评价选择模型
3 实例分析


4 结论

