信息不对称下个人健康数据交易双边定价策略研究
郭鑫鑫 王海燕* 孔 楠
(1.东南大学 经济管理学院,江苏 南京 211189;2.普渡大学 工程学院,印第安纳州 西拉法叶 47906)
0 引言
近年来,在国家政策积极推动及地方政府和产业界的带动下,各类数据交易平台纷纷开始建立,如贵阳大数据交易所、东湖大数据交易中心和华东江苏大数据交易平台等政府类数据交易平台,同时还有京东万象、天元数据、数粮和数据宝等企业类数据交易平台,这标志着我国大数据交易已进入市场化发展阶段[1]。数据交易平台通过对原始数据进行脱敏、清洗等加工处理,然后以数据包和API(应用程序接口)等形式进行交易,同时还提供相关的数据应用服务。伴随着大数据产业的快速发展,数据需求也越发呈现多样化和个性化。为了更好地满足各类数据需求者的需求,数据交易平台需尝试为数据需求者和数据供给者搭建供需交易平台,通过提供交易撮合服务,实现供需双方直接进行数据交易,如天元数据交易平台和数粮交易平台都提供了数据供需撮合服务,而贵阳大数据交易所提出建立数据需求在线撮合平台。
在医疗健康领域,随着可穿戴健康设备、物联网和大数据技术的发展,实时监测个人身体活动状况(如运动强度)、认知状态(如个人情绪)和生理状态(如血压、呼吸频率和心率等)成为日常生活中的一部分[2-3]。目前,市场上各种健康应用程序(Health-App)多达16.5 万个,有超过一半的智能手机用户通过这些健康应用程序监测自身的健康状况[4]。此外,市场上也出现了许多健康数据需求者(如健康研究中心、医药公司和医疗服务机构等),希望获得海量的个人健康数据,从而满足各种应用研究以及提供更合理的健康服务。然而,通过市场调查发现,个人生成的健康数据散落在各可穿戴健康设备或相应的健康应用程序中,没有进行统一地收集和管理[5]。考虑到个人健康数据的隐私性及潜在的经济、社会价值,健康数据需求者往往无法获得海量的个人健康数据,进而导致无法实现对个人健康数据价值进行充分地挖掘。因此,在这种市场环境下,数据交易平台为健康数据需求者获取个人健康数据搭建起交易的桥梁,有效地促进了个人健康数据的市场流动。然而,进行个人健康数据交易需通过“群智感知(Crowdsensing)”模式进行,即通过个人所持的可穿戴健康设备进行感知、收集自身健康数据。在个人健康数据收集过程中,个人,即健康数据的所有者,理性地决策是否共享自身的健康数据。换句话说,当数据交易平台提供的交易价格较高(较低)时,健康数据所有者将供给较多(较少)的健康数据,即存在健康数据供给不确定性。同理,对于健康数据需求者也存在相似的需求不确定性问题。从现实出发,要促进个人健康数据交易,数据交易平台面临如下挑战:(1)在通过群智感知模式进行个人健康数据收集时,健康数据所有者的感知成本受所持可穿戴健康设备和感知行为等影响,呈现隐私性和差异性特征,不能进行准确地预估[6];(2)在进行个人健康数据交易过程中,个人除了获得外在奖励报酬(例如金钱奖励)外,同时将获得一定的内在收益,其影响数据交易平台制定公平合理的定价策略[7];(3)健康数据所产生的效用为健康数据需求者的隐私信息,导致数据交易平台无法准确地获知。因此,针对这种信息不对称下健康数据供需不平衡问题,数据交易平台需要设计一种公平合理的双边交易定价策略,以实现健康数据所有者与健康数据需求者之间的供需匹配。
关于平台双边定价问题,绝大多数文献集中于各类产品或商品等实物定价,通过构建相应的效用函数模型,采用博弈论和优化理论等方法研究最优定价策略。不同于实物交易,数据具有重复供给和效用不确定性等特点,这使得现有的相关定价理论与方法不能直接应用于数据交易中。因此,近年来,相关学者从不同的视角出发开始对数据交易定价问题进行探究。Jang 等构建了“多对一”的数据交易框架,整合拍卖方法和Stackelberg 博弈模型为数据交易平台设计了最优的交易定价策略[8]。Shen 等采用Stackelberg 博弈模型分析了数据提供者、服务提供者和数据使用者三者间的交互关系,设计了最大化服务提供者利润的交易定价机制[9]。Oh等基于对个人数据共享意愿和数据消费者购买意愿的分析,设计了个人数据交易机制并提出采用梯度上升算法计算最优的数据交易价格[10]。同时,Oh 等以数据交易链中的数据提供者、数据中介、服务提供者和数据消费者为主体,分析研究了数据中介收益最大化、服务提供者收益最大化及数据中介与服务提供者间的非合作竞争博弈问题[11]。Jiao 等采用贝叶斯数字商品拍卖方法,以数据服务为交易对象,通过设计交易机制研究了最优的数据服务交易价格和交易量[12]。Cao 等以数据所有者、数据收集者和数据使用者为研究对象,通过对数据交易流程分析,以社会福利最大化为目标,提出采用迭代拍卖的方法进行数据交易定价[13]。从交易模式的角度来讲,上述学者研究的是数据交易平台先购买原始数据,经加工处理后,再以适当的价格出售数据信息或服务。不同于上述学者研究的数据交易模式,Bataineh 等设计了按照数据交易成功次数进行收费的定价机制[14]。Niu 等基于对数据提供者可接受价格的预估,设计了一种动态的数据检索定价机制,从而实现数据交易平台累积检索收益最大化[15]。通过对上述文献的梳理和分析后发现,学者们多采用简化的方式来描述交易者之间的交易意愿或者假设参与数据交易的利益相关者具有完全信息,而尚未在信息不对称视角下开展有关健康数据交易双边定价策略的研究。
近年来,在智能电网、移动通信、可再生能源和共享经济等领域,相关学者提出采用迭代双边拍卖方法解决双边信息不对称下参与者间的竞争博弈问题[16-18]。当采用双边拍卖方法时,拍卖者失去了传统单边拍卖中的垄断性和相对优势,使得参与拍卖双方关系变成一种供给与需求关系。此外,采用双边拍卖方法可避免直接获取交易双方的个人隐私信息,实现交易双方的收益最大化。因此,本文提出采用迭代双边拍卖方法设计健康数据交易任务分配规则和定价/奖励规则,撮合健康数据所有者与健康数据需求者直接进行健康数据交易,实现健康数据市场的供需平衡。借鉴相关参考文献,采用迭代双边拍卖方法的流程为:健康数据所有者和健康数据需求者依据给定的任务分配规则和定价/奖励规则向数据交易平台提交数据的供给报价和需求报价,平台则根据交易双方的报价以健康数据交易系统收益最大化为目标进行数据交易任务分配;接下来,数据交易平台判断市场是否达到出清,若否,调整任务分配规则和定价/奖励规则,健康数据所有者和健康数据需求者重新提交供需报价;重复上述过程,直到健康数据交易市场达到出清状态,迭代终止。综上,通过采用迭代双边拍卖方法,一方面可有效解决双边信息不对称下数据交易平台无法直接获取健康数据交易双方收益函数信息的难题;另一方面可以设计出公平合理的个人健康数据交易双边定价策略,实现健康数据所有者和健康数据需求者的收益最大化,为平台开展数据交易撮合服务提供支持。
1 问题描述和模型构建
假设数据交易平台上有M 位健康数据所有者与N 位健康数据需求者进行健康数据交易。考虑到健康数据所有者收集自身健康数据过程中存在身体疲劳、消耗可穿戴设备的电量、占用个人时间和隐私泄露风险等,健康数据需求者需要提供奖励报酬,以激励健康数据所有者愿意主动共享自身健康数据。不同于其他行业或领域的数据交易,在个人健康数据交易过程中,健康数据所有者也增强了对自身健康状况的了解,获得一定的内在收益[19]。根据双边拍卖理论与方法,当数据交易平台发布了N 位健康数据需求者的数据需求后,健康数据所有者m,m=1,2…,M需要决策最大化自身收益的数据供给报价,即:

其中,am={am1,am2,…,amN}为健康数据所有者m,m=1,2,…M向平台提交的数据供给报价,即期望获得的最低奖励报酬;xm={xm1,xm2,…,xmN}为平台分配给健康数据所有者m,m=1,2,…M的数据交易任务;Φm(am,xm)和Um(xm)分别为健康数据所有者m,m=1,2,…M共享自身健康数据后获得的外在奖励报酬和内在收益;Cm(xm) 为健康数据所有者m,m=1,2,…M在感知自身健康数据过程中付出的成本。根据实践经验,若健康数据所有者供给的健康数据越多,其付出的成本越多,同时获得的内在收益也越大,故假设Cm(xm) 为连续单调递增可微的凸函数,Um(xm) 为连续单调递增可微的凹函数[20]。此外,考虑到可穿戴健康设备电池电量和个人感知时间的有限性,每位健康数据所有者存在一个最大的数据供给量。约束条件(2) 表示健康数据所有者m,m=1,2,…M向健康数据需求者n,n=1,2,…,N可供给的数据量不超过其最大供给量lm。
由于存在信息不对称及数据交易市场中缺乏标准的数据交易定价机制,使得健康数据需求者无法准确预测健康数据所有者可接受的最低交易价格。因此,根据双边拍卖理论与方法,当健康数据需求者n,n=1,2,…,N通过数据交易平台购买健康数据时,需向平台提交最大化自身收益的数据购买价格——需求报价,即:

其中,yn={y1n,y2n,…,yMn}为数据交易平台分配给健康数据需求者n,n=1,2,…,N的数据交易结果;Vn(yn) 为健康数据需求者n,n=1,2,…,N的效用函数。一般情况下,健康数据需求者从健康数据所有者处购买的健康数据越多,健康数据产生的效用越大,但随着购买的健康数据数量不断增加,边际效用不断降低,故假设Vn(yn) 为连续单调递增可微的凹函数。bn={b1n,b2n,…,bMn}为健康数据需求者n,n=1,2,…,N向平台提交的需求报价;Pn(bn,yn) 为健康数据需求者n,n=1,2,…,N向平台支付的数据购买费用。约束条件(5) 表示健康数据需求者购买的数据量不超过健康数据所有者可供给的数据量。在现实中,健康数据需求者往往会设定一个最低的数据需求量,约束条件(6) 表示健康数据需求者n,n=1,2,…,N购买的数据量大于等于其设定的最低数据需求量kn。
基于上述模型的分析,数据交易平台需要协调健康数据所有者与健康数据需求者间利益冲突,使得参与交易的健康数据所有者和健康数据需求者实现收益最大化。从系统角度出发,整个健康数据交易系统的收益为所有健康数据所有者与所有健康数据需求者的收益之和[21-23]。要协调健康数据所有者与健康数据需求者间利益矛盾,数据交易平台需要最大化整个健康数据交易系统收益,即:

根据Vn(yn),Um(xm) 和Cm(xm) 的函数性质,并结合约束条件是关于xmn,ymn的线性函数,可知上述优化问题为凸优化问题,存在唯一最优解。根据KKT 条件,引入松弛变量,则上述优化问题的Lagrangian 函数为:

其中,λ≜[λmn]M×N,λmn≥0;μ≜[μmn]M×N,μmn≥0;η≜(η1,η2,…,ηN),ηn≥0 分别是约束条件(9),(10) 和(11)相对应的松弛变量。因此,要实现整个健康数据交易系统收益最大化,最优的健康数据交易分配结果,m=1,2,…,M,n=1,2,…,N需满足如下KKT 条件:

由于函数Vn(yn),Um(xm)和Cm(xm) 分别是健康数据需求者和健康数据所有者的个人隐私信息,数据交易平台无法获知这些函数的具体表达式。换句话说,数据交易平台与健康数据所有者和健康数据需求者之间存在双边信息不对称,无法通过计算上述KKT 条件获得最优的健康数据交易分配结果,即求解健康数据交易系统收益最大化问题是一个NPhard 问题。另外,健康数据所有者和健康数据需求者都追求自身收益最大化,可能存在与健康数据交易系统收益最大化目标不一致。因此,即便借助相关优化工具获得了实现健康数据交易系统收益最大化的交易分配结果,也不能确保在实践中顺利的实施。因此,面对这种双边信息不对称的问题,下文采用了迭代双边拍卖方法来解决健康数据交易系统收益最大化问题[24-25]。
2 健康数据交易双边定价策略
数据交易平台的目标是通过对健康数据交易任务进行合理分配,撮合健康数据所有者与健康数据需求者成功地进行健康数据交易,实现整个健康数据交易系统收益最大化。迭代双边拍卖方法为数据交易平台提供了有效的解决方法,避免直接获取健康数据交易双方的隐私信息。采用迭代双边拍卖方法的具体流程如下:
步骤1:数据交易平台向健康数据所有者和健康数据需求者公布交易任务分配规则和定价/奖励规则,健康数据所有者和健康数据需求者分别求解收益最大化问题(1)和(4),然后向平台提交健康数据的供给报价和需求报价;
步骤2:数据交易平台根据设定的交易任务分配规则和交易双方提交的供需报价,计算交易分配结果;
步骤3:数据交易平台判断市场是否达到出清状态。若否,平台调整交易规则,健康数据所有者和健康数据需求者依据调整后的交易规则开始新一轮的报价;
步骤4:重复上述步骤,直到市场达到出清状态。
健康数据交易过程中的迭代交互框架,如图1 所示。

图1 健康数据交易迭代交互框架Figure 1 The interaction framework of health data trading
2.1 健康数据交易任务分配机制
借鉴相关文献提出的分配规则[26-27],假设数据交易平台采用如下形式对健康数据交易任务进行分配:

其中,约束条件与健康数据交易系统收益最大化问题中的保持一致。根据目标函数是凹函数且约束条件是关于xmn和ymn的线性函数,优化问题(22)是一个凸优化问题,存在唯一最优解。根据KKT 条件,该优化问题的Lagrangian 函数为


通过对KKT 条件(24)~(31)进行分析,可获得如下相关的命题。
命题1健康数据所有者m,m=1,2…,M和健康数据需求者n,n=1,2,…,N的数据供给量和需求量分别为
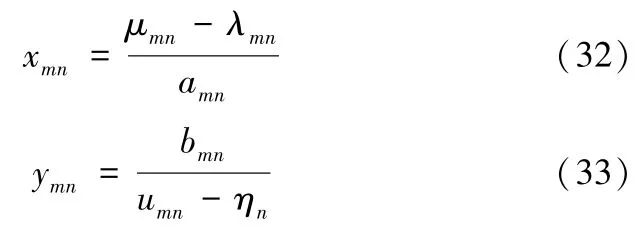
证明:根据上述KKT 条件,数据交易平台将按照式(24)和式(25)分配健康数据交易任务。证毕。
通过对命题1 进行分析可发现,数据交易平台在进行交易任务分配时遵循如下原则:健康数据所有者提交的供给报价越高,分配的交易任务越少,反之分配的交易任务越多;健康数据需求者提交的需求报价越高,获得的健康数据量越多,反之获得的健康数据量越少。
命题2当健康数据所有者提交的供给报价和健康数据需求者提交的需求报价分别为
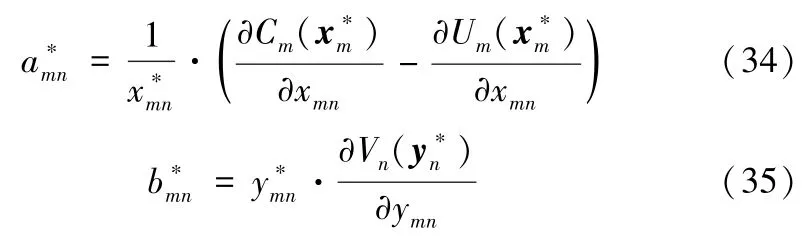
时,可实现健康数据交易系统收益最大化。
证明:由于优化问题(8)和(22)的目标函数都是凹函数且具有相同的约束条件,使得两个优化问题的KKT 条件等价,从而在计算最优解时满足分别等于。因此,分别联立(14)和(24),(15)和(25),可计算得出(34)和(35)。证毕。
2.2 健康数据所有者和健康数据需求者的最优定价策略
当按照式(32)和式(33)进行交易任务分配时,数据交易平台需要设计合理的定价/奖励规则,使得健康数据所有者和健康数据需求者按照式(34)和式(35)提交健康数据的供给报价和需求报价,进而实现健康数据交易系统的收益最大化。
根据数据交易平台对健康数据所有者m,m=1,2…,M分配的交易任务(32),健康数据所有者m,m=1,2…,M面对的优化问题(1)变成

对目标函数关于amn求一阶导数可得
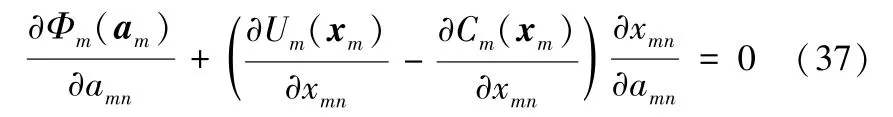
由式(32)关于amn求一阶导数可得

结合KKT 条件中的(14),整理可得

因此,要引导健康数据所有者m,m=1,2…,M按照式(34)提交供给报价,数据交易平台对健康数据所有者设计的最优定价策略为
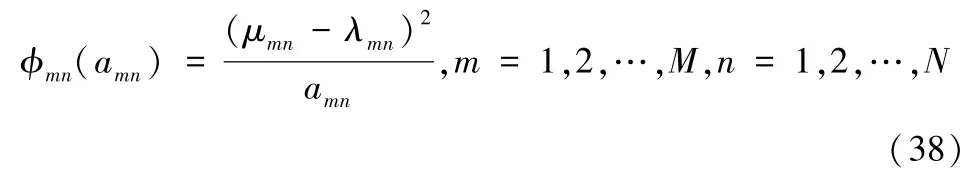
进一步,数据交易平台向健康数据所有者支付的奖励报酬为

显然,数据交易平台向健康数据所有者设计的定价策略与健康数据所有者提交的供给报价呈负相关关系,换句话说,当健康数据所有者期望通过提交较高的供给报价,以期获得较高的奖励报酬时,最后却获得较低的奖励报酬。
根据数据交易平台对健康数据需求者n,n=1,2,…,N分配的数据交易量(33),健康数据需求者n,n=1,2,…,N需要决策的优化问题(4) 变成

同理,对目标函数关于bmn求一阶导数可得

由式(33)关于bmn求一阶导数可得

结合KKT 条件中的(15),整理可得

因此,要引导健康数据需求者n,n=1,2,…,N按照式(35)提交需求报价,数据交易平台向健康数据需求者设计的最优定价策略为

进一步,数据交易平台向健康数据需求者收取的数据交易费用为
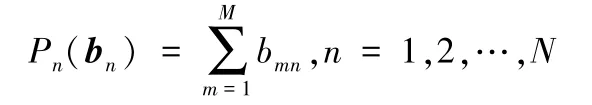
显然,数据交易平台为健康数据需求者设计的定价策略等于健康数据需求者所提交的需求报价。
综上,当数据交易平台对健康数据所有者m,m=1,2…,M和健康数据需求者n,n=1,2,…,N设计的交易定价策略为式(38)和式(41)时,健康数据所有者m,m=1,2…,M提交的供给报价为(34),健康数据需求者n,n=1,2,…,N提交的需求报价为(35),在最大化健康数据所有者和健康数据需求者收益时,实现整个健康数据交易系统收益最大化。
命题3假定Vn(0)=0,Cm(0)=0,Um(0)=0,m=1,2,…,M,n=1,2,…,N,当数据交易平台设定健康数据交易双边定价策略为式(38) 和式(41) 时,健康数据所有者m,m=1,2…,M和健康数据需求者n,n=1,2,…,N获得的收益始终为非负,即
证明:当数据交易平台按照式(38)和式(41)设计健康数据交易双边定价策略时,amn,bmn,xmn,ymn,umn,λmn,ηn分别等于。由Cm(xm) 是凸函数,可得
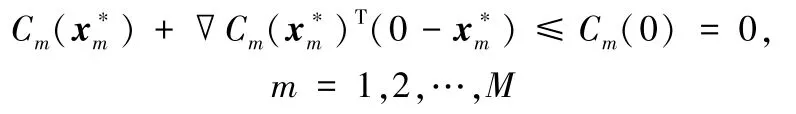
进一步整理,可得

由Um(xm) 是凹函数,可得

进一步整理,可得

联立式(42)和式(43),并结合式(14)和式(24),可得

由Vn(y) 是凹函数,可得

进一步整理,可得

再结合式(15)和式(25),可得
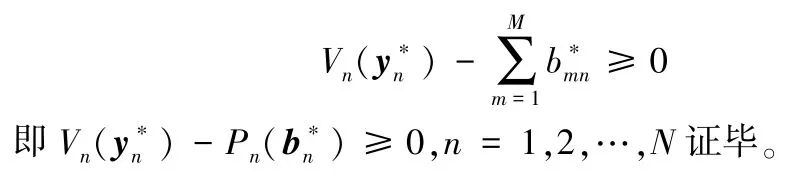
3 设计健康数据交易分布式迭代算法
基于前文的研究与分析,下面设计分布式迭代算法计算实现市场出清的最优健康数据供需报价、双边交易价格和任务分配结果,具体的算法如下所示:


当迭代步长α较小时,上述分布式迭代算法可视为关于t的连续性算法。由λmn≥0,m=1,2,…,M,n=1,2,…,N对式(44) 进行如下分析:
由于迭代步长α较小,(44)中的等号右边部分为非负,从而可写成

进一步,可得

假定g,h∈R且h≥0,进行如下定义
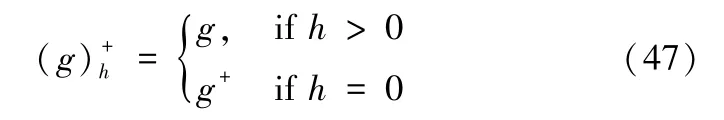
因此,可以获得

命题4假设迭代步长α极小,所设计的健康数据交易分布式迭代算法将使任意(x,y) 和(λ,μ,η) 收敛到最优值(x*,y*) 和(λ*,μ*,η*),从而实现整个健康数据交易系统收益最大化。
证明:定义Lyapunov 函数

对H(λ,μ,η) 关于时间t求一阶导数,可得


根据前文计算的健康数据交易任务分配结果,将式(38)代入式(36)后,可得
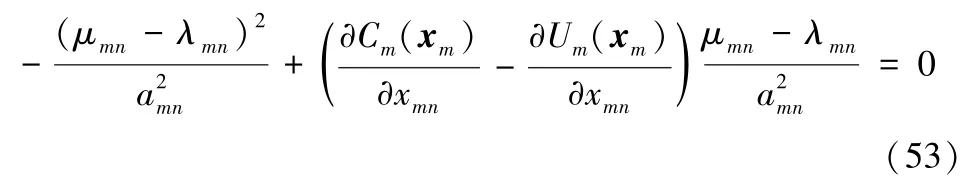
整理得

同理,可计算得出
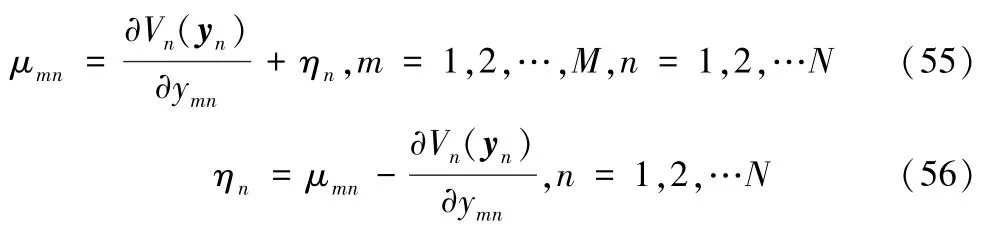
因此,将式(14)和式(54)代入下面等式,可得


同理,将式(15)和式(55)代入下面等式,可得


由Vn(yn) 和Um(xm) 是凹函数,Cm(xm) 是凸函数,根据凹函数和凸函数的函数性质,可得

因此,结合式(62),(63)和(64),通过对式(57),(58),(59),(60)和(61)进行累加,可得

4 算例研究
数粮平台是一个大数据领域的流通平台,为数据供需双方搭建起交易桥梁。目前平台已实现对数据、大数据应用产品和服务等交易,涵盖API 接口、数据包下载和定制等交易模式,预期打造一个实效的数据集散地。随着物联网、可穿戴设备和大数据技术的发展,个人数据交易逐渐成为数粮平台的重要业务组成部分。在数粮平台上开展个人数据交易流程为:(1)“发布需求”,数据需求者提交数据需求信息,包括获取方式、交付方式、交易限制和投标信息等,经数粮平台审核通过后,在需求大厅公布数据需求;(2)“按需定制”,感兴趣的平台用户进入需求大厅选择一项需求后,填写投标信息,点击“我要接单”,若数据需求者满意用户提交的数据样本和投标价格,后面自动进入订单流程操作,否则等待新一轮报价进入。本文以数粮平台为背景,通过计算分析验证所提出的健康数据交易双边定价策略的有效性。
假设数粮平台上有2 位健康数据需求者(D)和3 位健康数据所有者(S)进行健康数据交易。根据前文有关Vn(yn),Cm(xm)和Um(xm) 函数性质的设定,假定健康数据所有者的感知成本函数、内在收益函数及健康数据需求者的效用函数分别采用如下形式:

其中,βmn≥0,φmn≥0 和δmn≥0 分别为健康数据所有者m=1,2,3 的成本系数、内在收益系数和健康数据需求者n=1,2 的效用系数。假定健康数据需求者n=1,2 的最低数据需求量为D1=D2=5,设定ε=0.001,α=0.01,k1=k2=5,其他参数的初始化取值见表1 所示。

表1 相关参数初始化取值Table 1 Initialization value for related parameters
通过MATLAB_R2016a 进行计算时,引入相对误差error=,其中F为Frobenius 范数。图2(a)表示随着迭代次数不断增加,健康数据所有者和健康数据需求者所提交供需报价的相对误差不断减小,验证了本文所设计的健康数据交易分布式迭代算法的收敛性。
考虑到健康数据所有者成本系数βmn,内在收益系数φmn及健康数据需求者效用系数δmn对不同个体的差异性,本文对试验结果进行了比较分析。图2(b)是健康数据所有者S1的供给报价迭代过程,迭代初期S1 对D1 和D2 的报价基本相同,随着迭代次数的增加,差异不断变大,在收敛时S1 对D1 的报价明显低于对D2 的报价。图2(c)是健康数据需求者D1 的需求报价迭代过程,在迭代初期D1 对S1,S2 和S3的报价差异较小,随着迭代次数的不断增加差异不断变大,最后收敛于不同的需求报价。图2(d)和图2(e)为数据交易平台对健康数据所有者和健康数据需求者的数据交易任务分配,随着迭代次数的不断增加都逐渐收敛于稳定状态。通过对图2(b)与图2(d)联合分析可发现,当健康数据所有者提交的供给报价越高,数据交易平台分配给健康数据所有者的交易任务越小;同理,通过对图2(c)与图2(e)联合分析可发现,当健康数据需求者提交的需求报价越高,数据交易平台分配给健康数据需求者的交易任务越大。图2(f)为健康数据所有者S1,S2,S3 与健康数据需求者D1 之间的数据供需差异的收敛结果,可以发现大概经过15 次迭代后健康数据的供需差异基本趋于零。

图2 算法收敛结果Figure 2 The convergence results of algorithm
表2 为健康数据交易分布式迭代算法收敛后的均衡结果,可以发现健康数据所有者和健康数据需求者所提交的供给报价和需求报价均为差异化报价,而健康数据所有者的数据供给等于健康数据需求者的数据需求。此外,通过将Φ1,Φ2,Φ3及P1,P2进行相加,可以获得Φ1+Φ2+Φ3=P1+P2,即所有健康数据所有者获得的外在奖励报酬之和等于所有健康数据需求者支付的数据购买费用之和。

表2 算法收敛后的均衡结果Table 2 The equilibrium results after algorithm convergence
5 结束语
设计公平合理的健康数据交易双边定价策略,有利于解决健康数据供需矛盾,推动健康数据的市场流动。考虑到数据交易平台与健康数据所有者和健康数据需求者之间存在双边信息不对称,本文采用迭代双边拍卖方法设计了健康数据交易任务分配规则及相应的定价/奖励规则,以撮合健康数据所有者与健康数据需求者进行交易,实现整个健康数据市场的供需平衡。然后,通过设计健康数据交易分布式迭代算法计算实现市场出清的最优健康数据供需报价、双边交易价格和任务分配结果。研究结果表明健康数据所有者的最优交易价格与其提交的供给报价呈负相关关系,而健康数据需求者的最优交易价格等于其提交的需求报价。本文在刻画健康数据所有者收益函数时增加了对健康数据所有者内在收益的度量,同时在约束条件上考虑了个人健康数据的非排他性,这在以往的研究文献中尚未涉及。从实践角度,研究结论为指导数据交易平台撮合健康数据所有者与健康数据需求者进行健康数据交易提供了有效支持。
虽然本文从信息不对称视角出发对个人健康数据交易定价策略进行了研究,但本文还存在许多需要进一步完善的地方,如尚未研究健康数据所有者和健康数据需求者进行交易价格预测的情景;在构建健康数据需求者收益函数时尚未考虑网络效用和健康数据质量等影响。学者有必要在未来开展更深入和广泛的研究,以期进一步提高研究结论的有效性和可靠性。

