基于SBD技术的小水线面双体船首尾鳍优化设计

鲍家乐，倪其军，李胜忠

（中国船舶科学研究中心，江苏无锡 214082）

0 引 言

首尾鳍作为小水线面双体船（small water-plane-area twin hull,SWATH）的重要组成部分，具有增加航态稳定性、调整航行姿态以及改善耐波性等作用，是SWATH 设计过程中至关重要的一环。作者参与了一艘6 000 吨级小水线面双体船的设计任务，该船目前已经完成了主船体的线型优化工作，其阻力性能优越[1]。在使用母船型船变换方法设计首尾鳍时发现，初始方案中首尾鳍需要较大面积和攻角角度才能保证该船在设计航速点航行姿态为尾倾，且总阻力大幅增加约35.8%。因此，需要对该首尾鳍进行优化设计。

首尾鳍的设计最早采用试验测定和母型船变换的方法，随后又发展为根据运动稳定性判据保证其纵向运动稳定性，再通过优选方式获得阻力和姿态能接受的方案。最近几年，又有多位专家学者通过自动控制理论对首尾鳍进行优化设计。苗飞等[2]通过小水线面双体船的纵向运动方程和稳定性判别准则，提出了一种首尾鳍设计方法，针对某小水线面双体船进行了首尾鳍设计工作，并与模型试验相互验证，取得较好结果；高占胜等[3]在小水线面双体船纵向运动稳定性判据的基础上，分析了首尾鳍的安装位置、鳍面积等参数变化对该型船不同航速时纵向运动稳定性的影响及规律；Arifah Ali 等[4]在深水中对安装有首尾鳍的半小水线面双体船模型进行了静水阻力试验，研究了首尾鳍角度对阻力和船体周围流动的影响。这些方法在工程实践中发挥了巨大作用，解决了很多工程问题，但在面对本文工程实际问题时，遇到一些困难。比如首尾鳍安装位置受主船体线型制约，首尾鳍采用成熟产品而导致翼型难有较大变化等问题，很难继续采用传统设计方法进行优化。而近年来所出现的基于SBD（simulation based design）技术的构型优化设计方法，能够在给定约束条件下，以性能最优为目标自动求解优化设计问题，可为本文首尾鳍的优化提供一个新思路。

本文将已用于船型优化设计的SBD 技术[5-6]引入到首尾鳍设计中，建立以性能最优为目标来驱动小水线面双体船首尾鳍优化设计的方法，并将其应用于目标船首尾鳍的优化设计中。以该船的阻力性能最优为优化目标，选择首尾鳍面积大小、攻角角度和襟翼形式等参数作为设计变量，在主潜体线型不变的前提下，以小水线面双体船运动姿态作为约束条件，结合多目标粒子群全局优化算法，综合集成优化流程，自动优化得出小水线面双体船首尾鳍的优化设计方案。

1 目标船概况

本文目标船为一艘6 000 吨级小水线面双体船，其外形如图1 所示，主要参数见表1，计算模型缩尺比为1:25。根据该船模型试验结果，在加装首尾鳍后，该船总阻力大幅增加，主要原因是鳍的升阻比过小，需要较大面积和攻角才能提供足够升力调整姿态。因此，需要对该首尾鳍进行优化。

图1 SWATH船示意图Fig.1 Schematic diagram of SWATH

表1 SWATH船主要尺度参数Tab.1 Principal dimensions of SWATH

2 基于SBD技术的首尾鳍优化设计方法

基于SBD 技术的首尾鳍优化设计方法以优化流程自动化为特点，主要由基于RANS 方程的水动力性能评估技术、首尾鳍几何变形技术、最优化技术和综合集成技术等组成。

2.1 基于RANS方程的水动力性能评估技术

水动力性能评估技术是整个优化技术的基础，其预报精度是确保设计优化结果的关键因素。本文采用基于RANS 方程的高精度粘流数值评估软件，结合重叠网格技术，对目标船阻力性能和运动姿态进行预报，其可靠性在多个船型设计中已经得到了应用与验证，具体评估流程可参见文献[7-8]。

本文首先对该船进行水动力性能预报，将裸船体、首尾鳍、舵以及背景流域进行单独划分，然后生成计算网格，如图2所示。再将各个部分进行合并，构成一个完整的小水线面双体船全附体重叠计算域。然后采用二因次傅汝德法换算到实船后与模型试验结果进行对比验证，如表2所示。

图2 重叠计算网格Fig.2 Overlap grid of SWATH

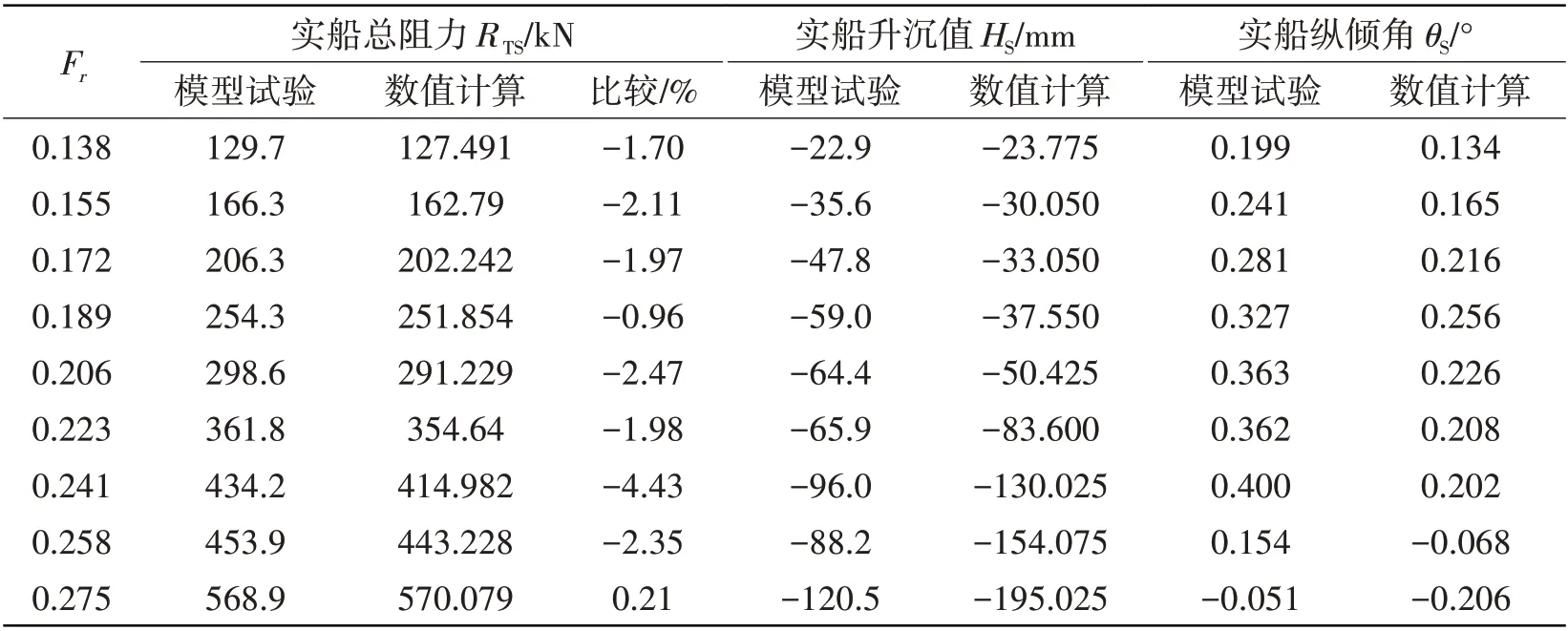
表2 数值计算与模型试验结果对比Tab.2 Numerical and experimental results of SWATH

对比结果表明，通过数值计算得到的总阻力误差基本在3%以内，升沉值和纵倾角趋势与模型试验结果基本一致，验证了本文所采用的水动力性能评估技术是可靠的。

2.2 最优化技术

最优化技术也是首尾鳍优化设计技术中的关键之一，是指导优化设计方向的主要技术手段。本文最优化技术采用多目标粒子群全局优化算法，该算法已在船型优化设计中得到了应用[5-6]。

2.3 首尾鳍参数化表达与变形技术

首尾鳍参数化表达与变形技术是SBD 优化技术的前提条件。本文选择基于CAD 的变形方法和自由变形方法（free-form deformation approach,FFD）作为几何变形重构方法[8]，并采用计算网格自适应技术[9]，使首尾鳍计算网格能够随鳍外形变化而自适应变化。

2.4 综合集成技术

保证首尾鳍优化设计流程能够自动进行的关键技术就是综合集成技术，它也是将优化设计方法中各个模块串联起来的主干。本文采用C++语言将以上各个模块的输入与输出进行连接交互，按照优化流程进行迭代整合，最终建立起一个完整有序的优化设计平台。

3 首尾鳍优化设计

本文采用基于SBD技术的首尾鳍优化设计方法，针对6 000吨级小水线面双体船首尾鳍进行优化设计，解决该船在加装首尾鳍后在经济航速点模型总阻力增加35.8%，以及在设计航速点出现埋首现象的问题。

3.1 优化对象

本文的优化对象为6 000 吨级小水线面双体船首尾鳍，其外形如图3 所示。首尾鳍的面积大小、安装位置、角度均采用上文中模型试验结果。

图3 SWATH船首尾鳍示意图Fig.3 Schematic diagram of stabilizing fins of SWATH

3.2 目标函数

本文针对小水线面双体船阻力性能进行优化，选择在小水线面双体船的经济航速（11 kn）与设计航速（15 kn）点对首尾鳍进行优化设计。将这两个点的阻力值作为目标函数，如下式所示：

式中，F1、F2为构建的目标函数，Rt1为小水线面双体船在11 kn 时的总阻力，Rt2为其在15 kn 时的总阻力，Rt10为初始方案11 kn时的总阻力，Rt20为初始方案15 kn时的总阻力。

3.3 设计变量

参考首尾鳍相关文献以及本船工程实际情况，本文选择首尾鳍面积和攻角作为设计变量，再通过增加襟翼和改变后掠角进一步提高升阻比（首尾鳍襟翼形式如图4所示，襟翼变化如图5所示）。考虑到尾鳍襟翼会影响桨盘面处的伴流，进而影响推进效率，故襟翼仅选定在首鳍处进行添加。

图4 首尾鳍襟翼形式Fig.4 Diagram of wing flap of fins

图5 首尾鳍襟翼变化Fig.5 Variation of angles of wing flap of fins

因此，文中首尾鳍的设计变量选择为首鳍的面积S1、首鳍主翼的攻角角度α1、首鳍襟翼的攻角角度β、首鳍的前缘后掠角γ1、尾鳍的面积S2、尾鳍的攻角角度α2和尾鳍的前缘后掠角γ2。

3.4 参数化表达变形

基于SBD技术的首尾鳍优化设计方法的核心在于如何实现首尾鳍自动变形重构。

本文首先采用FFD 自由变形方法，将首尾鳍置入控制体框架内。将控制体外侧剖面内所有的控制顶点沿着首尾鳍长度方向进行平移，然后通过逐层线性插值的方式，将控制体最外侧控制顶点变化向内侧传递，实现后掠角变化，如图6 所示。将襟翼与主翼进行分割（尾弦比为0.25），采用基于CAD直接方法将襟翼部分的所有控制顶点坐标绕襟翼轴中心进行旋转，再将襟翼前端与主鳍末端进行连接修饰，完成首尾鳍襟翼变化。通过网格生成软件Gridgen 宏文件（fin_modify.glf）直接将首尾鳍表面控制顶点进行缩放和旋转，即能实现首尾鳍面积和主翼攻角的调整，如图7所示。

图6 首尾鳍后掠角变化Fig.6 Sweepback variation of fins

图7 首尾鳍面积与主翼攻角变化Fig.7 Variation of areas and attack angles of fins

在首尾鳍的形状发生变化后，采用计算网格自适应技术将计算网格与首尾鳍的几何外形结合起来，直接对鳍表面网格（首尾鳍几何外形）进行自动变形重构，使得整个计算网格能够跟随首尾鳍表面网格发生变化的同时一起自适应变化。这样既能保证计算网格的质量，也能提高其适应性。

在完成首尾鳍的体网格变形后，结合重叠网格技术将船体各个部分体网格和背景网格重叠，形成最终完整的计算域。

3.5 约束条件

根据升力公式重新估算首尾鳍面积并参考相关文献[10-12]确定设计变量变化的上下限，以及设计任务需求中对主船体航行姿态的约束，约束条件如表3所示。

表3 约束条件Tab.3 Constraint of optimization

3.6 优化过程

首先将模型试验结果作为初始方案，采用粒子群全局最优算法对设计变量进行调整，通过FFD自由变形方法实现首尾鳍后掠角发生变化，再通过基于CAD的变形方法实现首尾鳍襟翼转动、面积缩放和攻角旋转；在完成面网格修改后，通过计算网格自适应技术获得修改后的首尾鳍计算网格文件；采用重叠网格技术合并成计算域后对小水线面双体船的水动力性能进行计算，获得目标函数值；然后通过目标函数值判断该结果是否满足约束条件，若满足则作为一组可行解，若不满足则需要将其去除；最后判断是否满足迭代停止条件，若满足则结束迭代，若不满足则继续采用粒子群算法获取新的设计变量值，开始下一轮的迭代。

4 首尾鳍优化结果及分析

本文所采用的多目标粒子群优化算法种群粒子数为40，经过9 轮迭代后，目标函数F1、F2趋于收敛，可行解解集如图8 所示。图中“”表示最优解，其连线构成Pareto前沿。

图8 目标函数解集Fig.8 Schematic diagram of target solution set

本文在最优解集中选择了5 个最优解，所对应的目标函数值、设计变量如表4 所示。

表4 首尾鳍优化结果Tab.4 Optimization result of stabilizing fins of SWATH

兼顾目标函数F1和目标函数F2，本文最终选择优化可行解Opt3 作为最终优化方案。最终得到的首尾鳍方案如表5 所示。初始方案与优化方案首尾鳍外形对比如图9所示。

图9 初始方案与优化方案首尾鳍外形对比Fig.9 Comparison of appearances between the optimized plan and original one

表5 初始方案与优化方案首尾鳍参数对比Tab.5 Comparison of parameters of stabilizing fins between the optimized plan and the original one

在优化过程中，为了快速分析优化效果，只在经济航速点与设计航速点进行了阻力性能预报。现对优化方案进行全航速总阻力以及运动状态预报，并与初始方案进行对比，结果如表6所示。

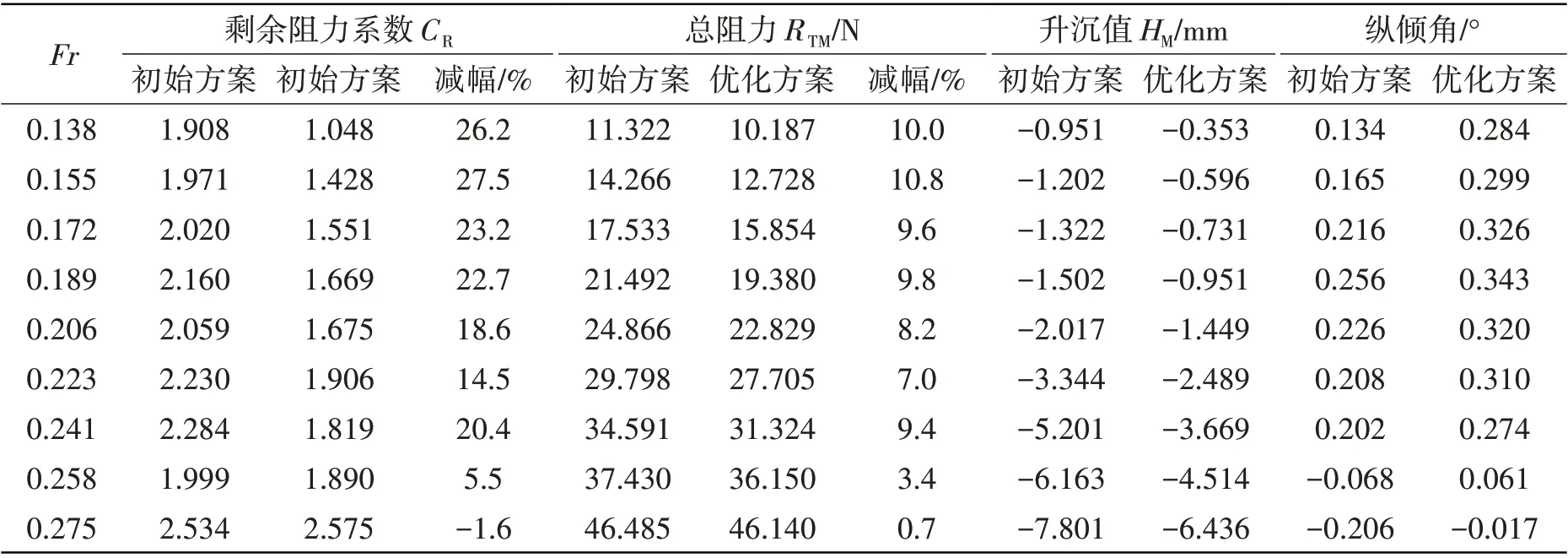
表6 初始方案与优化方案数值预报结果对比Tab.6 Comparison of numerical prediction with the optimized and original plans

通过对比分析可以发现，优化方案在整个航速段中均有减阻收益，在经济航速附近区域（8～11 kn）优化效果较为明显，经济航速点总阻力减少了9.8%，在设计航速区域附近总阻力减幅较小，设计航速点总阻力减少3.4%。

在总阻力减小的同时，小水线面双体船的运动情况也优于初始方案，经济航速点升沉值由-1.502 mm减少为-0.951 mm，纵倾角增加了0.087°；设计航速点升沉值由-6.163 mm 减少为-4.514 mm，纵倾角由-0.068°增加为0.061°。在设计航速点该船的运动姿态已经由首倾状态调整为尾倾状态。

5 结 语

本文将用于船型优化设计的SBD 技术引入首尾鳍优化设计过程中，建立了以性能最优为目标来驱动小水线面双体船首尾鳍优化设计的方法。选取首尾鳍的面积、主翼攻角、襟翼攻角、后掠角等参数为设计变量，在主潜体型线不变的情况下，以经济航速与设计航速总阻力为目标函数，以小水线面双体船运动姿态作为约束条件，采用多目标粒子群优化算法，对6 000 吨级小水线面双体船首尾鳍优化设计问题进行了求解，最终获得了阻力性能与航行姿态较优的设计方案。优化方案总阻力在整个航速范围内均有减小，在经济航速区域收益尤为明显，总阻力减少了约10%。此外，优化使初始方案设计航速点从处于首倾状态转为尾倾状态。