船舶避碰的粒子群-遗传(PSO-GA)的混合优化算法研究
周凤杰
(重庆青年职业技术学院,重庆 400712)
0 引 言
随着世界各国之间贸易往来越来越频繁,船舶海上运输已经成为一种国际性的运输产业,目前全世界大多数国家大宗进出口货物都在使用海上运输,海运航线极为繁忙。同时随着海上科技的发展,船舶吨位越来越大,船速也越来越快,加大了海上碰撞事故发生的可能性。为避免船舶发生碰撞,船舶避碰决策研究已成为航海界关注的重要议题[1-3]。一直以来,许多专家学者都在发表有关避碰自动化、人工智能化的研究成果,目的就是为了避免或减少船舶在海上交通流量大与交通形式复杂情况下发生碰撞事故。经过多年的发展,该领域里的研究已逐步从传统的基于数学理论的分析转变为具有智能化以及学科多样性的路径规划分析,相关领域的学术研究成果也在不断丰富[4-6]。
以模糊逻辑算法为基础,针对船舶碰撞危险度方面,通过计算机模拟的方法,给出了船舶航行避碰操作的决策模型。也有学者针对船舶碰撞危险度进行评估,利用模糊理论得到学习样本,以每个目标的DCPA(Distance of the Closest Point of Approach)和TCPA(Time to the Closest Point of Approach)作为输入,船舶碰撞危险指标作为输出,并应用倒传递神经网络进行多属性决策[7-8]。除了进行船舶避碰的安全决策外,有学者还针对船舶避碰决策中的船舶运动态势和避碰时机,应用灰色理论预测模型,以最近会遇距离及时间为预测参数,实际预测各目标与相对船舶之间在下一刻的运动方向[9-10]。近年来,研究学者开始将人工智能技术引入到避碰领域,利用类神经网络、模糊理论及遗传算法等来进行避碰问题的研究,进而开启了有别于纯数学模式的软件计算自动避碰研究领域。同时针对海上近距离遭遇的船舶,有学者提出避碰技术及路径规划发展分析,以多目标优化算法搜寻最佳航线的路线规划[11-13]。
综合以上研究可以发现,目前关于船舶避碰的研究已经从数学模式进入到系统化模式,从专家系统进入到模糊神经网络及人工智能与决策支持系统,各方面均获得了较有价值的数学模型。但目前针对船舶避碰决策的路径规划研究,大部分是基于检测算法视角,同时采用的优化算法存在收敛过早等问题。为此,本研究在粒子群算法及遗传算法的基础上,建立了船舶避碰路径规划模型,并选用仿真案例进行了验证,克服了优化算法收敛过早等问题,以期为上述避碰决策提供科学合理的理论支持。
1 船舶避碰路径分析
综合文献分析可知[14],避让船在船舶领域被侵犯前,就已经开始采取避让行动。船舶领域为安全距离的集合,故采取行动后与直行船舶间的最小距离为船舶领域。但因航向资料跳动频繁,本研究依据避让行为的阶段性特征,改以两船间最近距离点C为中心,并将最近点前后固定时间区域分成三段(如图1 所示):AB段为发现危险区域段,此时还维持原航向,定义为初始航向;BD段为船舶施展避让动作区域段,定义为避让航向;待他船安全通过后,即在D点回复原航向,将DE段定义为回复航向。当BD段与AB段平均航向差值大于10°,且AB段与DE段误差在3°以内时,即表示有采取避让动作。
从图1 的船舶避碰路径图解中可以看到,与他船最近距离点C前后固定时间内的航向是避碰路径的新航向。为了确定避让的航向以及避让的DCPA 及TCPA,本研究在此取C点前后各2 min 内的航向值做平均;取原航向AB段的避碰动作时间点前的航向值做平均;在回复原航向DE段,因回复时间会较前段采取避让动作时间短,故其航向平均时间的选取可比整段避碰时间区域短。
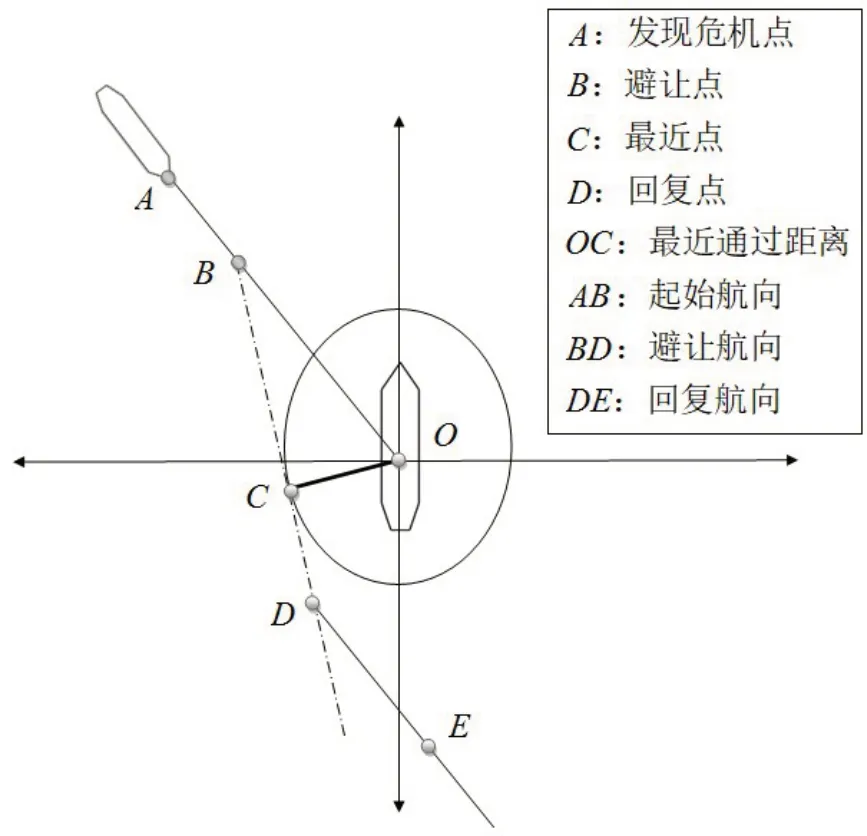
图1 船舶的避碰路径分析Fig.1 Analysis of ship’s collision avoidance path
2 船舶碰撞的条件判定
本系统以用户所设定的DCPA 和TCPA 数值,作为判断是否有碰撞危险以及何时开始执行避碰措施的依据。当两艘船只目前的DCPA 值小于使用者所设定的DCPA 值,且TCPA 大于零时,表示两船继续依此航向前进,否则会有碰撞危险。在有碰撞危机的情况下,当两艘船目前的TCPA 值开始小于使用者所设定的TCPA 值时,开始执行避碰措施。当两艘船目前的TCPA 值开始小于零时,表示已离开两船间的最接近点,无碰撞危险。根据图1 中的船舶避碰路径分析示意图给出船舶碰撞危险判定条件,如表1所示。

表1 船舶碰撞危险度判定条件Tab.1 Determination conditions of ship collision risk
3 船舶避碰算法研究
3.1 PSO算法与GA算法概述
粒子群优化算法(Particle Swarm Optimization,PSO)其主要概念源自于动物群体行为理论,启发于对鸟群及鱼群集体行动的观察,它们集体行动时通过个体之间特殊传递信息的方式,使整个团体能够朝同一方向前进,由此寻求群体最大利益。其算法首先产生初始粒子群,每个粒子都为问题的一个解。而在粒子群搜寻空间中,每个粒子皆有自己的速度,并根据既往经验及群体行为进行演化及修正,逐渐趋近最优解[15]。遗传算法(Genetic Algorithm,GA)是基于生物遗传演化的概念提出的一种优化算法,遗传算法将这样的概念随机选取,接着用随机的突变进化方式来优化所要的条件,作为对船舶碰撞的判断依据。这种方法能够更有效地在一个已知的空间范围内去搜寻新的优化问题,并能寻求最优解。其核心原理就是达尔文所提出的进化论,适者生存,不适者淘汰[16]。
粒子群优化(PSO)算法虽然收敛速度快,但PSO 求解优化时,所有粒子在搜寻时向拥有最佳适应值的粒子方向移动,导致粒子的多样性逐渐降低,而使粒子常常无法跳脱局部最佳解。因此学者提出了动态粒子群优化算法结合遗传算法(PSO-GA),在粒子群求解最优解的过程中结合遗传算法,在符合了特定条件的情况下,将粒子及其位移速度复制并投入交配池中,以交配、突变等机制作为干扰,使粒子能够脱离局部最佳解,而得到全局的最佳解,此混合算法比起传统粒子群算法具有更快的收敛速度,并获得良好的分群质量。在考虑上述两种算法优缺点的基础上整合多目标优化求解,从而能够快速搜寻且脱离局部最佳解,构建和优化船舶路径,避免船舶碰撞。
3.2 避碰路径的编码及初始化
在船舶的避碰路径上,为了获得船舶避让的TCPA 及DCPA 等关键信息,需要实时获得环境信息,来更新船舶的位置及避碰路径的角度。无论是在船舶实时路径的调整还是在初始位置的设定上,都需要凭借环境信息,来确定船舶的位置及避让的角度。因此,在实时路径的调整跟初始位置关系上给定如下方程

式中,n为搜寻参数,pik为目前位置参数。
在空间中设定粒子所要产生的数量,接着再通过这一初始位置以及速度去修正路径移动的位置及速度:

给每颗粒子限制其最大移动速度vmax及最大移动范围pmax,使粒子的速度跟移动不会超出所设定的范围,让控制粒子能在空间范围中均匀地分布。

式中,ri为权重系数,取值为0 <ri<1。
计算每颗粒子的适应性函数,如下列公式所述

式中,wmax与wmin分别代表w的最大值及最小值。
随后利用遗传算法,去调整粒子群中的权重值w。首先决定染色体的范围以及染色体的总量。计算每条单一染色体的适应性,适应性取决于复制过程或选择的染色体,进而产生最初亲代染色体族群(X1,X2,…,Xn),计算每条染色体的适应性(f(x1),f(x2),…,f(xn))。在所有亲代染色体中,以适应性的高低为依据,抽选出我们设定比例数量的染色体,再从这些染色体中找出一对适应性最高的染色体进行交配。通过染色体间的交叉运算以及突变,来产生一对子代的染色体。将新的子代染色体加入新的染色体族群。接着重复步骤,直到染色体总数跟初始总数相等为止。以新的子代染色体取代亲代染色体,直到满足终止条件或是目标已经达到优化。
再次检查粒子的速度限制
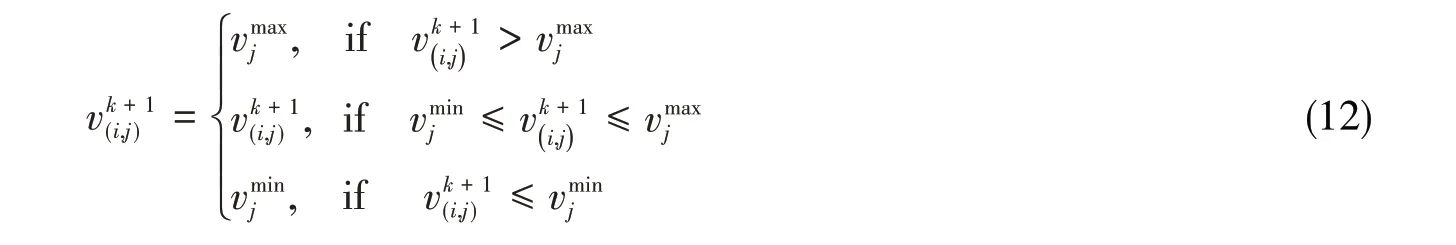
同时更新每颗粒子的位置值:


在搜寻范围中,给每颗粒子一个更新位置值的限制

最后根据粒子最佳位置(PGbest)与最佳适应参数(FGbest)对应的非线性优化目标函数去确定船舶最终避碰路径的移动方式。
3.3 避碰路径优化目标函数
在船舶避碰的决策过程中,既要满足安全性又要满足经济性目标,安全性目标主要是通过DCPA来确定,通过设定最小的DCPA 来确定,经济性通过转向幅度及避让里程来确定,具体的优化目标函数为
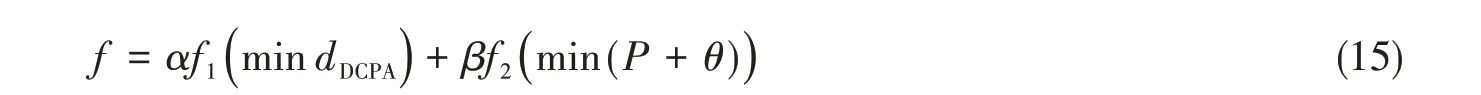
式中,f1为安全性目标函数值,dDCPA表示距离目标船的最近距离,f2为经济性目标函数值,P为避碰路径里程,θ为转向幅度,α和β分别是权重系数,优化目标函数以最小值为优,这样得到的避碰路径安全性及经济性最好。
3.4 避碰路径的程序设计
根据以上的PSO-GA 算法模型及优化目标函数,给出本研究的船舶避碰路径的程序设计流程,如图2所示。

图2 避碰路径程序算法流程图Fig.2 Algorithm flow chart of the collision avoidance path program
4 仿真案例研究
4.1 仿真参数
本研究采用MATLAB 软件进行仿真分析,仿真平台采用INTEL 酷睿3.2 GHz 处理器、内存为16 GB的计算机。风向、水密度等环境参数设置为常规参数,本船和目标船的参数如表2所示。结合给定的船舶参数,本研究结合会遇、交叉以及追越三种情况对船舶避碰进行仿真分析,本船为坐标原点,三类情况的目标船信息如表3所示。

表2 仿真船舶的具体参数Tab.2 Specific parameters of the simulated ship
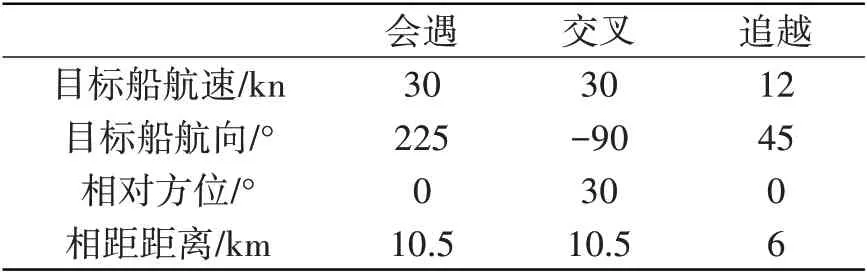
表3 本船和目标船的不同案例信息Tab.3 Different case information of the standard ship and the sample ship
4.2 仿真结果分析
为了验证本研究避碰算法的可靠性,对表3给出的三种船舶避碰情况进行分析,参照目标船的方位角分布及距离,给出避碰状况的初始参数值并输入算法程序,基于初始化函数视角对路径进行初期操作。同时使用混合遗传算法优化船舶避碰路径。使用遗传运算符选择初始群体,使用适度函数确定遗传过程的质量,获得全局优化位置,进而完成对船舶避碰路径的搜索并获得最优避碰操作路径求解。图3 为会遇、交叉和追越三种避碰情况下的船舶避碰路径轨迹分析以及避碰相距距离分析,图3(a)~(c)中虚线表示本船和目标船保持原航速航行时的轨迹,实线为本船的实际避碰路径。图中用圆形表示本船,方形表示目标船。图3(d)为三种避碰情况下的相距距离对比分析。
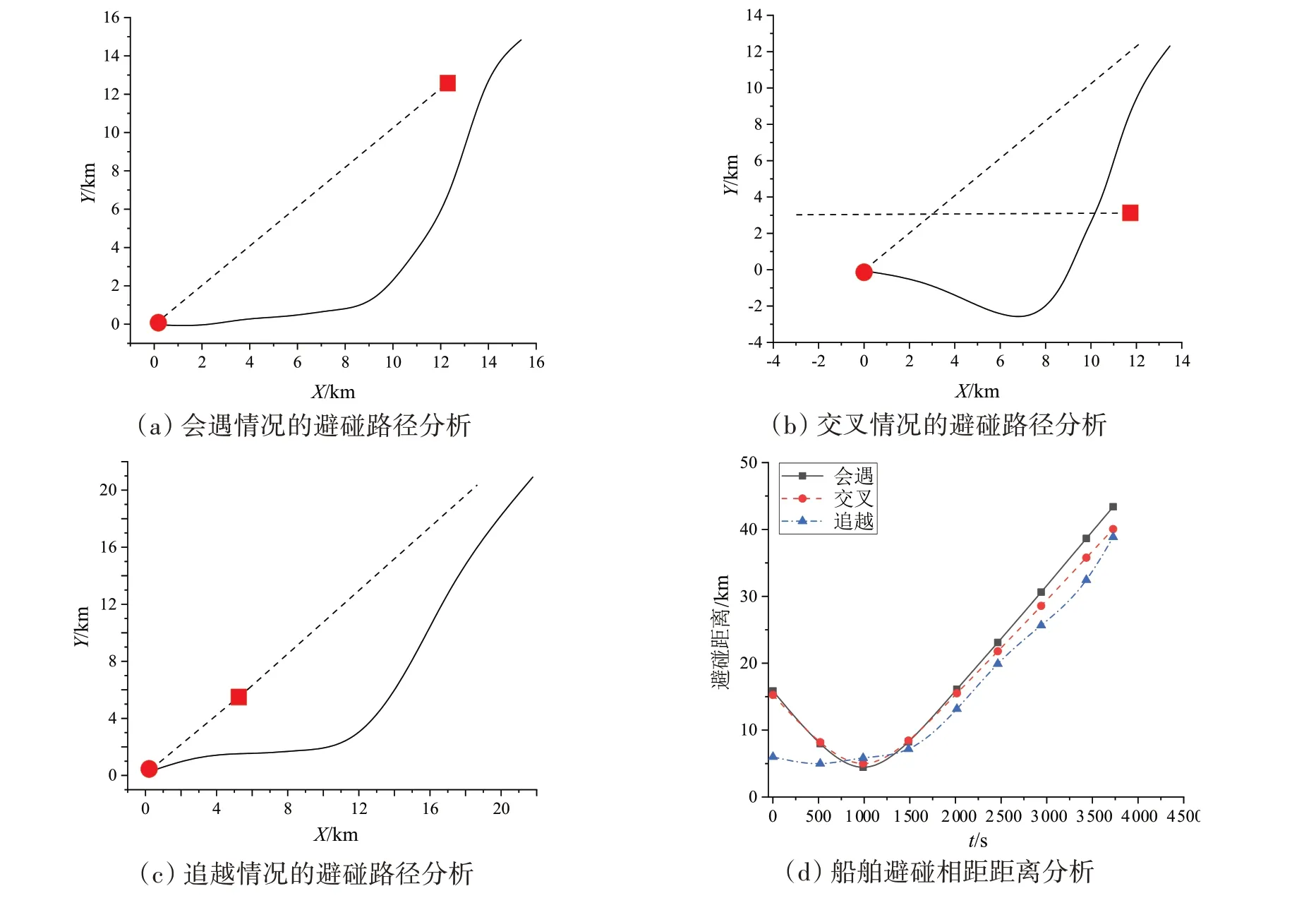
图3 船舶避碰路径分析Fig.3 Path analysis of ship collision avoidance
根据图3 的船舶避碰路径分析可以看到,在会遇、交叉及追越三种避碰情况下,船舶均能实现安全有效的避让,且避让的路径均为平滑,也即本船与目标船之间的距离均匀变化,满足了避碰中的安全性要求,同时从图3(d)的避碰距离可以看到,最小距离均大于5 km,符合了船舶避让中的宽避让要求,同时从路径轨迹中可以看到,三种避碰情况下的目标船最后都接近回到了初始航向轨迹。可见轨迹偏离原航向幅度并不大,满足了船舶避让中的经济性要求。
4.3 算法对比分析
从图3的分析可以看出,本研究算法的避碰路径计划能够满足船舶避碰的安全性及经济性要求,路径的优化性较好,为了进一步验证本研究混合遗传算法的有效性,本研究使用粒子群算法、遗传算法与本研究算法进行对比,对会遇、交叉及追越三种情况进行仿真模拟,并就仿真模拟的迭代次数和平均最优值进行对比,结果如表4所示。

表4 算法的对比分析Tab.4 Comparative analysis of algorithms
根据表4 的对比结果可以看到:在会遇、交叉及追越三种避碰情况下,本研究算法均能在25 次以内完成迭代,其中会遇情况下的迭代次数最少为13 次,这比同样情况下的粒子群算法及遗传算法都少了20次以上,算法的收敛速度也得到了较大的提升;同时从平均最优值上也能看到,本研究算法在会遇、交叉及追越三种避碰情况下的平均最优值均小于粒子群算法及遗传算法,本研究算法的收敛性更好,也即避碰路径的经济性及安全性最优。综上结果,进一步验证了本研究算法的有效性及高效性。
5 结 语
随着海上运输效率的不断提升,船舶碰撞已经成为影响海上运输安全的重要因素之一,对于船舶避碰路径的优化决策分析成为目前研究的热点。本研究综合考虑船舶的安全性及经济性要求,将粒子群算法与遗传算法进行整合,并应用到船舶避碰路径的优化分析中,从而构建船舶避碰路径规划的优化模型,并结合具体案例,在船舶会遇、交叉及追越三种避碰情况下进行仿真分析。分析结果显示,本研究给出的粒子群遗传混合优化算法的收敛速度较快,船舶避碰路径较为平滑且路径距离及转向角度都较小,能够同时满足船舶避碰的经济性及安全性要求,相较单一算法具有显著的有效性及高效性。

