船舶推进轴系动力学缩比模型设计
周凌波,熊晨熙,段 勇,吴江海,孙玉东,魏 强,2
(1.中国船舶科学研究中心船舶振动噪声重点实验室,江苏无锡 214082;2.中国舰船研究设计中心,武汉 430064)
0 引 言
船舶推进轴系的作用是将主机的功率传递到螺旋桨,并将螺旋桨的推力传递到船体,推动船舶前进。在船舶推进轴系的三大振动问题——扭转振动、纵向振动和回旋振动中,回旋振动是最为突出的一个难题,关于它的研究,相对于扭转振动和纵向振动的研究来说,不论是在文献发表的数量上还是在研究深度上都是最不够的[1]。水面船舶推进轴系的回旋振动作为造成推进轴系故障的主要原因之一,不仅会严重影响推进轴系的正常运转,导致推进轴系零部件的异常磨损和疲劳破坏,更会激起艉部船体结构的异常振动,产生显著的水下低频、多频强线谱辐射噪声,大大影响水面船舶的声隐身性能[2]。
对于推进轴系回旋振动动力学特性及其控制方法的研究,基于经费、维护和技术上的掣肘,多数仅停留在数值和仿真计算阶段,缺乏有效的试验验证。因此,建造与实船轴系相匹配的缩比轴系回旋振动试验模型,将理论和数值分析与试验测试相结合,显得尤为重要。对于工业转子-轴承系统,国内对其缩比模型及缩比关系已经开展了一定程度的研究[3-5]。船舶推进轴系与工业转子系统虽然具有一定的相似性,但两者的安装基础条件有区别:工业转子系统多安装在刚性基础上,而船舶的推进轴系则是安装在船体结构上。船体结构属于一种弹性支撑,其对于轴系的动力学影响不可忽略。因此,在对船舶推进轴系进行动力学缩比设计时,不仅需要像工业转子一样考虑转轴、轴承、轴承基座的动力学影响,还需要进一步计入船体支撑结构的动力学影响。
本文以某型水面双体船及其推进轴系为原型,计入船体结构的支撑动力学影响,依据动力学参数的缩比换算关系,设计了一种验证轴系回旋振动控制技术的陆上缩比轴系试验模型。然后通过对实船推进轴系和缩比轴系模型的动力学仿真分析和对比,验证了所设计缩比轴系的动力学适用性,为轴系回旋振动控制方法的验证提供了有效的试验对象。
1 缩比换算关系和轴承刚度估算公式
1.1 缩比换算关系
通常设计缩比模型,几何缩比Kl、材料的弹性模型缩比KE和密度缩比Kρ是确定的,因此用这三个基本量可以推导出其他物理量的缩比关系[3],整理列入表1。

表1 缩比模型与原型各物理量间的缩比关系Tab.1 Relationship between the scaled model and the prototype
1.2 轴承刚度计算公式
(1)赛龙轴瓦刚度计算公式为

式中,K1为赛龙轴瓦刚度,E0为压缩模量,L为轴瓦长度,D为轴承直径,t为壁厚。
(2)深沟球轴承径向刚度计算公式为

式中,K2为径向刚度,φ为滚珠直径,F为径向载荷,N为滚子个数,α为接触角。
(3)圆柱滚子轴承径向刚度计算公式为

式中,K3为径向刚度,P为径向载荷,Z为滚子个数,l为滚子有效长度,β为接触角。
2 实船及其推进轴系原型
2.1 设计原型
设计原型以图1所示的某型水面双体船的推进轴系为对象,其船长约为54 m,排水量约为1 400 t。该船推进轴系如图2所示,分为艉轴、中间轴、推力轴三段,总长为15 568 mm,材料为锻钢。其中,艉轴长为8 000 mm,直径为200 mm;中间轴长为4 338 mm,直径为180 mm;推力轴长为3 230 mm,直径为200 mm。艉轴与中间轴之间为套筒式液压联轴器,质量为135 kg;中间轴与推力轴之间为法兰式液压联轴器,质量为143 kg。螺旋桨为6 叶定距桨,材料为镍铝青铜,桨叶和桨毂总质量为1 420.3 kg,转动惯量为363.3 kg·m2。

图1 某型水面双体船Fig.1 Surface catamaran

图2 推进轴系结构组成Fig.2 Structural composition of propulsion shafting
2.2 全船有限元模型
建立的全船有限元模型如图3 所示。船体大部采用板单元建模,转轴与舱室支柱使用梁单元建模,螺旋桨使用三维实体单元建模。主甲板、下甲板和底部船体分段中,T 型加强肋的腹板使用板单元,面板使用梁单元,球扁钢和角钢加强肋统一简化为角钢并用梁单元模拟;主甲板以上船体结构的加强肋则都使用梁单元模拟。船体结构中的烟囱分段、甲板上舷墙分段、稳定鳍加强装置、舭龙骨,导流罩和焊缝等都以分布质量的形式表达。基座部分中位于潜体中的推进电机基座、推力轴承基座、中间轴承基座等按照图纸详细建模,其它没有建模的基座则将其重量分摊到相应的船体主结构上。船上设备,包括油舱和水舱中的质量、发电机组、推进电机、轴承、变压器、变频器、吊架、锚链、前后鳍、舵杆舵叶、交通艇、通风排气系统、锅炉、轮机设备、应急发电机、食品、蓄电池、泵、空调、桅樯等设备的质量,都按照重心加载在给定位置上或者按照质量均匀分布在舱壁上。船上的其它质量,如电缆、油漆等,则按照肋位分布在相应的船体结构上。
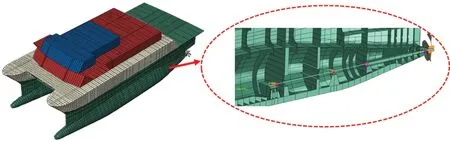
图3 全船有限元模型Fig.3 Finite element model of the whole ship
推进轴系通过艉后轴承、艉前轴承、中间轴承和推力轴承基座与艇体连接。桨毂内表面与转轴采用刚性耦合。螺旋桨采用二次实体单元模拟,轴段采用梁单元模拟,艉后轴承、艉前轴承和中间轴承采用水平和垂向的弹簧单元与船体连接。推力轴承对轴系的纵向运动及横向运动同时具有约束作用,因此在纵向及横向分别采用水平、垂向与纵向的弹簧单元进行模拟。推力盘、联轴器与弹性联轴器则都采用点质量进行模拟。
所建立的船体和推进轴系有限元动力学模型已经过实船航行振动试验的对比验证,两者的动力学特性具有较好的一致性[6]。
2.3 轴承支撑刚度计算
艉后轴承和艉前轴承都属于水润滑动压滑动轴承,轴瓦为赛龙材料。两者对轴系的径向支撑刚度由润滑膜刚度、轴瓦刚度和安装位置的船体刚度三者串联而成[7]。其中,润滑膜刚度采用流体动压润滑理论[8]计算,赛龙轴瓦的刚度根据公式(1)进行计算,其轴承负荷以及安装位置的船体刚度采用有限元法计算。
中间轴承为大比压自润滑白合金轴承,轴承刚度采用CB/Z 208[9]中的推荐值,其轴承负荷以及安装位置的船体刚度采用有限元法计算。
推力轴承的径向支撑部分为双列圆柱滚子轴承,轴承刚度采用公式(3)进行计算,其轴承负荷以及安装位置的船体刚度采用有限元法计算。
各轴承径向负荷、船体基座刚度及总支撑刚度的计算结果如表2、图4和表3所示。

表2 实船各轴承的径向负荷Tab.2 Radial load of each bearing of the real ship
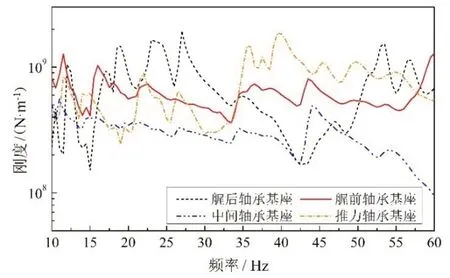
图4 各轴承安装位置处的船体基座刚度Fig.4 Hull base stiffness at each bearing position

表3 实船轴系支撑刚度Tab.3 Support stiffness of the real ship’s shafting
3 缩比轴系模型设计
由于缩比轴系试验模型为在实验室中用于验证回旋振动控制新方法有效性的原理性试验验证模型,因此缩比模型要求设计简单,能反映基本的物理现象,大小满足实验室场地及设备安装要求即可。综合考虑实验室的安装测试条件以及项目的研究经费和研究周期等要求,轴系缩比模型的结构尺寸采用缩尺比例1:4进行设计,并选用密度和弹性模量相近的结构材料,但考虑到实际加工因素,并不要求所有的机械细节参数严格满足缩比要求。
缩比轴系模型的组成主要包括:3 段转轴、4 个支撑轴承、1 个螺旋桨模拟质量盘、2 个刚性联轴器、1个弹性联轴器、1台驱动电机、轴承基座及其他附件等结构。参照实船的布置形式,3段转轴采用刚性联轴器进行连接,艏端与电机输出轴采用高弹性联轴器进行连接。轴系采用4个径向支撑轴承,分别对应实船轴系的后轴承、前轴承、中间轴承以及推力轴承径向支撑。轴系采用直线校中方式进行连接,各轴段的长度、各轴承支撑中心的位置按照实船轴系进行缩比确定,尺寸参数如图5所示。

图5 缩比轴系支撑轴承及联轴器位置Fig.5 Positions of the supporting bearings and couplings of the scaled shafting
本缩比轴系模型主要用于轴系回旋振动控制方法的研究,只产生少量的轴向静态和动态载荷(主要为驱动电机输出轴的轴向窜动力),所以缩比轴系中原推力轴承处主要承受径向载荷,几乎不承受轴向载荷。另外考虑到互换性以及计算和加工方便,支撑轴承均采用同一型号的深沟球轴承。同时考虑到后期控制装置的施加方便,轴承外圈应尽量小。综上考虑,轴承1~4统一选用HRB品牌6011型号的深沟球轴承,其外形及内部的尺寸结构如表4所示。

表4 HRB-6011轴承尺寸参数Tab.4 Parameters of HRB-6011 bearing
采用公式(2)计算各位置轴承处的径向刚度,如表5所示。

表5 缩比轴系各轴承的径向刚度Tab.5 Radial stiffness of each bearing of the scaled shafting
4 缩比轴系和实船轴系动力学仿真对比
分别计算缩比轴系和实船轴系的结构质量、轴承负荷、轴承刚度、横向振动模态频率和加速度传递函数(激励点位于螺旋桨质心处),再根据缩比关系将缩比轴系的计算结果换算为对应实尺度时的结果,并在考核频段10~60 Hz内与实船轴系的计算结果进行对比,如表6~9和图6~8所示。

图6 实船轴系各轴承位置处的传递特性Fig.6 Transmission characteristics of the real ship’s bearings
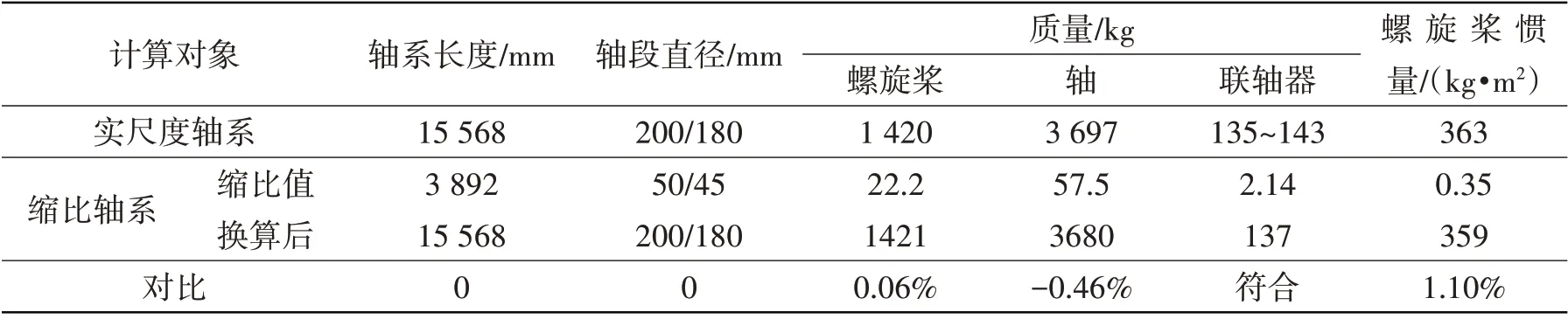
表6 尺寸和结构质量对比Tab.6 Comparison of the dimensions and structural masses
由表6和表7可见,缩比轴系换算后的尺寸与实船轴系一致,结构质量与实船轴系相比最大相差1.10%,轴承负载质量与实船轴系相比最大相差2.12%;由表8 可见,缩比轴系换算后的轴承支撑刚度与实船轴系相比,均处于合理范围内;由表9 可见,缩比轴系换算后的低阶弯曲模态频率与实船轴系相比,最大相差4.93%。
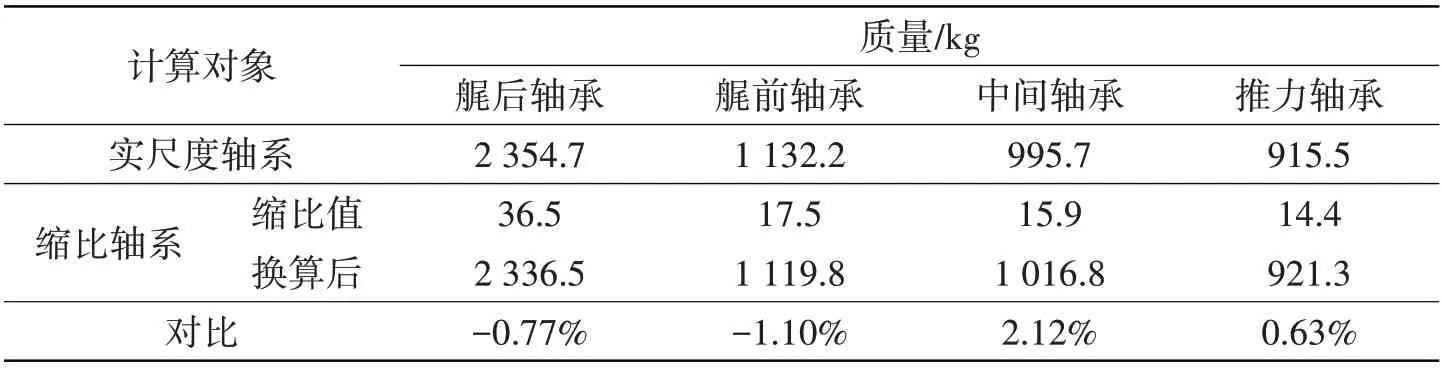
表7 轴承负载质量对比Tab.7 Comparison of the bearings’masses
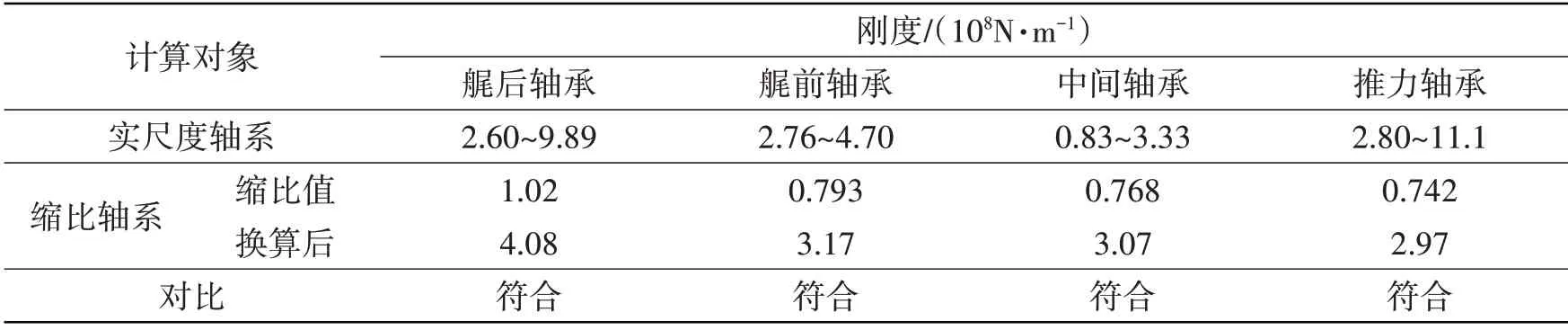
表8 轴承刚度对比Tab.8 Comparison of the bearings’stiffnesses
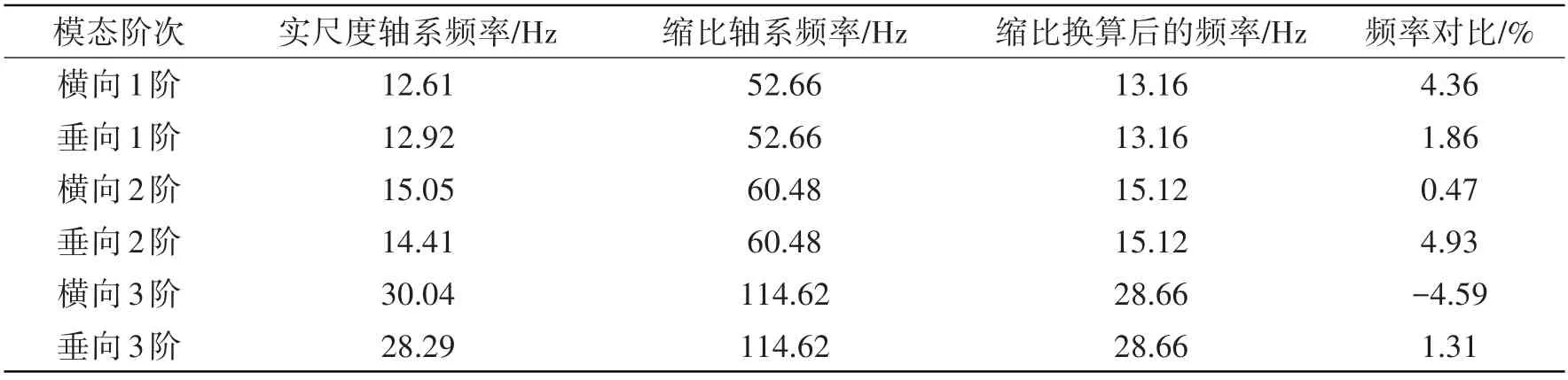
表9 轴系前3阶横向和垂向模态频率对比(换算后)Tab.9 Comparison of the first three lateral and vertical bending modes of the shafting(after conversion)

图7 缩比轴系各轴承位置处的传递特性(换算后)Fig.7 Transmission characteristics of the scaled model’s bearings(after conversion)
由图8 可见,缩比轴系在艉后轴承、艉前轴承、中间轴承以及推力轴承处换算后的动力学传递特性与实船轴系的趋势基本一致,吻合度良好。
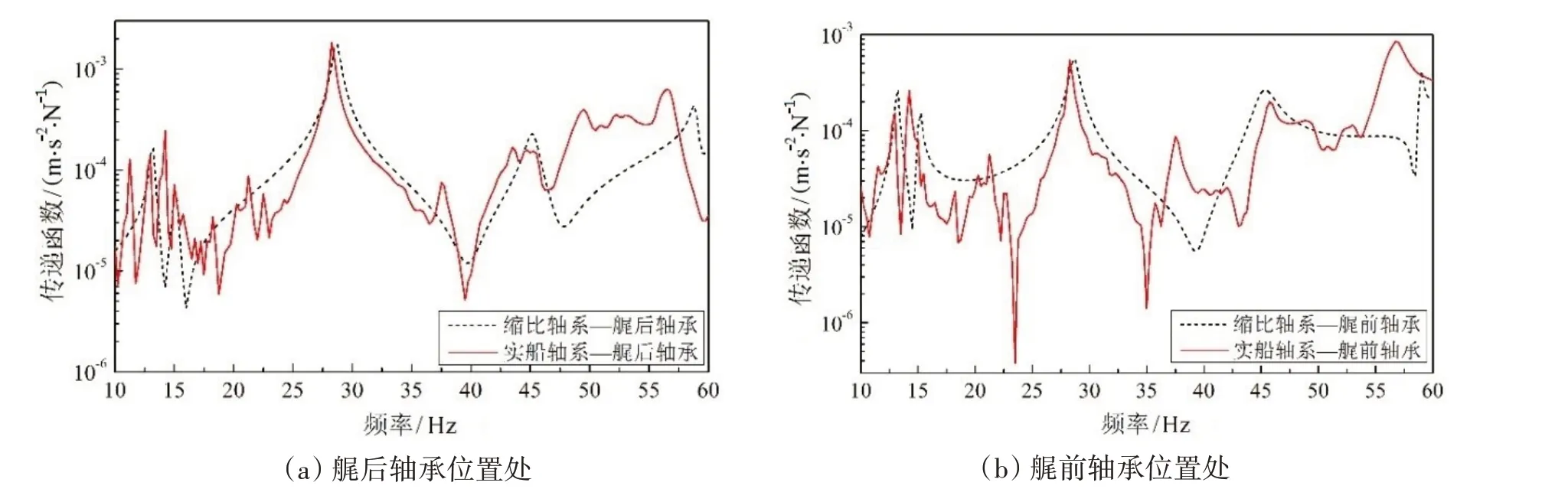
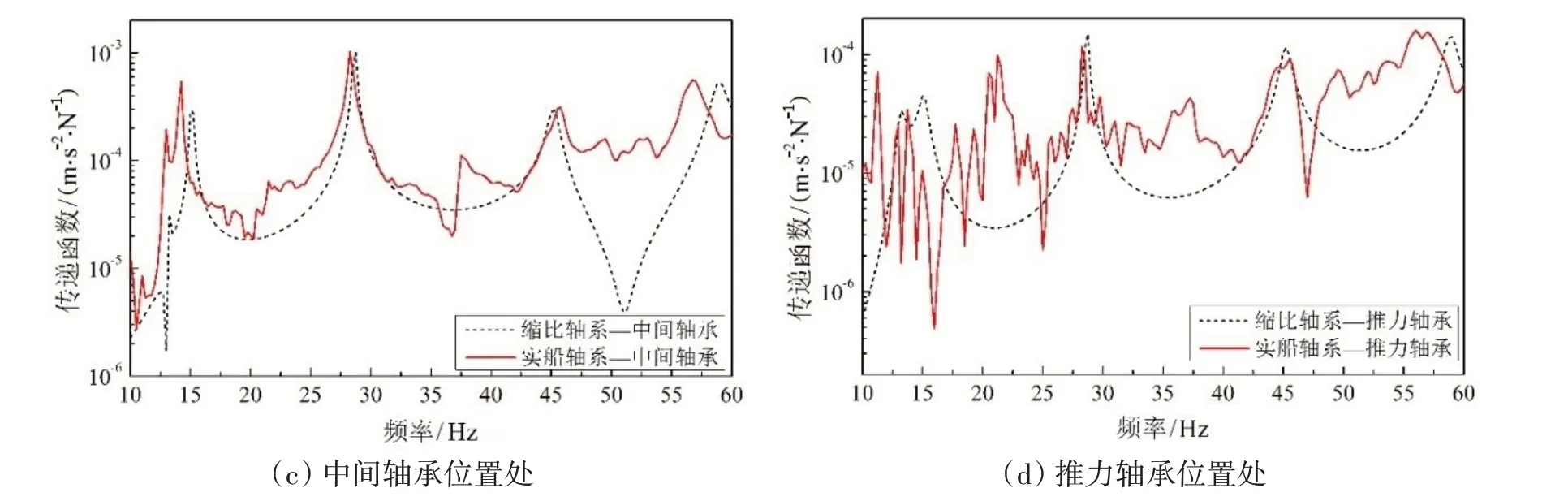
图8 缩比轴系与实船轴系的传递函数对比(换算后)Fig.8 Comparison of the shafting transmission characteristics between the real ship and the scaled model(after conversion)
5 结 语
本文以某型水面双体船及其推进轴系为对象,设计了一种实验室陆上缩比轴系试验模型,并对实尺度模型和缩比模型的动力学特性进行了仿真分析和对比,验证了缩比模型的动力学适用性。由仿真计算结果对比可见,缩比轴系换算后的轴承负载质量与实船轴系相比,最大相差2.12%;缩比轴系换算后的轴承支撑刚度与实船轴系相比,均处于合理范围内;缩比轴系换算后的低阶弯曲模态频率与实船轴系相比,最大相差4.93%;缩比轴系在艉后轴承、艉前轴承、中间轴承以及推力轴承处的传递规律与实船轴系的趋势基本一致,吻合度良好。
因为实船的船体结构和轴系结构较缩比轴系复杂许多,除了轴系自身振动模态的参与外,还有许多的船体结构局部振动模态和耦合振动模态参与动力学传递,因此实船轴系的传递频点较缩比轴系丰富,动力学传递特性也较缩比轴系复杂,很难实现完全一致。同时,受限于实验室场地条件和其它客观因素,缩比轴系在设计时做了一定的合理简化(如并不附加船体结构、将螺旋桨简化为质量圆盘、将滑动轴承简化为滚动轴承等),因此其动力学特性与实船并不完全一致。但由文中动力学对比结果可见,两者在考核频段内的动力学传递特性吻合度良好,所以认为设计的该缩比轴系能够满足使用要求。

