耐压圆柱壳体的临界失稳压力预测
于 波,刘军鹏,张博文,徐 蒙,邱中梁,段梦兰
(1.中国石油大学安全与海洋工程学院,北京 102249;2.中国船舶科学研究中心,江苏无锡 214082)
0 引 言
耐压壳体结构是深潜器、水下空间站、水下航行器等装备的重要组成部分,主要有圆柱壳[1]、球壳[2]以及各种组合壳[3]等型式。圆柱壳由于几何结构简单,制造加工相对比较容易,已逐渐发展成为最常见的水下耐压壳结构,其在外压工程环境下失效形式主要有两种:强度破坏和屈曲失稳,强度破坏主要是材料达到了屈服强度而发生了塑性变形,屈曲失稳是指耐压结构失去稳定性而丧失承载外压能力的过程。在实际工程中,圆柱壳屈曲失效的概率要远远大于强度破坏,且屈曲失稳常在无明显征兆的情况下突然发生[1]。因此,围绕圆柱壳体结构的屈曲问题,进行极限承载力的预测具有重要的科学和工程意义。
屈曲问题本质上属于非线性理论范畴,目前解决屈曲问题的方法主要有静力学法、能量法以及数值试验法,三种方法的区别和联系列于表1。
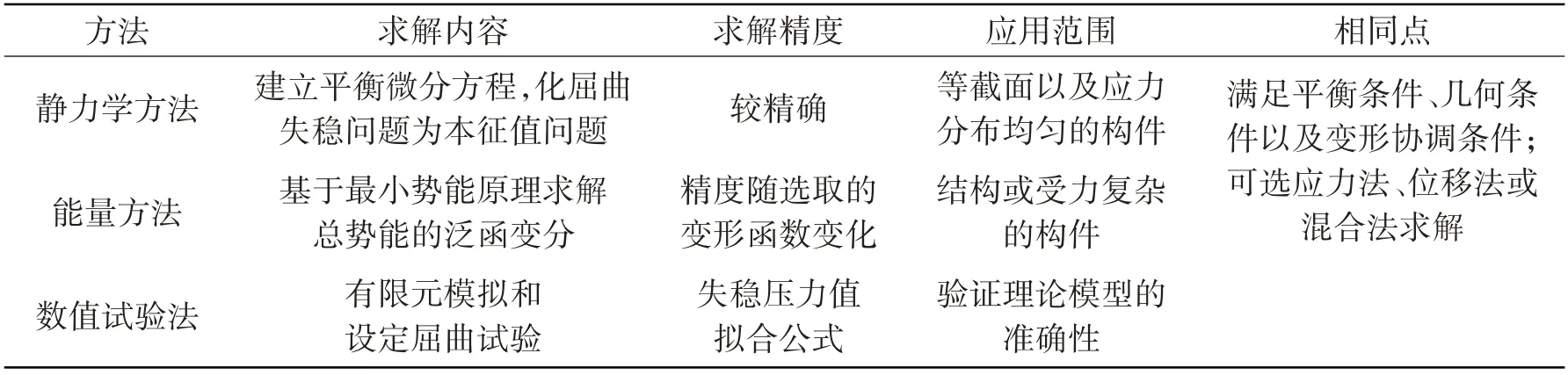
表1 三种求解方法的区别和联系Tab.1 Differences and connections among three solutions
基于以上三类方法,国内外学者分别从不同的角度对圆柱壳的屈曲稳定性问题进行了研究,并取得了重要的研究成果。von Mises 依据小挠度理论,给出了简支边界条件下薄壁圆柱壳在均匀侧向外压和轴向压力作用下的圆柱壳失稳压力公式:

式中,E为弹性模量,μ为泊松比,t为圆柱壳壁厚,a为半径,l为轴向长度,n为周向失稳波数,可通过选取合适的周向失稳波数n来得到Pcr的最小值[4]。Nash 采用能量法详细计算了固支边界条件下薄壁圆柱壳在静水外压作用下的临界失稳压力值,结果与已知结论非常接近[5]。Pinna等[6]使用能量法研究了不同边界条件下圆柱壳在静水外压作用下的屈曲问题,研究发现,对于中等长度的圆柱壳体,不同边界条件下的失稳压力可通过对壳体约束端施加标量乘子α来确定。
在数值试验研究方面,Aghajari等[7]进行了圆柱形钢壳试样在外压作用下的压溃试验,发现试验结果与有限元结果较为一致。江苏科技大学的朱永梅团队对不同长径比的304不锈钢圆柱壳进行了外压下的屈曲试验,同时进行了不同长径比下外压圆柱壳的数值模拟,最终发现实验结果与有限元结果的偏差为2%~9%[8]。
中国船级社CCS2013[9]中给出了圆柱壳的临界失稳压力经验公式:

美国船级社ABS2012[10]也给出了计算圆柱壳临界失稳压力的经验公式:
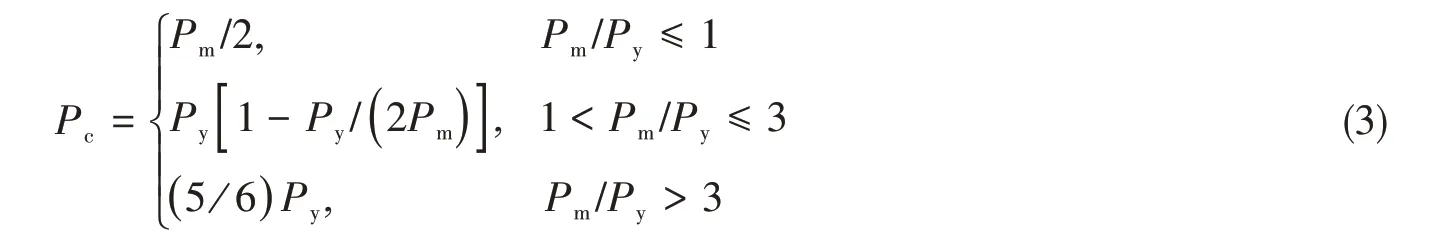
式中,Py是屈服载荷,Pm是von Mises失稳压力。
可以发现,前人采用的分析方法属于拉格朗日解算系统,可通过应力法或者位移法进行求解,许多重要的基本结果可以从线性的小挠度理论来获得,但在有关结构稳定性试验中发现壳体的失稳压力与线性理论解相差较大[11],主要是因为理论分析时,存在大量的假设条件,且并未考虑初始几何缺陷值以及材料的非线性等因素。经验公式虽然能很好地指导实际工程项目,但由于基于工程经验而引入了大量的修正系数使得临界失稳压力产生较大的误差。因此本文拟在减少假设条件的基础上,利用静力学方法建立圆柱壳的临界失稳压力预测模型,同时建立数值模型,该模型考虑初始几何缺陷和材料的非线性因素,最后将理论模型与数值模型分别和试验结果及前人模型进行比较,证明本文模型的合理性和先进性。
1 理论模型
1.1 基本假设
前人在利用静力法求解圆柱壳的应变—位移几何关系时,基于不同的假设条件得到了不同的应变—位移关系表达式,因此,有必要对相关假设条件进行归纳整合:
(1)中面的法线在变形过程中保持不变,满足直法线假设;
(2)对于壳体的运动学关系,假设从中面到任一点的距离z不受壳体变形的影响,并忽略z方向的应力σz;
(3)所有的位移都很小,满足小变形假设;
(4)前屈曲状态为薄膜无矩状态,不考虑屈曲前的弯曲等因素的影响。
依据整合后的假设条件推导圆柱壳任意一点的应变—位移几何关系。
1.2 推导过程
根据文献[12]的内容,可得圆柱壳中面的应变—位移关系式为

针对圆柱壳内任一点的应变—位移关系,在圆柱壳横剖截面上采用微元法(图1)进行位移关系的分析。A为圆柱壳体半径为r的中线上一点,其环向和径向位移的变化分别为v和w;B为壳体内距离中线为z的任意一点,且z<t/2,t为圆柱壳厚度,其环向和径向位移变化分别为vB和wB。

图1 圆柱壳横剖截面微元体Fig.1 Microelement body of cross section of cylindrical shell
由微元体图可以看出,弧长vx与A点的环向位移v有相同的圆心角,计算可得
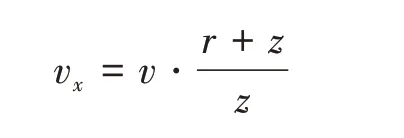
圆柱壳体变形过程中中线的偏转角为β,同理可得
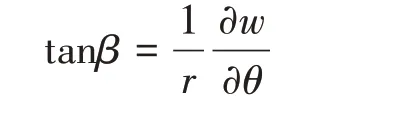

同理,在纵剖截面上(图2)对位移关系进行分析:
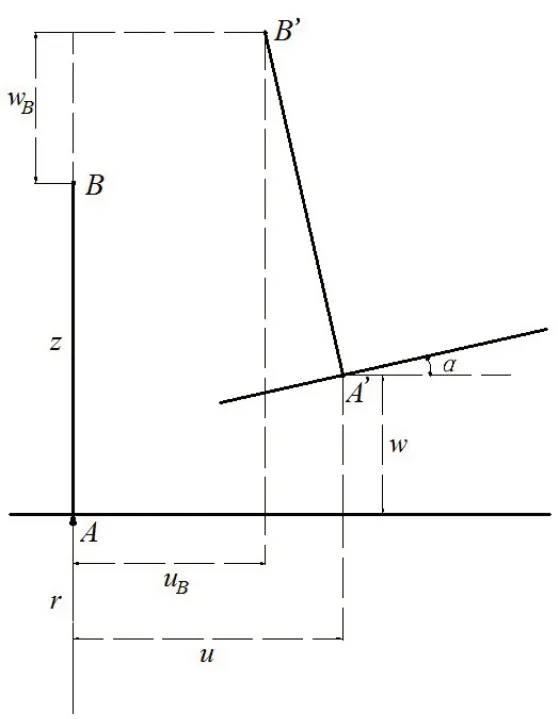
图2 圆柱壳纵剖截面微元体Fig.2 Microelement body of longitudinal section of cylindrical shell
图中,A点轴向和径向位移的变化分别为u和w;B点环向和径向位移变化分别为uB和wB,根据微元体几何关系,有

对于B点的径向位移wB,综合考虑圆柱壳体纵剖面和横剖面的相关几何关系,则有

为了得到壳体上任一点B的应变—位移关系,将B点的位移uB、vB和wB代替中面的位移u、v、w,同时将B点的半径r+z代替中面的半径r,得到圆柱壳任一点的应变—位移关系表达式
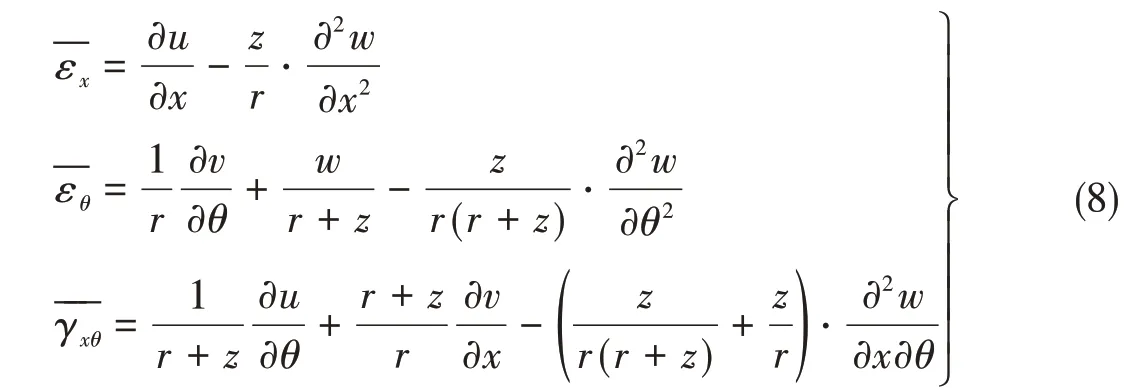
根据胡克定律,可得

壳体的内力和内力矩分别为各项应力在壳体横截面上沿厚度方向的积分,则有


引入圆柱壳失稳时的轴向、环向以及径向的位移函数:

式中,U、V和W为任意常数,λ=mπ/L,L为圆柱壳的长度,m为圆柱壳屈曲轴向半波数,n为环向波数。
分析位移函数可以发现,当x=0 和x=L时,v=w=0,u≠0。因此可得圆柱壳的边界条件为:两端切向与径向位移被限制,轴向方向没有施加约束。
最终可得齐次线性方程组:

由此,采用静力学方法将圆柱壳的屈曲失稳问题转化为本征值问题,求解圆柱壳的临界失稳压力,要保证方程组有非零解,即其系数行列式为零:

式中,

赋予圆柱壳相关几何参数,假设不同的失稳波数m和n值,就可以得到对应的圆柱壳的失稳压力,将失稳压力值用对数形式表示,结果如图3 所示。在由(m,n)的不同组合求出的失稳压力中,选取最小的那个失稳压力,即为圆柱壳的临界失稳压力Pcr,对应的(m,n)值就是临界失稳波数,从图3中可以看出,此圆柱壳的临界失稳波数是m=1,n=3,对数坐标下结果值为-0.039,实际的临界失稳压力为0.914 MPa。

图3 不同失稳波数下的圆柱壳失稳压力Fig.3 Instability pressure of cylindrical shell under different instability wave numbers
2 数值模型
分别建立不同长径比的圆柱壳有限元模型,尺寸参数列于表2。

表2 不同长径比的圆柱壳尺寸Tab.2 Cylindrical shell sizes with different aspect ratios
圆柱壳采用304 不锈钢材料,E=176.05 GPa,μ=0.25,σs=323.18 MPa。分析中,设置外压为P0=1 MPa,作用在圆柱壳整个外表面,边界条件为:两端周向和径向位移被限制,轴向方向没有约束,即
U1=U2=UR3=0,U3≠0
Riks弧长分析法可以追踪壳体结构的非线性平衡路径,获得壳体结构的载荷—位移曲线,并且可以评估壳体的真实临界失稳压力和后屈曲行为[13]。本文采用特征值屈曲—Buckle 算法以及非线性屈曲—弧长分析法进行圆柱壳的屈曲研究。
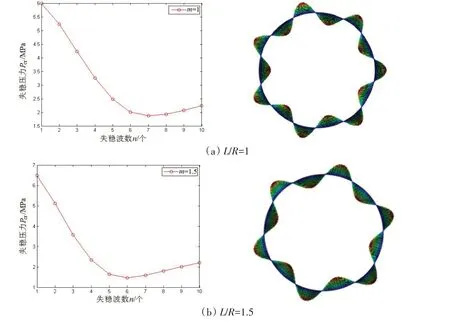
特征值屈曲分析中,进行了不同长径比下的圆柱壳模态分析,将其与理论推导出的最小失稳波数进行了对比,如图4所示。弧长分析法中,考虑材料的非线性影响,引入由304不锈钢真实应力和真实应变确定的材料塑性参数;对于初始几何缺陷,常将线性屈曲的第1阶本征模态作为最坏几何缺陷引入。对于薄壳结构,缺陷幅值一般取为1%~10%的壳体厚度,为了探究不同初始缺陷幅值对临界失稳压力的影响规律,建立不同缺陷值下的圆柱壳模型,进行了有限元验证,结果如图5 所示。其中,横坐标代表不同壁厚百分比下的初始缺陷幅值,纵坐标代表圆柱壳的临界屈曲值。可以发现,当初始缺陷幅值增大到壳体厚度的10%后,临界屈曲值变化趋于平缓,故缺陷幅值定为10%的壳体厚度,最终可以得到圆柱壳的平衡路径,如图6 所示,仅提供长径比为1.5 情况下的结果。

图4 不同长径比下的失稳波数对比Fig.4 Comparison of instability wave numbers under different aspect ratios

图5 初始缺陷幅值对临界失稳压力的影响Fig.5 Effect of initial defect amplitude on critical buckling load
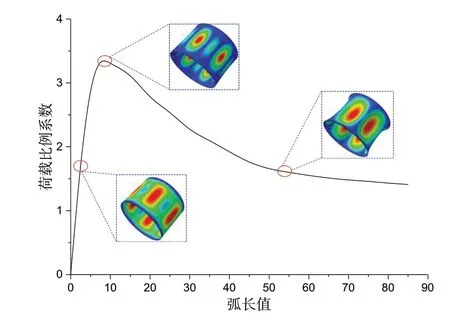
图6 圆柱壳的非线性屈曲平衡路径Fig.6 Nonlinear buckling equilibrium path of cylindrical shell
可以看出,随着弧长值的增加,荷载几乎呈线性增加,直至达到临界失稳压力3.401 MPa,超过该峰值,荷载急剧下降,随后缓慢下降。同理,可以得到其他长径比下的结果,见图7。
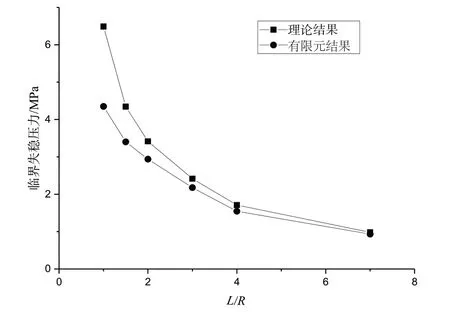
图7 理论结果与有限元结果对比图Fig.7 Comparison between theoretical results and finite element results
由图可知,在圆柱壳长径比较小时,理论结果与有限元模拟结果存在一定的误差,随着长径比的不断增大,理论值与有限元结果逐渐趋于吻合。
3 案例分析与讨论
为了验证理论结果与有限元模拟结果,本文取江苏科技大学朱永梅团队[8]的304不锈钢圆柱壳的耐压试验作为对比验证,E=176 050 MPa,μ=0.25,σs=323.15 MPa,试验相关数据列于表3。表中最后一列是换算之后的圆柱壳中面半径r中。
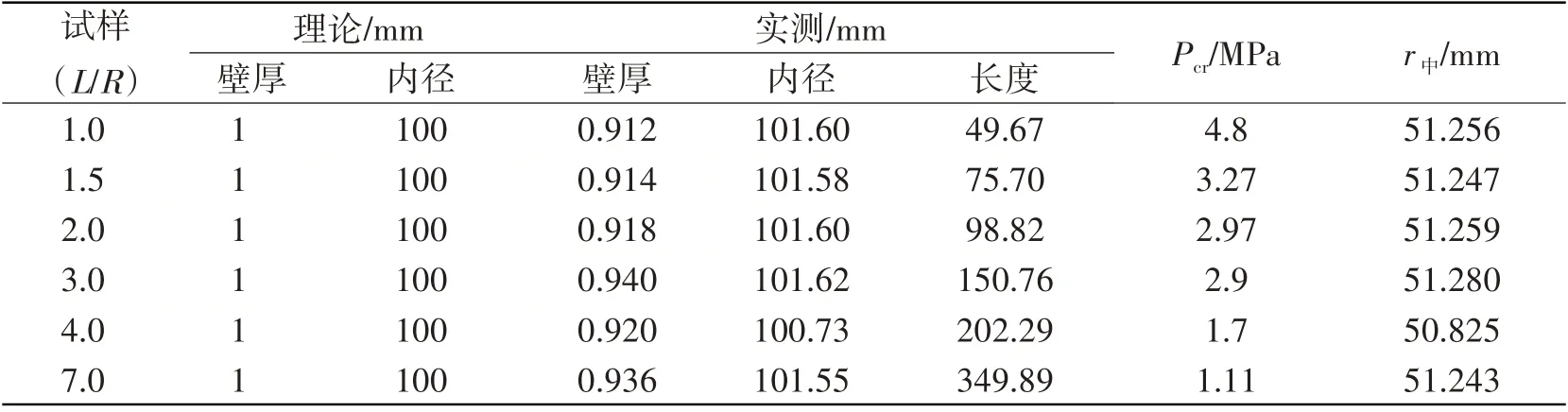
表3 试验相关数据Tab.3 Relevant data of the experiment
将试验结果分别与理论结果以及有限元结果进行了对比,如图8 所示。由图8 可以看出,试验结果在L/R=3 时存在异常,不作分析讨论。三条结果曲线在L/R较小时差别较大,随着L/R的增大,三条曲线趋于吻合,并对此进行了误差的定量分析。

图8 不同长径比下的理论、试验与有限元结果对比Fig.8 Comparison among theoretical,experimental and finite element results under different aspect ratios
由图9 可以看出,试验结果与理论结果在L/R较小时,误差值较大,且在L/R=1 时,误差值达到30%,随着L/R的不断增大,误差值逐渐减小,在L/R=4 时,误差值降为0.6%。试验结果与有限元模拟结果的误差曲线较为平缓,误差值基本都在10%以内,试验结果能很好地验证有限元的模拟结果。同时可以发现,当L/R值较小时,数值模拟结果更加贴近试验结果,而当L/R值较大时,理论模型则更具优势。
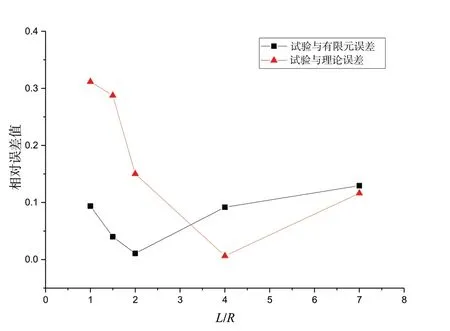
图9 不同长径比下试验与理论、有限元结果的误差Fig.9 Errors of experimental and theoretical and finite element results under different aspect ratios
运用静力学方法求解圆柱壳的临界失稳压力时,会涉及到求解应变—位移几何关系,Flügge[12]、Donnel[14]和Kraus[15]分别基于一定的理论及假设得到了相应的几何关系表达式。为了更进一步证明理论结果的准确性,本文基于不同的几何关系表达式,得到了不同的临界失稳压力,将其与理论结果进行了比较,如图10 所示。
由图10 可以看出,相比于其他理论结果,本文理论模型得到的临界失稳压力更为贴近试验结果,虽然在长径比较小时仍存在一定的误差,但误差值低于30%,且随着长径比的增大,理论解能很好地预测试验结果。
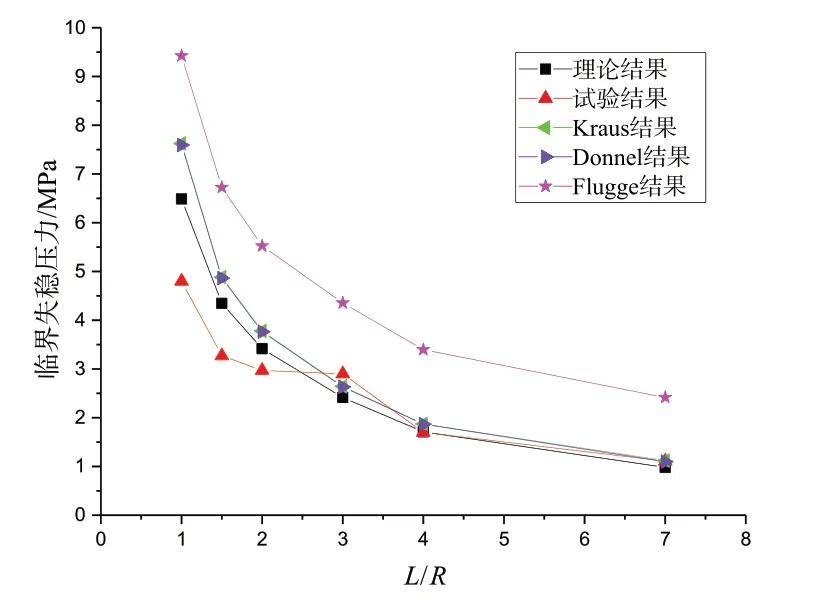
图10 理论结果与其他模型结果的比较Fig.10 Comparison of theoretical results with results from other models
4 结 语
本文针对圆柱壳的屈曲失稳问题,总结了分析屈曲问题的常用方法:静力学方法、能量法以及数值试验法,并指出了其在分析过程中存在的局限性。本文基于整合后的假设条件,运用微元法,推导了圆柱壳任意一点的应变—位移关系式,继而应用静力学方法,将圆柱壳的屈曲失稳问题化为求解方程组的特征值问题,根据稳定性条件求解系数行列式为零的解,最终得到了圆柱壳的最小失稳波数以及对应的临界失稳压力。
为了验证理论推导出的圆柱壳临界失稳压力,本文利用有限元软件ABAQUS 对长径比为1~7 的不同圆柱壳进行了屈曲模拟,进行特征值屈曲分析时,在相同的边界条件下,得到了圆柱壳的一阶屈曲模态值与理论计算的最小失稳波数一致的结论;进行弧长分析时,验证了初始几何缺陷幅值对圆柱壳临界失稳压力的影响规律,根据规律将缺陷幅值取为壳体壁厚的10%,得到了圆柱壳的临界失稳压力值。同时,通过对比得到临界失稳压力的理论结果与有限元结果的偏差为4%~32%,且随圆柱壳长径比的增大而减小,有限元结果较好地验证了圆柱壳理论屈曲解的正确性。
通过将理论计算结果和有限元模拟结果与试验结果对比发现,在长径比较小情况下数值模型结果更加贴近试验结果,但在长径比较大情况下,本文给出的理论模型结果则与试验结果更加吻合。在长径比为1的情况下,数值模型和理论模型的结果均与试验结果存在一定的误差,这还有待进一步研究。

