2021年新高考全国I卷第21题的探究

广东省佛山市乐从中学(528315)林国红

一、题目呈现

题目(2021年新高考全国I 卷第21 题)在平面直角坐标系xoy中,已知点点M满足|MF1|−|MF2|=2,记M的轨迹为C.

(1)求C的方程;

(2)设点T在直线上,过T的两条直线分别交C于A,B两点和P,Q两点,且|TA|·|TB|=|TP|·|TQ|,求直线AB的斜率与直线PQ的斜率之和.

试题主要考查双曲线的定义及标准方程,直线方程,直线与圆锥曲线的位置关系,圆锥曲线中的定值问题等;解题思想方法方面主要考查转化与化归,数形结合等思想.综合考查考生逻辑思维、推理论证及运算求解等方面的能力,试题的思维过程和运算过程体现了能力立意的思想,较好地体现了解析几何中核心内容和基本思想方法的考查.本题对于考生运用所学知识,寻找合理的解题策略以及推理论证和运算能力有较高的要求.

由于问题(1)较为简单,本文不作讨论,下面对问题(2)进行解答与探究.

二、解法探究

评注本解法的运算量虽不小,但方法是解析几何中的常用方法,这种通性通法在数学解题中有重要作用.所以在平时的教学中要注重一般性的解题规律和方法(即通性通法),要重视知识的生成过程,尽量创设问题情境引导学生探究知识,培养学生分析问题、解决问题的能力.

三、问题的提出

经过解后反思,我们提出如下问题:

问题1在试题的问题(2)中,直线改为x=m,直线AB的斜率与直线PQ的斜率之和为多少?

问题2在试题的问题(2)中,若将双曲线一般化,直线AB的斜率与直线PQ的斜率之和为多少?

问题3在试题的问题(2)中,若将双曲线改为椭圆或抛物线,结论是否有变化?

四、试题的背景探析

要回答上述问题,可以从试题的命题背景进行分析.

1 圆幂定理

圆幂定理是平面几何中的一个重要定理,是相交弦定理、切割线定理、割线定理的统称.

(1)相交弦定理 圆内的两条相交弦,被交点分成的两条线段长的积相等.

(2)切割线定理 从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.

(3)割线定理 从圆外一点P引两条割线与圆分别交于A,B;C,D,则有PA·PB=PC·PD.

2 圆幂定理的逆定理

(1)两条线段AB和CD交于点P,若PA·PB=PC·PD,则A,B,C,D四点共圆.

(2)共端点P但不共线的两条射线上有两点A,B和C,D,若PA·PB=PC·PD,则A,B,C,D四点共圆.

(3)共端点P但不共线的两条射线,其一条上有两点A,B,另一条上有一点C,若满足PA·PB=PC2,则圆ABC和射线PC相切于点C.

圆幂定理多用来解决线段的乘积式与比例式相关的问题,而圆幂定理的逆定理多用来解决四点共圆以及圆与直线相切的问题.

3 二次曲线中的四点共圆

结论1若两条直线与二次曲线Γ:ax2+by2+cx+dy+e=0(ab)有四个交点,则这四个交点共圆的充要条件是这两条直线的斜率均不存在或这两条直线的斜率均存在且互为相反数.

由于两条直线的斜率均不存在的情形较为简单,下面中只对两条直线的斜率均存在的情形进行证明.

证明设两条直线li:y−y0=ki(x−x0)(i=1,2),由l1,l2组成的曲线为C:[y−y0−k1(x−x0)]·[y−y0−k2(x−x0)]=0.从而,经过C与Γ 的四个交点的二次曲线一定能表示成以下形式(λ,µ不同时为0):

必要性若四个交点共圆,则存在λ,µ使方程①表示圆,故方程①左边展开式含xy项的系数−µ(k1+k2)=0.当µ=0 时,方程①表示曲线,不表示圆,从而µ0.所以k1+k2=0.

充分性当k1+k2=0 时,方程①左边的展开式是不含xy的项,取µ=1 时,令方程①左边的展开式中含x2,y2项的系数相等,即得.将µ=1,代入①,整理得

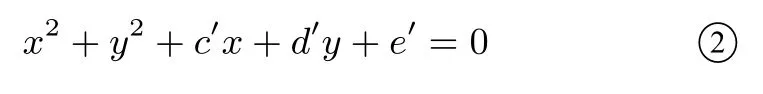
方程②所表示的曲线有且仅有三种情形:一个圆,一个点,无轨迹.因为四个交点在曲线②上,故方程②表示圆.所以四点共圆.

综上,结论1 得证.

结论2若两条直线与二次曲线Γ:ax2+by2+cx+dy+e=0(ab)有四个交点,则这四个交点共圆的充要条件是这两条直线的倾斜角互补.

结论2 的证明可参照结论1 的证明过程,详细的证明过程不再赘述.显然,试题是以圆幂定理的逆定理及结论1 为背景命制的:因为|TA|·|TB|=|TP|·|TQ|,由圆幂定理的逆定理,可得A,B,P,Q四点共圆.且直线AB,PQ存在斜率,由结论1,即得直线AB的斜率与直线PQ的斜率之和为0.另外,从上述分析可知,试题的结论对于椭圆或抛物线也成立,具有一般性,这也解答了上文给出的三个问题.

五、追本溯源

人教A 版数学选修4-4《坐标系与参数方程》第38 页例4 及其变式.

例4 如图,AB,CD是中心为点O的椭圆的两条相交弦,交点为P.两弦AB,CD与椭圆长轴的交角为∠1,∠2,且∠1=∠2.求证:|PA|·|PB|=|PC|·|PD|.

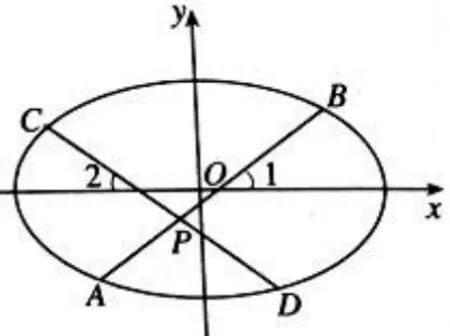
变式探究 把椭圆改为双曲线,是否会有类似的结论?

问“题”那得清如许,唯有源头活水来,可以看出今年考题问题(2)的“母题”来源于课本的例题,高考题只是将例题进行适当的改编,赋于更丰富的知识而已.立足教材,选编教材原题,生成教材变题,是高考命题的一个不争的事实,这体现了高考命题的公平性和基础性原则.因此,高三的数学复习应立足于教材,钻研教材,深刻领悟教材中数学知识的作用和蕴含的人文素养价值;活用教材,对教材中有潜在本质规律的材料、例题、习题进行归纳、类比、拓展,充分挖掘,将其价值发挥出来,从而实现教材教学功能的最大化、最优化.

六、高考与竞赛链接

圆具有丰富的几何性质,它与圆锥曲线之间有着千丝万缕的内在联系.圆的性质的应用是近几年高考命题中体现“在知识交汇点设计问题”这一思路的良好素材,倍受命题者青睐,也应引起我们足够的重视.为了凸现考题的有迹可循,把握复习的侧重点,提高复习效率,下面给出部分相关的高考与竞赛试题,以供参考.

1.(2002年高考江苏卷第20 题)设A,B是双曲线上的两点,点N(1,2)是线段AB的中点.

(1)求直线AB的方程;

(2)如果线段AB的垂直平分线与双曲线相交于C,D两点,那么A,B,C,D四点是否共圆?为什么?

2.(2005年高考湖北卷理科第21 题)设A,B是椭圆3x2+y2=λ上的两点,点N(1,2)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C,D两点.

(1)确定λ的取值范围,并求直线AB的方程;

(2)试判断是否存在这样的λ,使得A,B,C,D四点在同一个圆上?并说明理由.

3.(2011年高考全国I 卷理科第21 题)已知O为坐标原点,F为椭圆C:在y轴正半轴上的焦点,过F且斜率为的直线l与C交于A,B两点,点P满足.

(1)证明:点P在C上;

(2)设点P关于点O的对称点为Q,证明A,P,B,Q四点在同一圆上.

4.(2014年高考全国卷理科第21 题)已知抛物线C:y2=2px(p >0)的焦点为F,直线y=4 与y的交点为P,与C的交点为Q,且.

(1)求C的方程;

(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线l′与C相交于M,N两点,且A,M,B,N四点在同一圆上,求l的方程.

(1)求椭圆E的方程;

(2)设不过原点O且斜率为的直线l与椭圆E交于不同的两点A,B,线段A,B的中点为M,直线OM与椭圆E交于C,D.证明:|MA|·|MB|=|MC|·|MD|.

6.(2009年高中数学联赛江苏省复赛第3 题)已知抛物线y2=2x及点P(1,1),过点P的不重合的直线l1,l2与此抛物线分别交于点A,B,C,D.证明:A,B,C,D四点共圆的充要条件是直线l1与l2的倾斜角互补.

7.(2014年高中数学联赛湖北省预赛第12 题)设A,B是双曲线上的两点,点N(1,2)是线段AB的中点,线段AB的垂直平分线与双曲线相交于C,D两点.

(1)确定λ的取值范围;

(2)试判断A,B,C,D四点是否共圆?并说明理由.

七、结束语

高考试题是精心之作,每年的高考题在命题角度、题型、难度等方面都进行了充分考虑,是知识、能力和思想方法的载体,具有典型性、示范性和权威性.高考试题除了具有测试与选拔功能外,还具有良好的教学功能,要了解高考动向、把握高考脉搏,高考试题的研究是重要的路径.

数学教育家波利亚曾说:与其穷于应付繁琐的数学内容和过量的题目,还不如适当选择某些有意义的题目去帮助学生发掘题目的各个方面,在指导学生解题的过程中,提高他们的才智与推理能力.所以教师对要对高考试题做深入的分析与研究,要跳入题海多做题多思考,才能做到融会贯通、信手拈来,并帮助学生跳出题海.对高考试题的深度探究,不仅使教师清晰地理解命题人的思想、命题背景和考查目的,还可以更好地培养学生思维品质,提高学生提出问题、分析问题和解决问题的能力,从而提高学生的数学核心素养.