结论不同,孰是孰非——对一道高三模拟试题的解法探究

陕西省汉中市教研室(723000)冯云

数学解题犹如打仗,解题者的兵力就是数学基础知识,解题者的兵器就是数学基本思想方法,然而要打胜仗,即正确的解决数学问题,不仅需要解题者对数学知识与思想方法的深刻理解,还需要注重细节、逻辑严密等,否则就会不可避免的出现一些似乎很“正确”的错误.

笔者在2021年全市高三调研过程中,就发现了一些似乎很“正确”的错误,现整理成文,希望能起到一定的警示作用,并供高三师生复习备考时选用.

一、试题呈现

题目已知f(x)=ax−lnx.

(1)讨论函数f(x)的单调性;

(2)若f(x+1)>a对任意x∈[1,2]恒成立,求参数a的取值范围.

二、错解展示

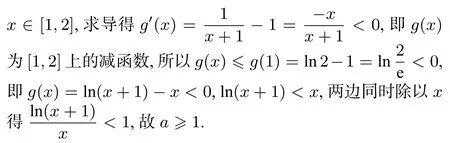
三、错因分析

上述解法一、二、三都是错误的,详细理由如下:

解法一错因不等式ln(x+1)≤x的几何解释如下图1:

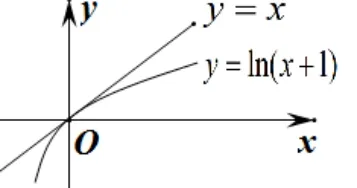
图1

显然,当且仅当x=0 时,取等号,然而x=0 /∈[1,2],即“等号”取不到,从而导致了参数a的范围错误.

解法二错因 将g(x)>h(x)恒成立转化为g(x)min>h(x)max时,当两函数的最大值与最小值在同一自变量处取得时,是正确的,如图2所示.

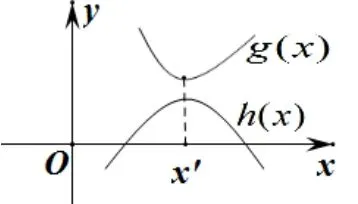
图2

然而,当两函数的最大值与最小值不在同一自变量处取得时,将g(x)>h(x)恒成立转化为g(x)min>h(x)max是不等价的,如图3所示.

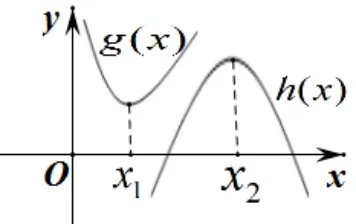
图3

四、正确解法

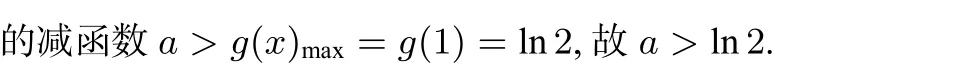
点评上述正确解法主要通过变参分离后,将恒成立问题转化为函数最值问题,然而两次构造函数是此解法的难点所在.

在日常的数学学习中,学生解答出错并不可怕,重要的是要有辨析错误的能力和改正错误的勇气,错解是一种重要的学习资源,应该善于剖析错误,找到错误的根源,加深对数学基本知识与技能的掌握程度,挖掘题目的数学本质,从而锻炼自己的数学意志品质,提高学生辨别错误和解决问题的能力,促进学生数学素养与创新能力的发展.